Extended Set of Coefficients of a Logistic Growth Model — extcoef

Estimate model-specific derived parameters of the logistic growth model

Usage

extcoef_logistic(object, quantile = 0.95, time = NULL, ...)

Arguments

object: model object fited by fit_growthmodel
quantile: fraction of the capacity parameter (K) for the quantile method
time: 2-valued vector of the search interval for the independent variable (time). Note: this needs to be set this manually if saturation is not reached within the observation time period taken from the data.
...: reserved for future extensions

Value

vector that contains the fitted parameters and some derived characteristics (extended parameters) of the logistic function.

Details

This function returns the estimated parameters of a logistic growth model (y0, mumax, K) and a series of estimates for the time of approximate saturation. The estimates are defined as follows:

turnpoint: time of turnpoint (50% saturation)
sat1: time of the minimum of the 2nd derivative
sat2: time of the intercept between the steepest increase (the tangent at mumax) and the carrying capacity K
sat3: time when a quantile of K (default 0.95) is reached

This function is normally not directly called by the user. It is usually called indirectly from coef or results if extended=TRUE.

Note

The estimates for the turnpoint and the time of approximate saturation (sat1, sat2, sat3) may be unreliable, if saturation is not reached within the observation time period. See example below. A set of extended parameters exists currently only for the standard logistic growth model (grow_logistic). The code and naming of the parameters is preliminary and may change in future versions.

Examples


## =========================================================================
## The 'extended parameters' are usually derived
## =========================================================================

data(antibiotic)

## fit a logistic model to a single data set
dat <- subset(antibiotic, conc==0.078 & repl=="R4")

parms <- c(y0=0.01, mumax=0.2, K=0.5)
fit <- fit_growthmodel(grow_logistic, parms, dat$time, dat$value)
coef(fit, extended=TRUE)
#>          y0       mumax           K   turnpoint        sat1        sat2 
#>  0.01505667  0.40193712  0.45220395  8.38053668 11.65706694 13.35643933 
#>        sat3 
#> 15.70615819 

## fit the logistic to all data sets
myData <- subset(antibiotic, repl=="R3")
parms <- c(y0=0.01, mumax=0.2, K=0.5)
all <- all_growthmodels(value ~ time | conc,
                         data = myData, FUN=grow_logistic,
                         p = parms, ncores = 2)


# par(mfrow=c(3,4))
plot(all)












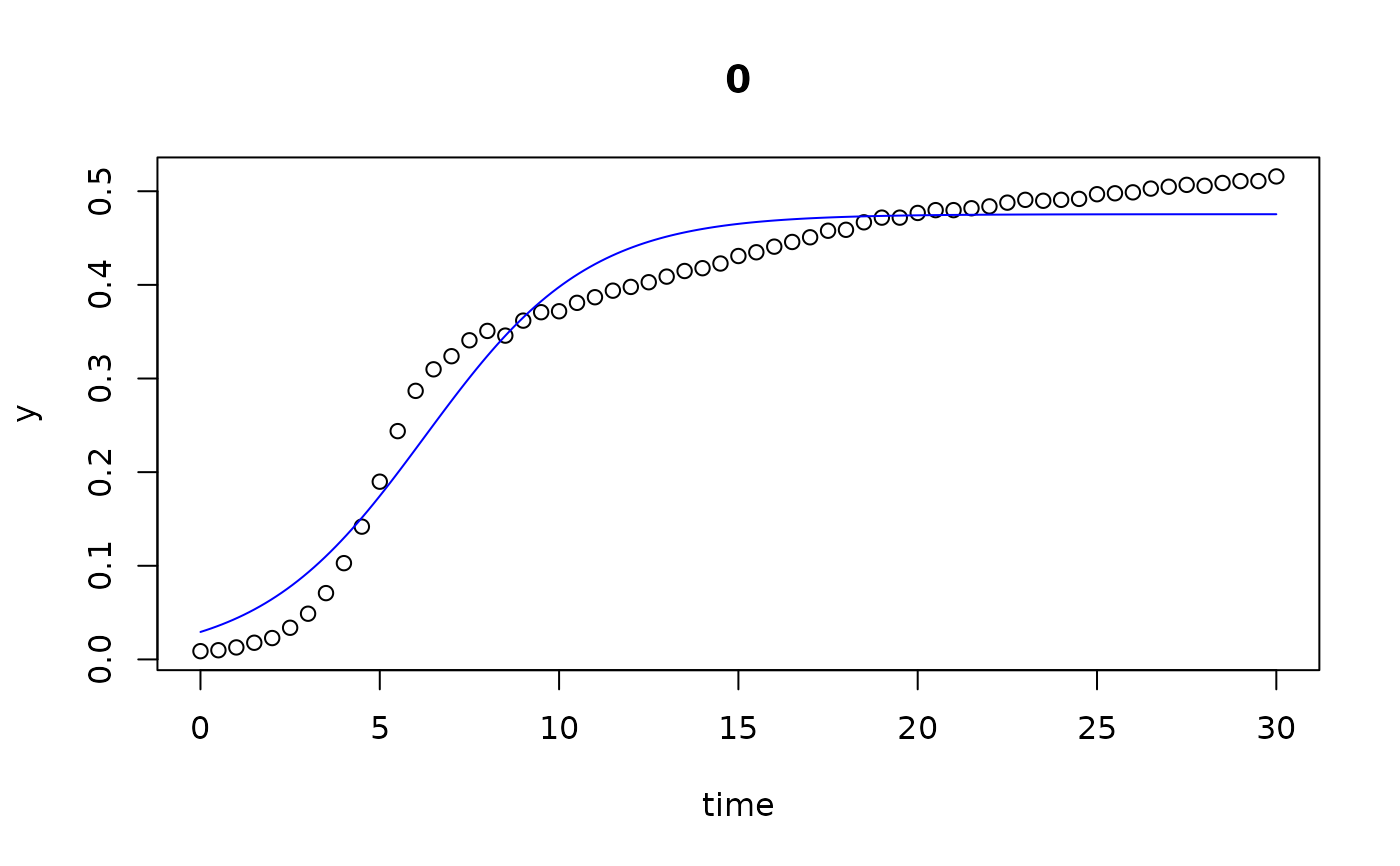
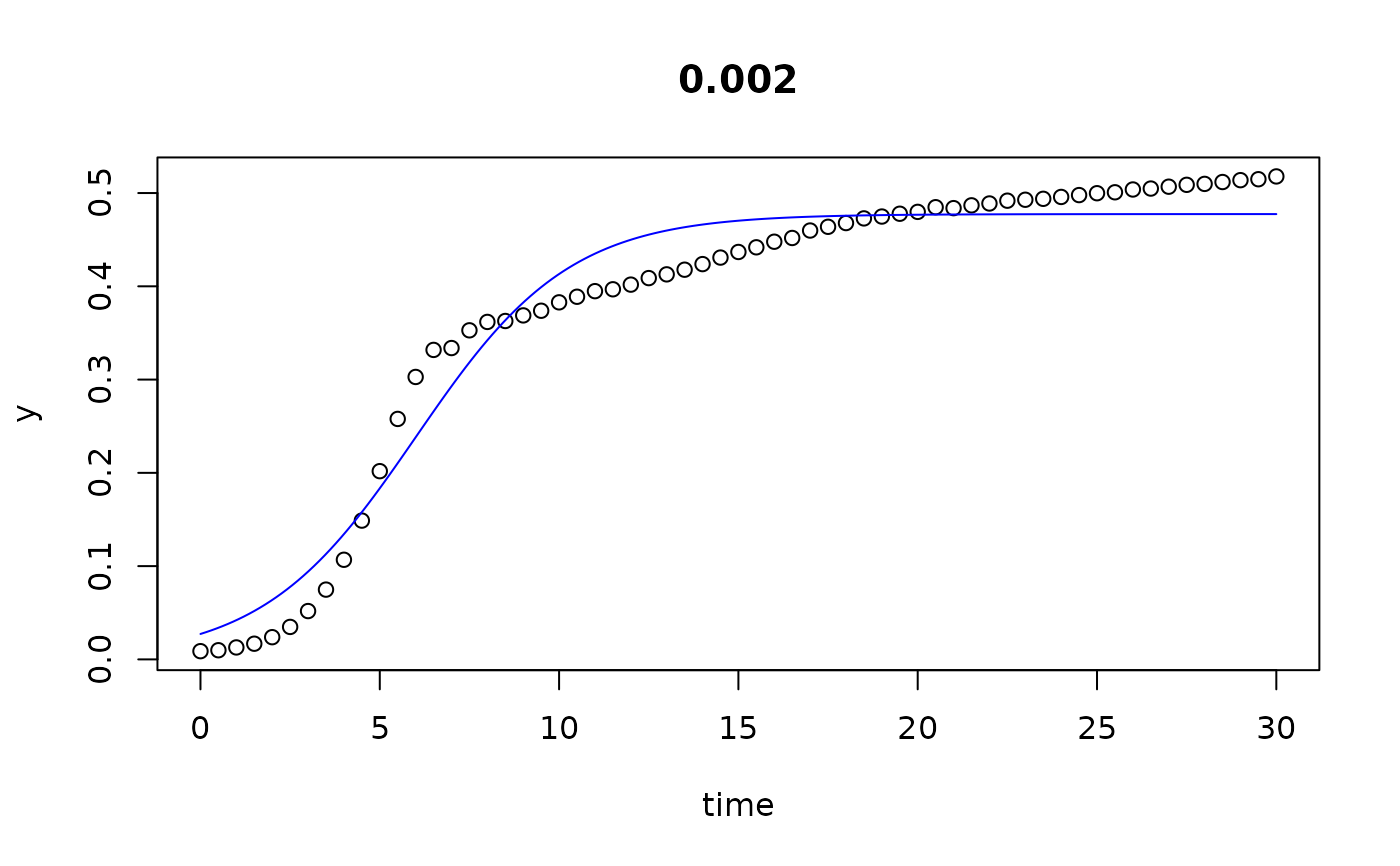
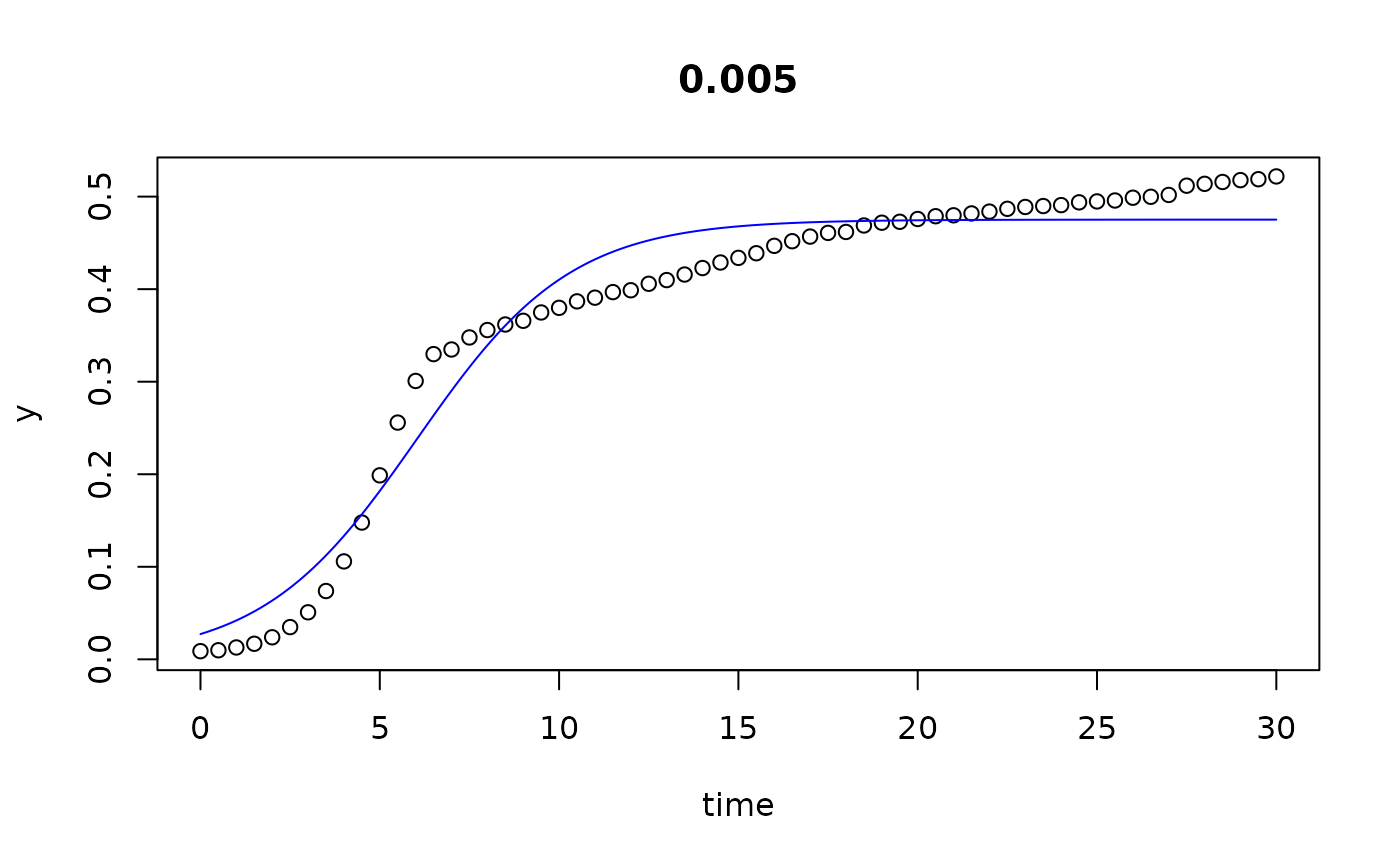
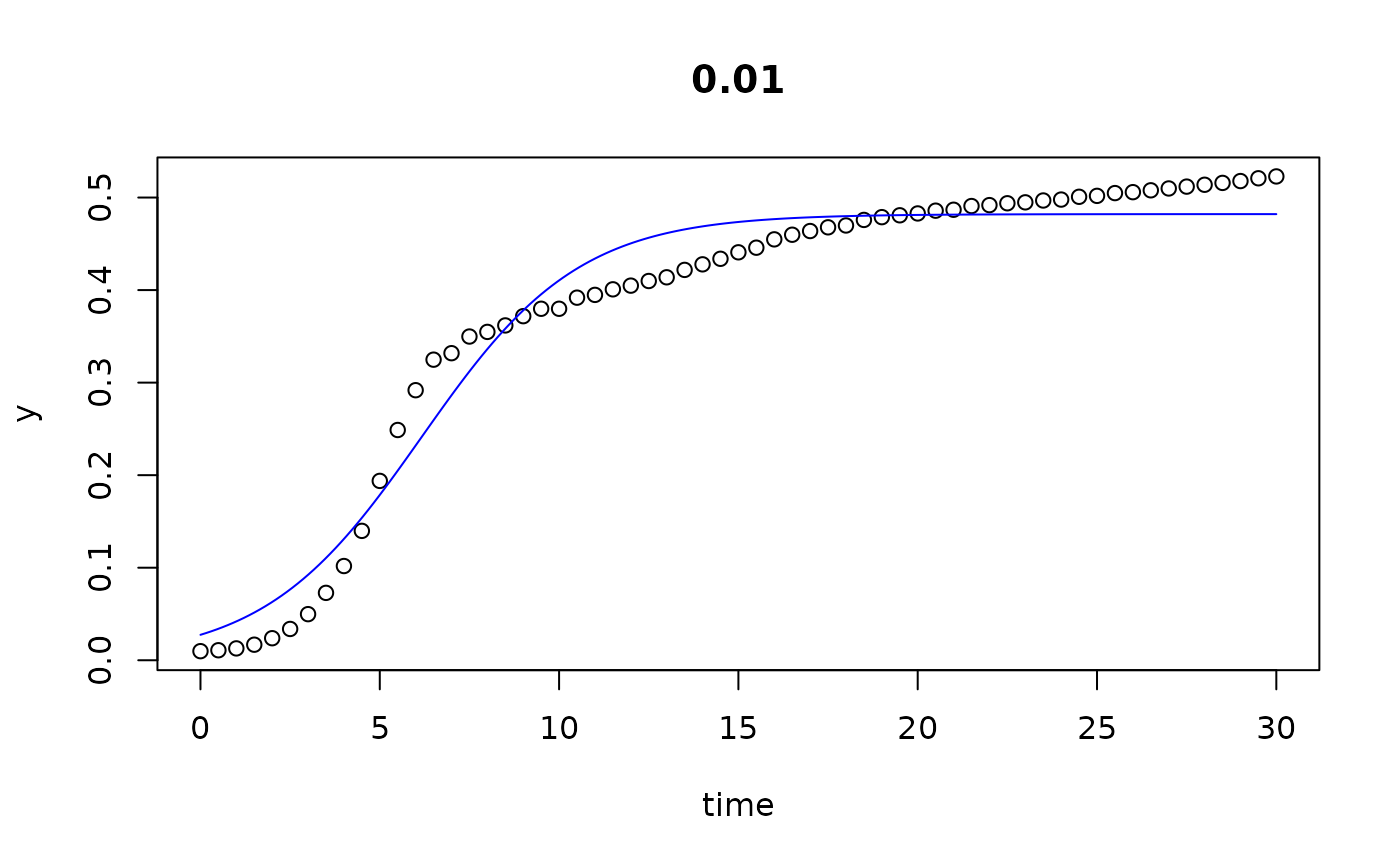
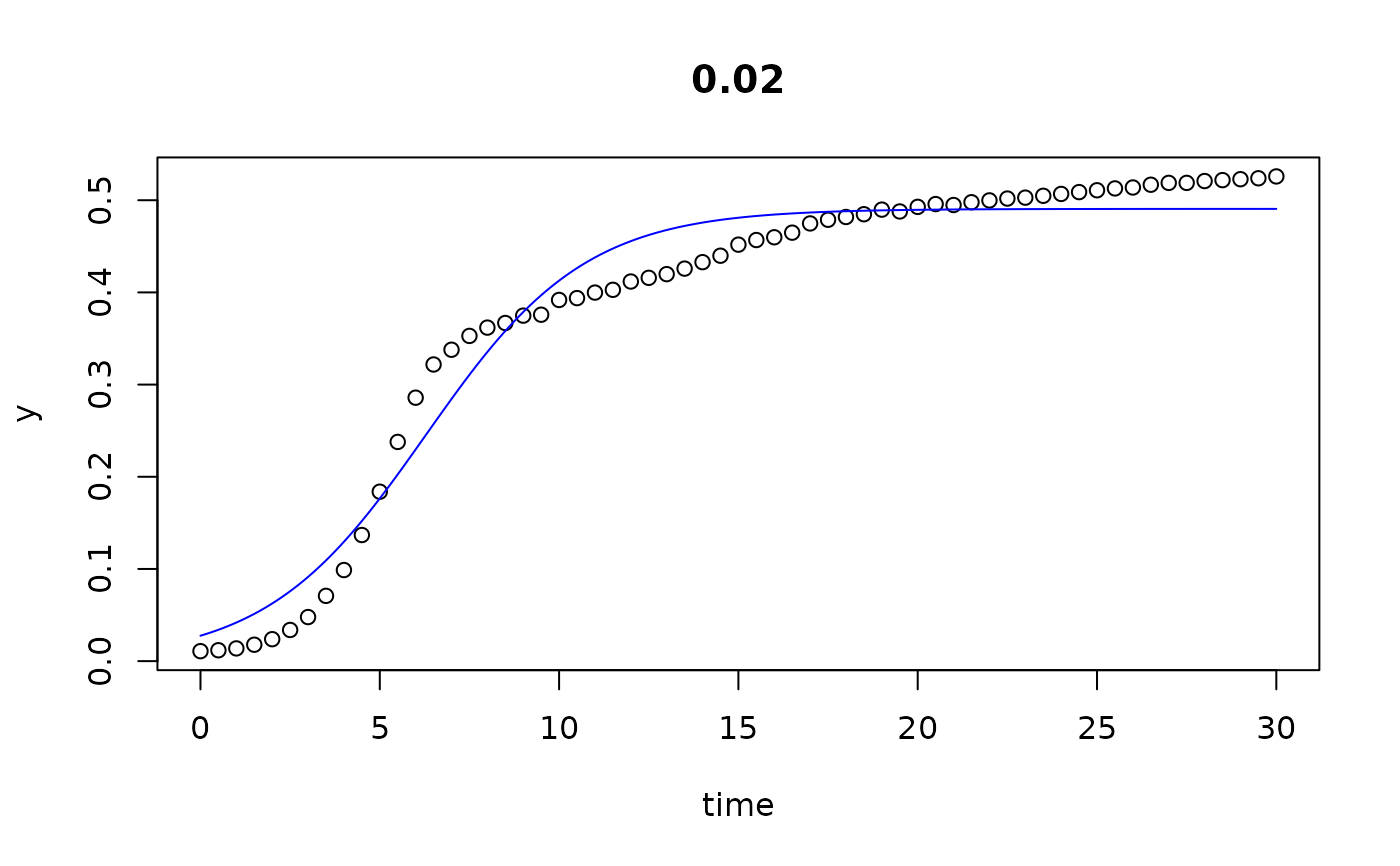
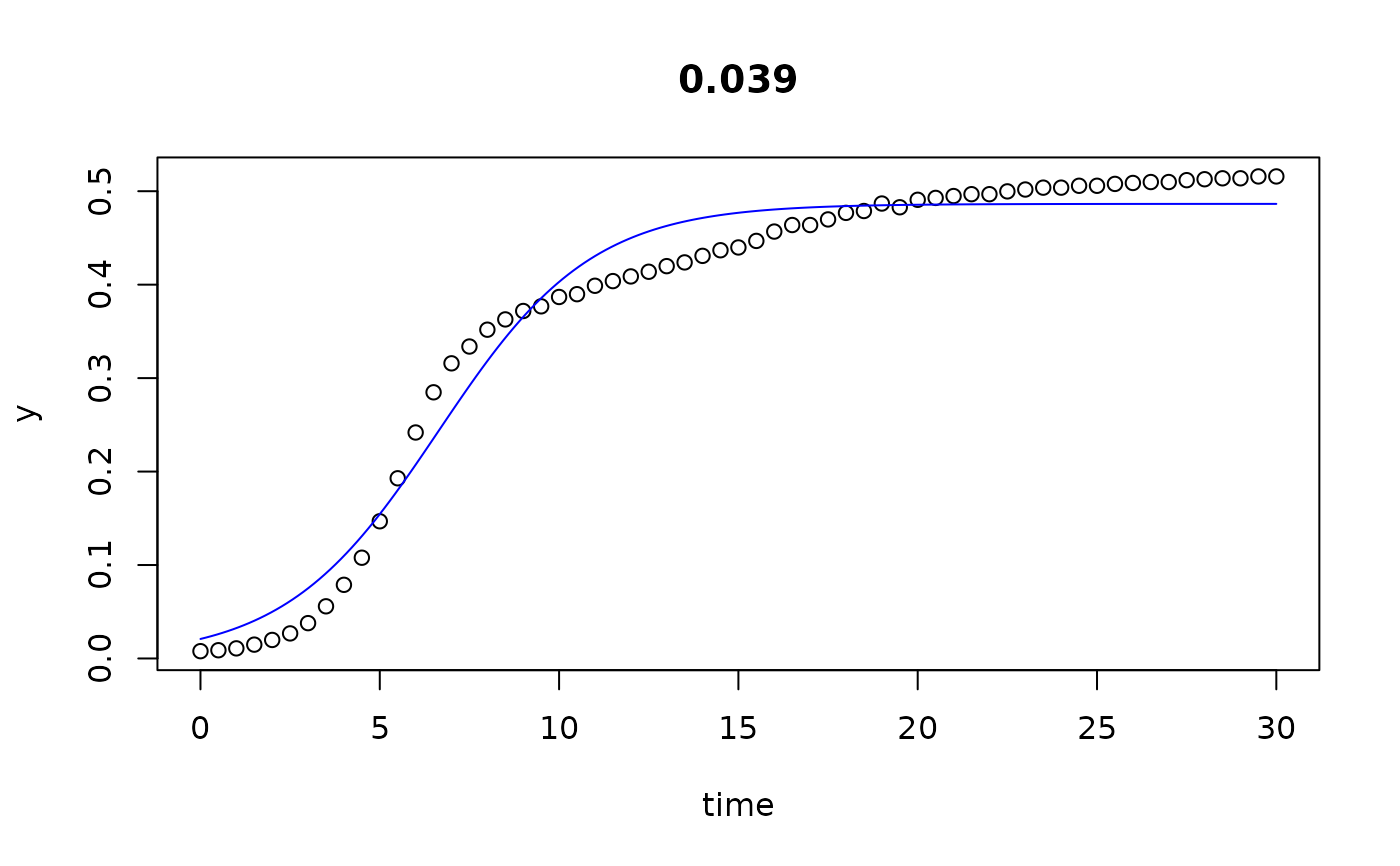
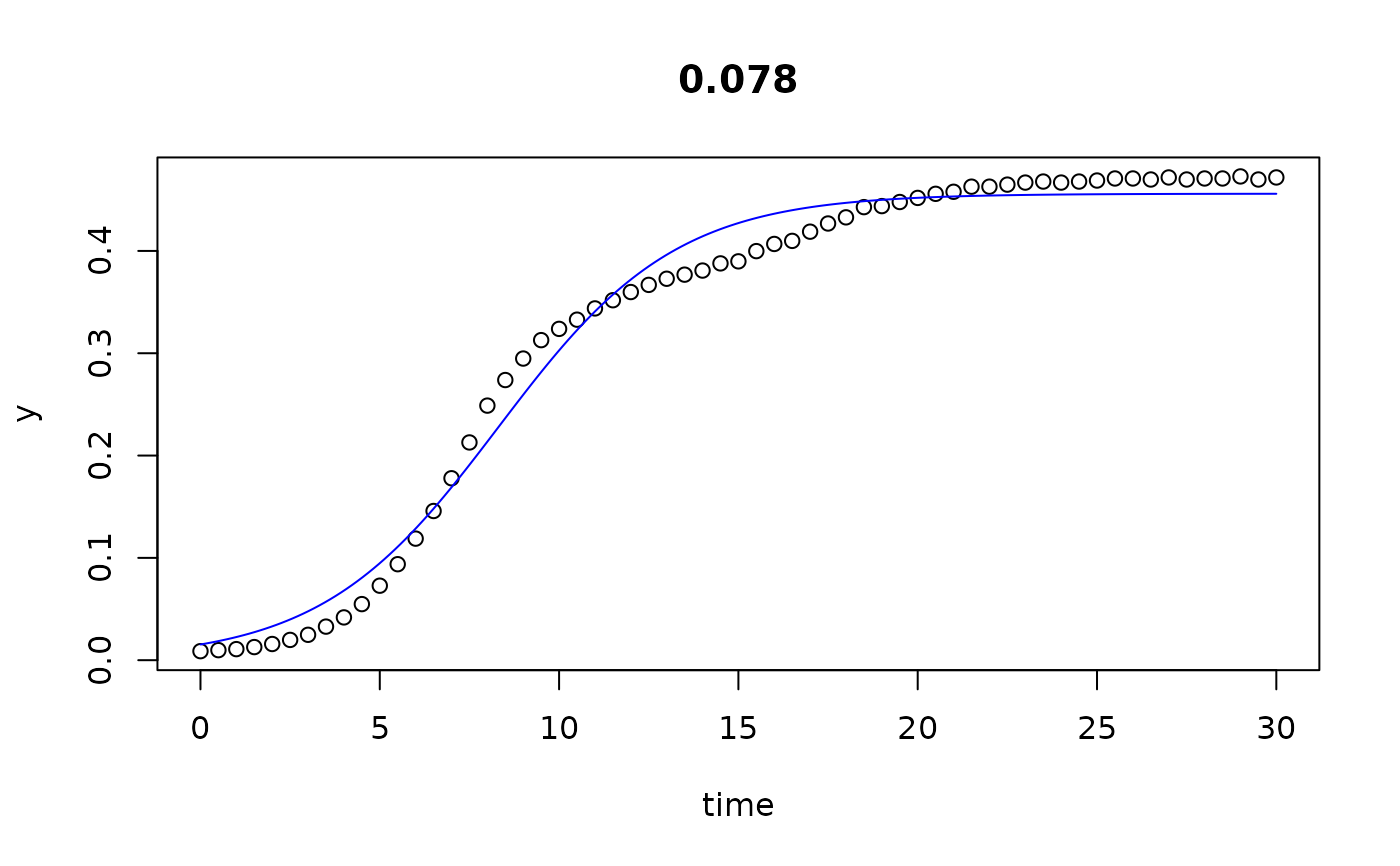
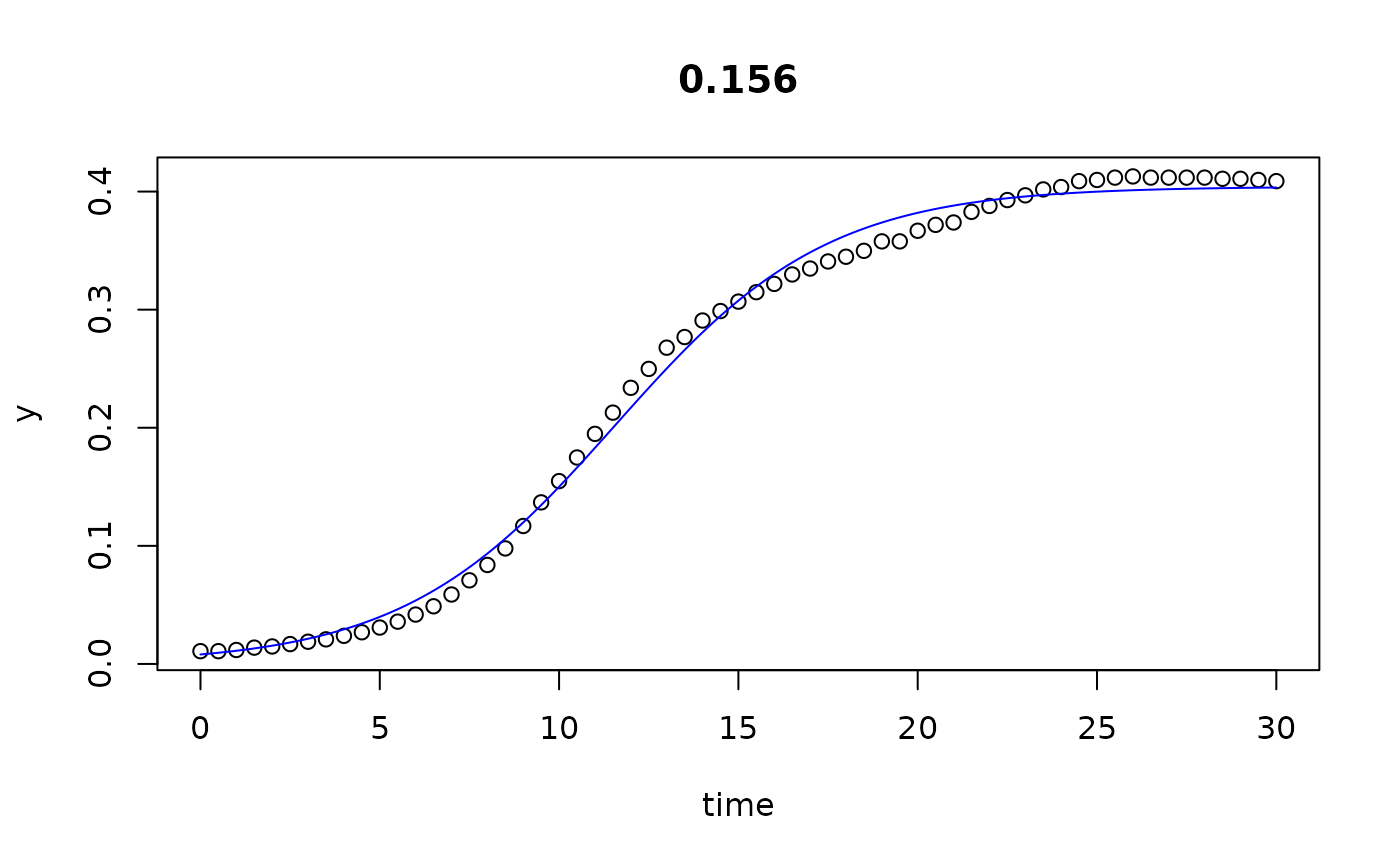
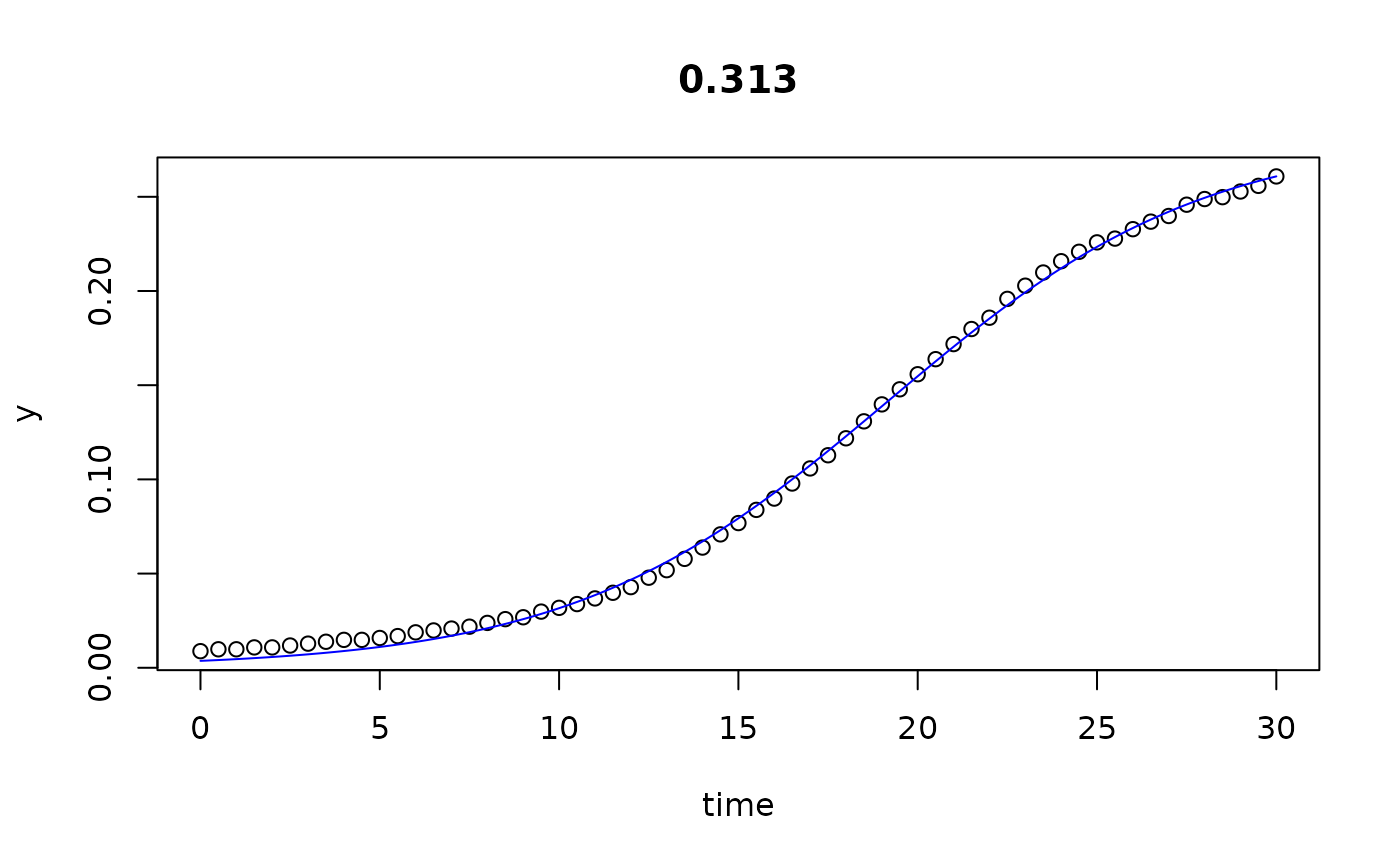
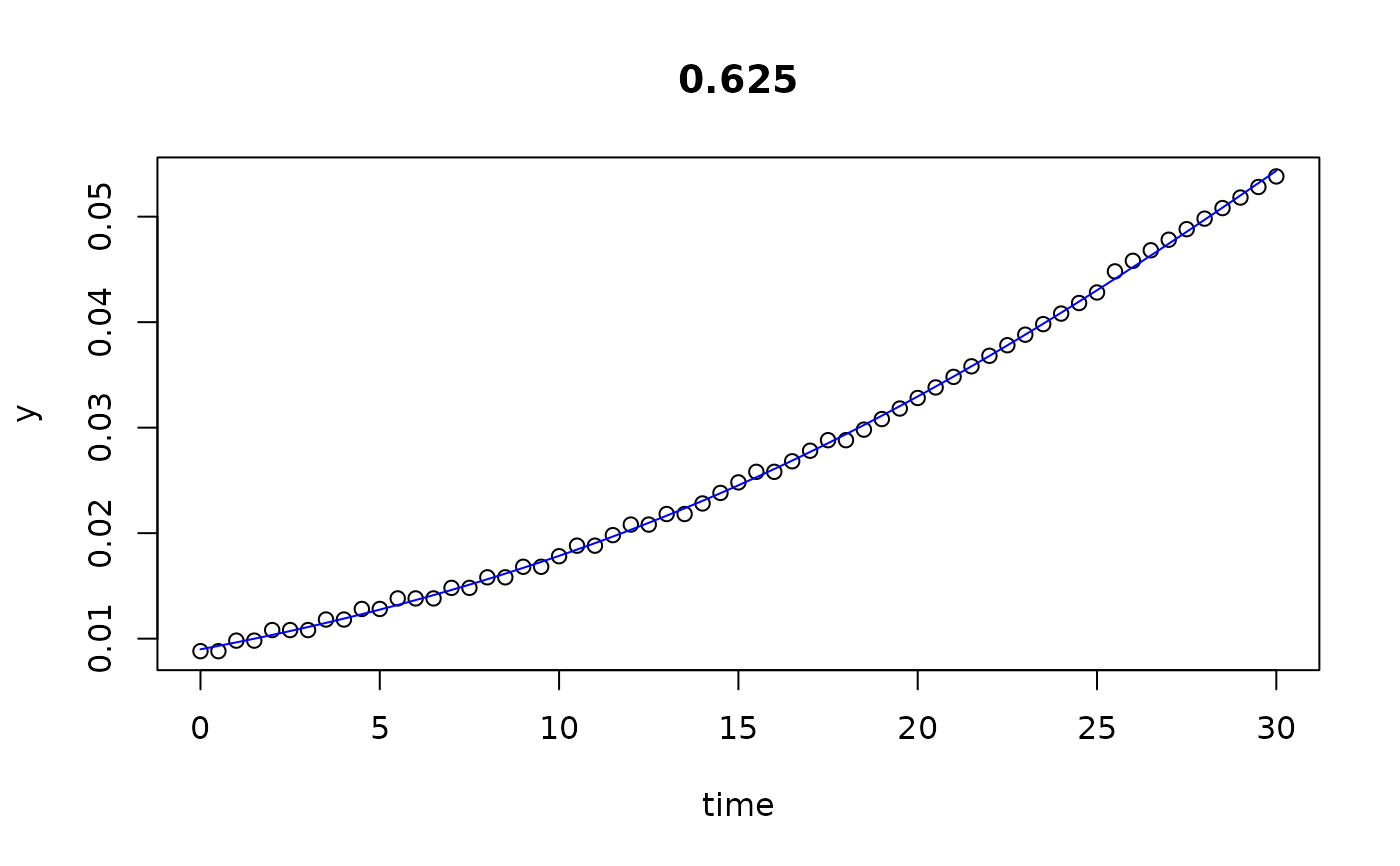
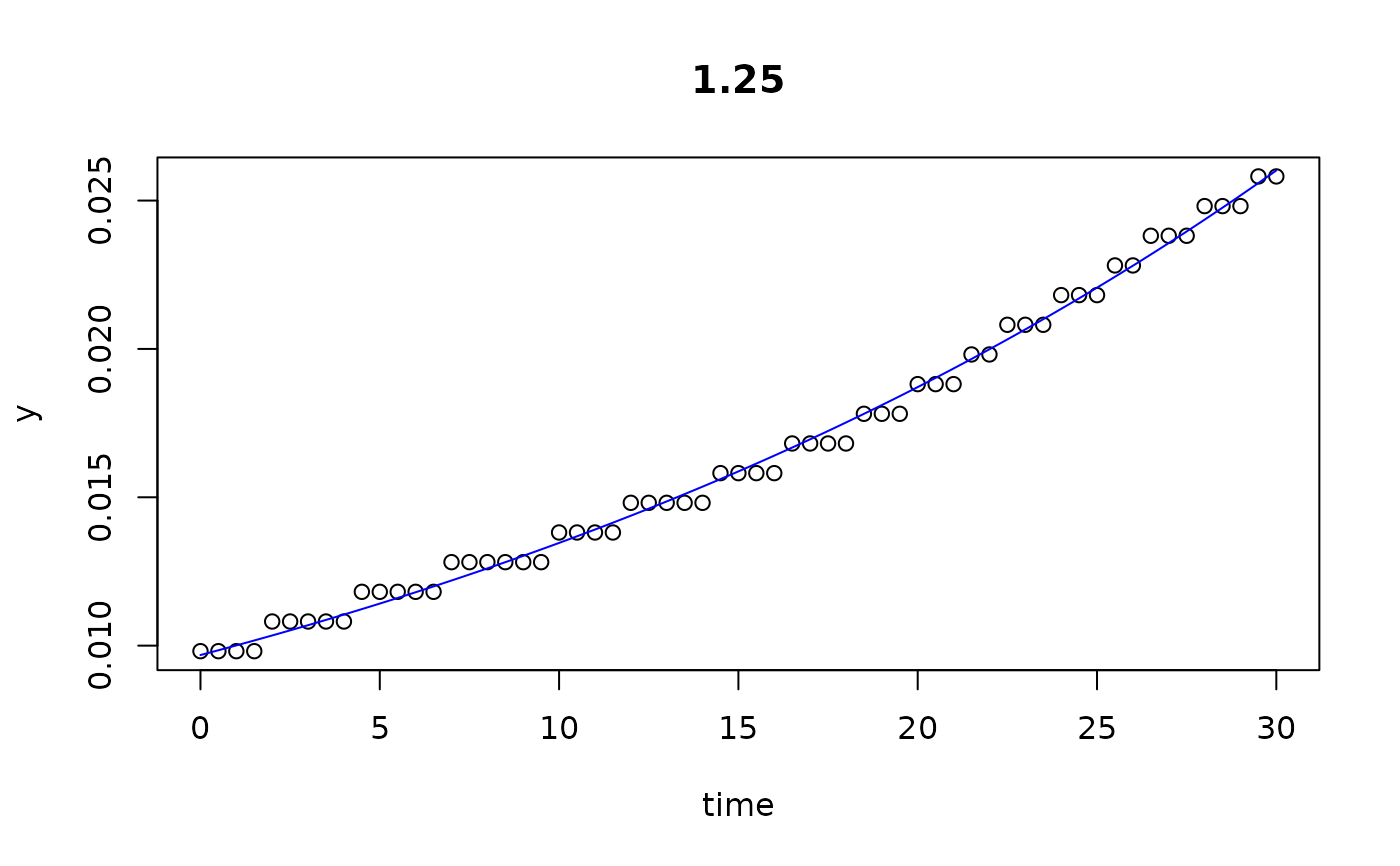
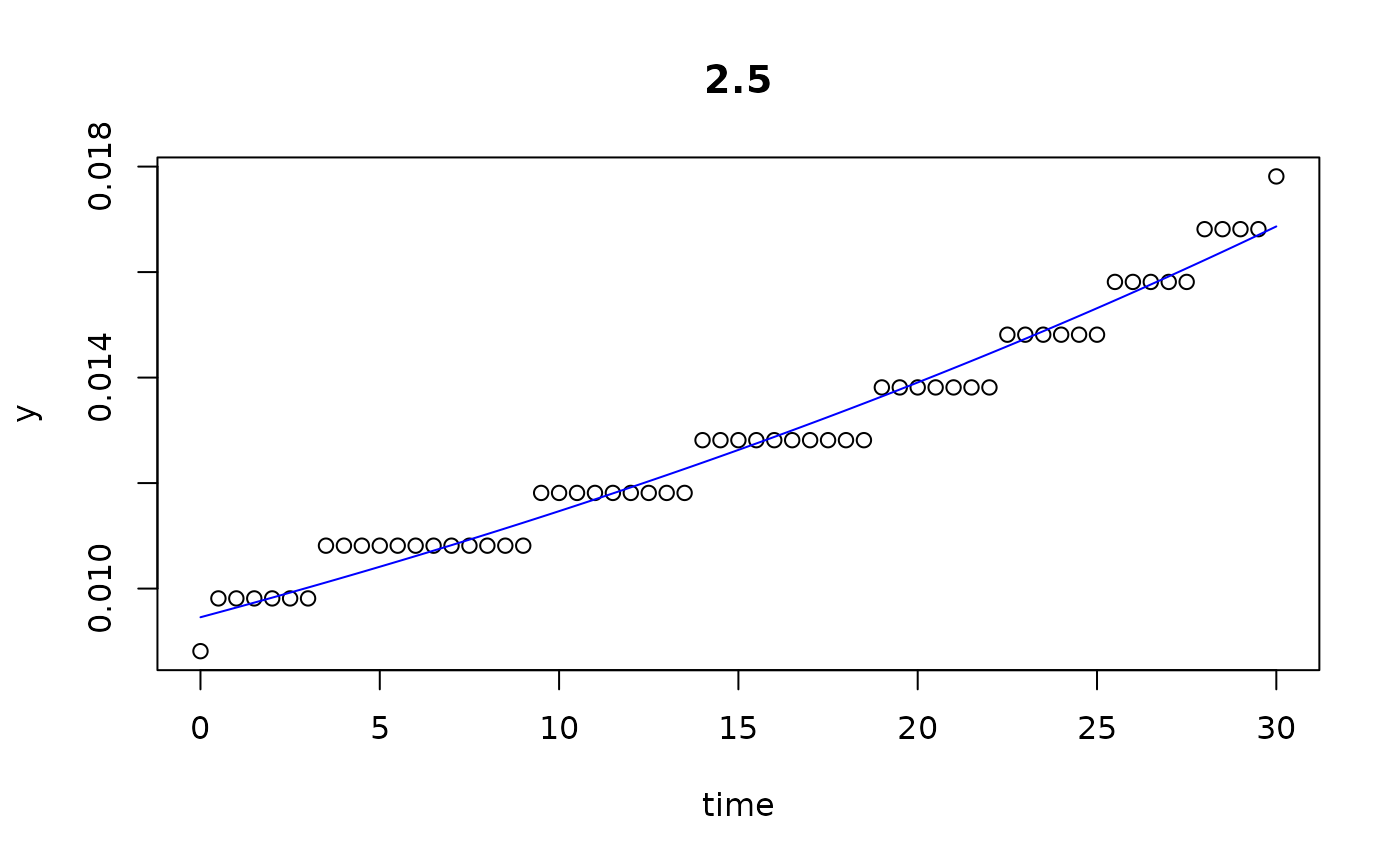results(all, extended=TRUE)
#>        conc          y0      mumax            K turnpoint         sat1
#> 0     0.000 0.029334991 0.43545804 4.754685e-01  6.250515 9.274825e+00
#> 0.002 0.002 0.027259902 0.46653469 4.774422e-01  6.010759 8.833627e+00
#> 0.005 0.005 0.027288802 0.46419629 4.751414e-01  6.027581 8.864648e+00
#> 0.01  0.010 0.027486632 0.45515405 4.820902e-01  6.164344 9.057787e+00
#> 0.02  0.020 0.027556609 0.44897724 4.906198e-01  6.284553 9.217798e+00
#> 0.039 0.039 0.020879178 0.46785804 4.864444e-01  6.635559 9.450427e+00
#> 0.078 0.078 0.015355180 0.40381858 4.559296e-01  8.312216 1.157348e+01
#> 0.156 0.156 0.008027564 0.33717987 4.042182e-01 11.563616 1.546940e+01
#> 0.313 0.313 0.003670851 0.22588498 2.835147e-01 19.185923 2.501613e+01
#> 0.625 0.625 0.008988866 0.07656636 1.247073e-01 29.999932 6.830539e-05
#> 1.25  1.250 0.009683618 0.03294199 2.761144e+05 29.999932 6.830539e-05
#> 2.5   2.500 0.009456558 0.01928594 1.171006e+05 29.999932 6.830539e-05
#>               sat2      sat3        r2
#> 0     1.084338e+01  13.01222 0.9637041
#> 0.002 1.029769e+01  12.32207 0.9615246
#> 0.005 1.033610e+01  12.37069 0.9604411
#> 0.01  1.055846e+01  12.63345 0.9647900
#> 0.02  1.073912e+01  12.84266 0.9671718
#> 0.039 1.091036e+01  12.92900 0.9745931
#> 0.078 1.326493e+01  15.60370 0.9862631
#> 0.156 1.749517e+01  20.29615 0.9956718
#> 0.313 2.803999e+01  32.22103 0.9987675
#> 0.625 5.655880e+01  71.82804 0.9994673
#> 1.25  1.610931e+08 610.47700 0.9952760
#> 2.5   1.800042e+08 999.49884 0.9737259
## we see that the the last 3 series (10...12) do not go into saturation
## within the observation time period.

## We can try to extend the search range:
results(all[10:12], extended=TRUE, time=c(0, 5000))
#>        conc          y0      mumax            K turnpoint      sat1      sat2
#> 0.625 0.625 0.008988866 0.07656636 1.247073e-01  33.37201  50.57221  59.49314
#> 1.25  1.250 0.009683618 0.03294199 2.761144e+05 521.09448 561.07255 581.80726
#> 2.5   2.500 0.009456558 0.01928594 1.171006e+05 846.82600 915.11192 950.52850
#>            sat3        r2
#> 0.625  71.82804 0.9994673
#> 1.25  610.47700 0.9952760
#> 2.5   999.49884 0.9737259


## =========================================================================
## visualisation how the 'extended parameters' are derived
## =========================================================================

# Derivatives of the logistic:
#   The 1st and 2nd derivatives are internal functions of the package.
#   They are used here for the visualisation of the algorithm.

deriv1 <- function(time, y0, mumax, K) {
  ret <- (K*mumax*y0*(K - y0)*exp(mumax * time))/
    ((K + y0 * (exp(mumax * time) - 1))^2)
  unname(ret)
}

deriv2 <- function(time, y0, mumax, K) {
  ret <- -(K * mumax^2 * y0 * (K - y0) * exp(mumax * time) *
             (-K + y0 * exp(mumax * time) + y0))/
    (K + y0 * (exp(mumax * time) - 1))^3
  unname(ret)
}
## =========================================================================

data(bactgrowth)
## extract one growth experiment by name
dat <- multisplit(bactgrowth, c("strain", "conc", "replicate"))[["D:0:1"]]


## unconstraied fitting
p <- c(y0 = 0.01, mumax = 0.2, K = 0.1) # start parameters
fit1 <- fit_growthmodel(FUN = grow_logistic, p = p, dat$time, dat$value)
summary(fit1)
#> 
#> Parameters:
#>       Estimate Std. Error t value Pr(>|t|)    
#> y0    0.017483   0.001581   11.06 9.98e-12 ***
#> mumax 0.200070   0.013979   14.31 2.10e-14 ***
#> K     0.099626   0.001850   53.87  < 2e-16 ***
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 
#> Residual standard error: 0.004246 on 28 degrees of freedom
#> 
#> Parameter correlation:
#>            y0   mumax       K
#> y0     1.0000 -0.8689  0.4537
#> mumax -0.8689  1.0000 -0.7048
#> K      0.4537 -0.7048  1.0000
p <- coef(fit1, extended=TRUE)

## copy parameters to separate variables to improve readability ------------
y0 <-    p["y0"]
mumax <- p["mumax"]
K  <-    p["K"]
turnpoint <- p["turnpoint"]
sat1 <-  p["sat1"]  # 2nd derivative
sat2 <-  p["sat2"]  # intercept between steepest increase and K
sat3 <-  p["sat3"]  # a given quantile of K, default 95\%

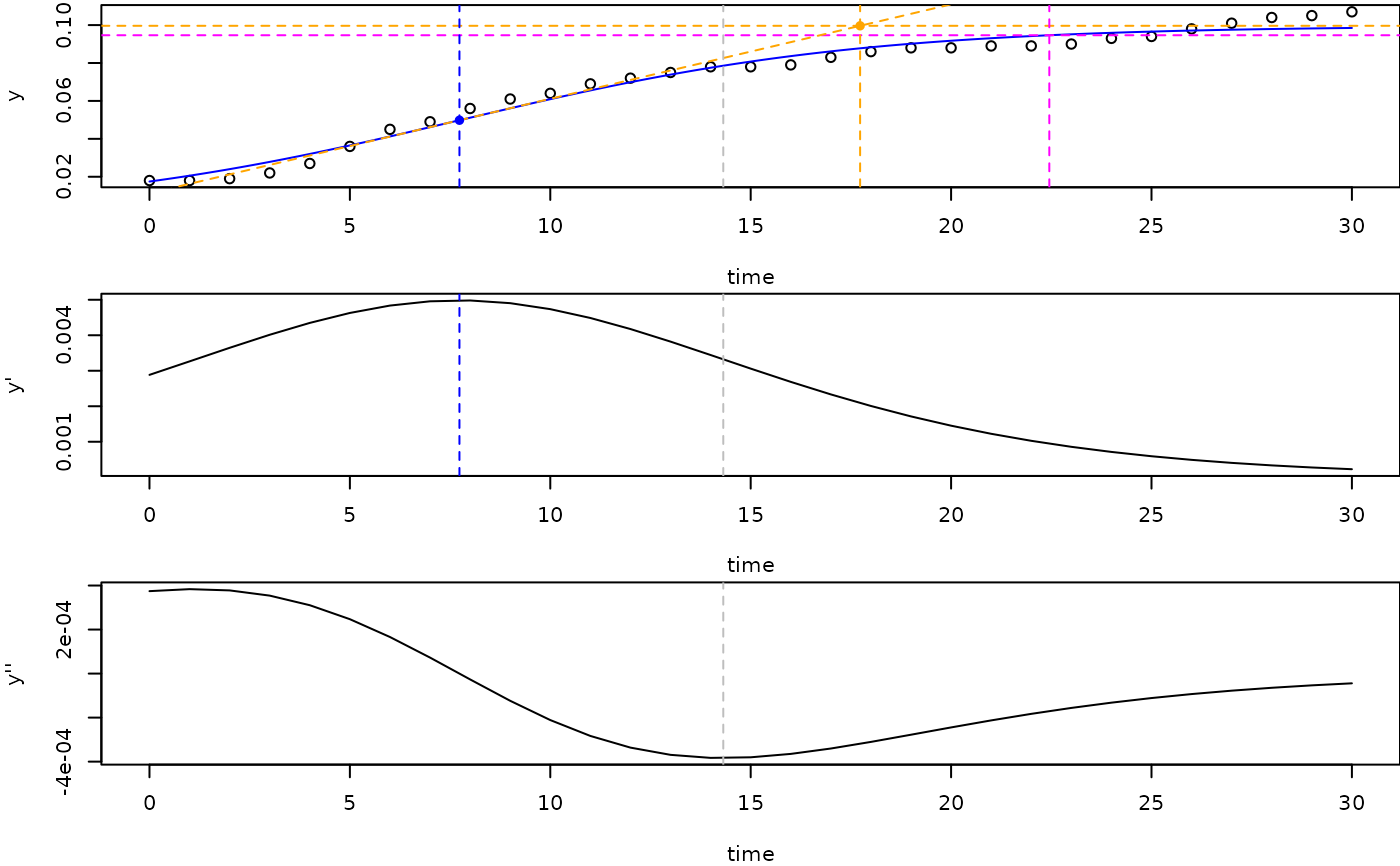
## show saturation values in growth curve and 1st and 2nd derivatives ------
opar <- par(no.readonly=TRUE)
par(mfrow=c(3, 1), mar=c(4,4,0.2,0))
plot(fit1)

## 95% saturation
abline(h=0.95*K, col="magenta", lty="dashed")

## Intercept between steepest increase and 100% saturation
b <- deriv1(turnpoint, y0, mumax, K)
a <- K/2 - b*turnpoint
abline(a=a, b=b, col="orange", lty="dashed")
abline(h=K, col="orange", lty="dashed")
points(sat2, K, pch=16, col="orange")
points(turnpoint, K/2, pch=16, col="blue")

## sat2 is the minimum of the 2nd derivative
abline(v=c(turnpoint, sat1, sat2, sat3),
       col=c("blue", "grey", "orange", "magenta"), lty="dashed")

## plot the derivatives
with(dat, plot(time, deriv1(time, y0, mumax, K), type="l", ylab="y'"))
abline(v=c(turnpoint, sat1), col=c("blue", "grey"), lty="dashed")

with(dat, plot(time, deriv2(time, y0, mumax, K), type="l",  ylab="y''"))
abline(v=sat1, col="grey", lty="dashed")

par(opar)