Skip to contents

Twostep Growth Model

Source: R/grow_twostep.R
grow_twostep.Rd

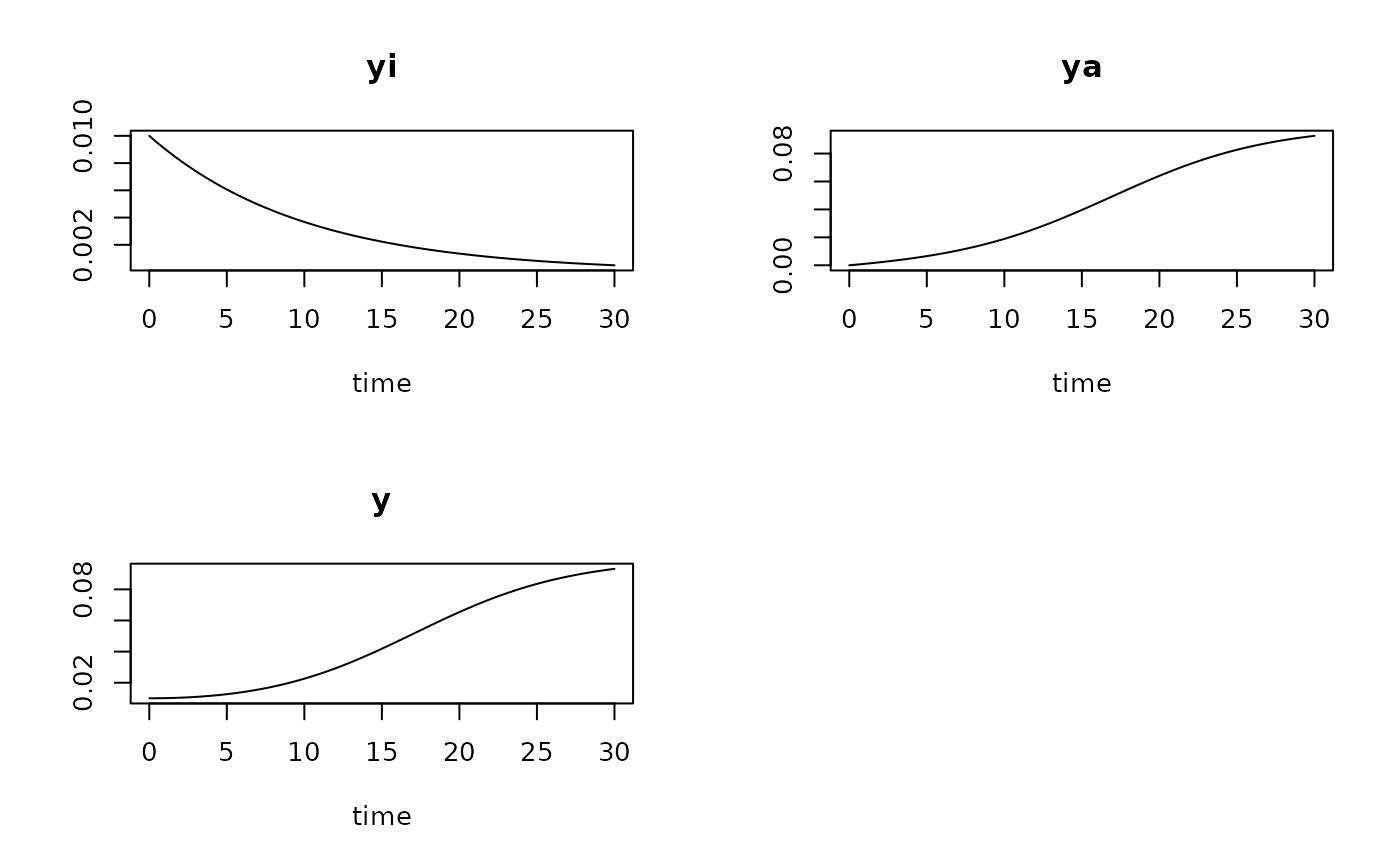
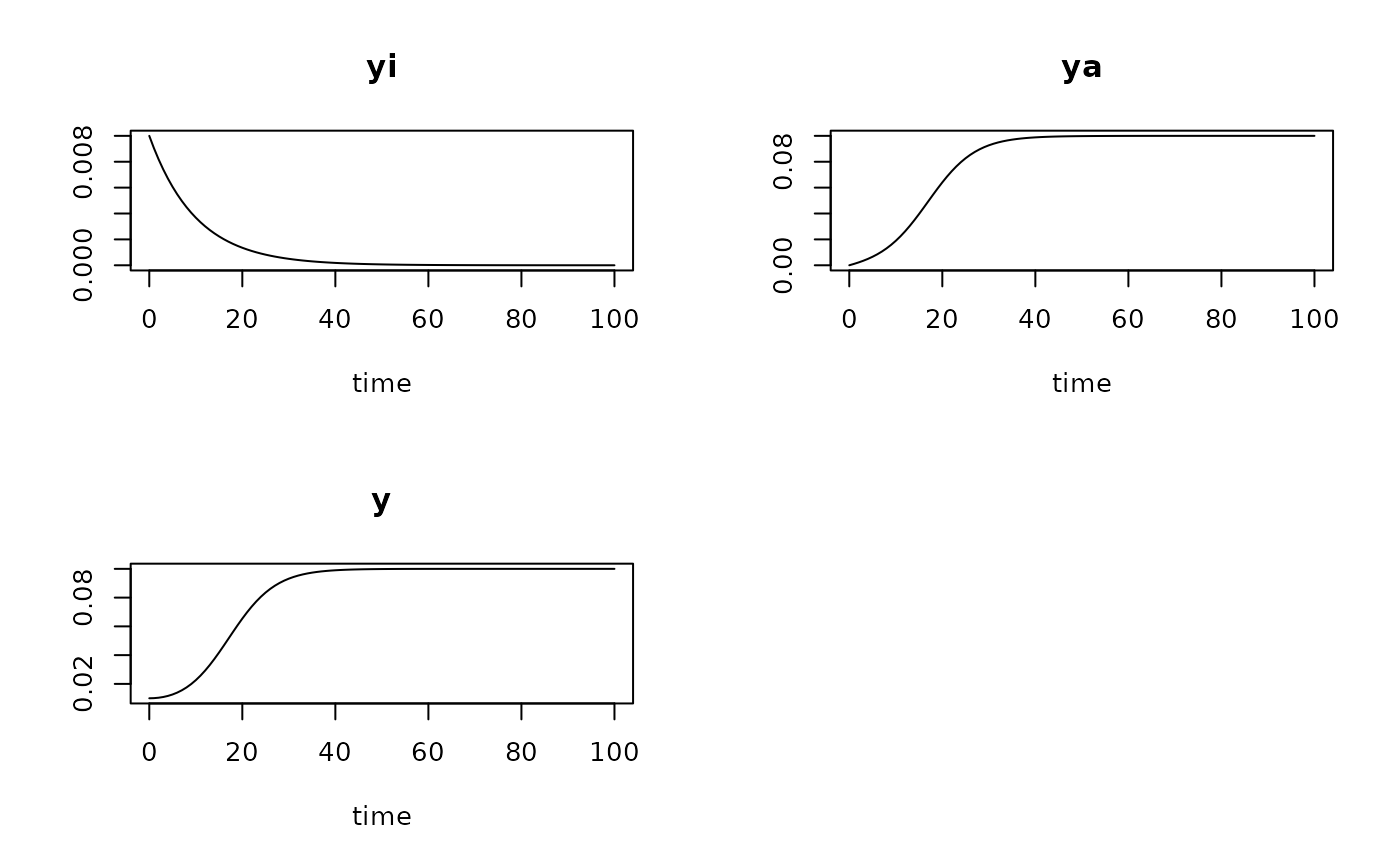
System of two differential equations describing bacterial growth as two-step process of activation (or adaptation) and growth.

Usage

ode_twostep(time, y, parms, ...)

grow_twostep(time, parms, ...)

Arguments

time

actual time (for the ode) resp. vector of simulation time steps.

y

named vector with state of the system (yi, ya: abundance of inactive and active organisms, e.g. concentration of inactive resp. active cells).

parms

parameters of the two-step growth model:

  • yi, ya initial abundance of active and inactive organisms,

  • kw activation (“wakeup”) constant (1/time),

  • mumax maximum growth rate (1/time),

  • K carrying capacity (max. abundance).

...

placeholder for additional parameters (for user-extended versions of this function)

Value

For ode_twostep: matrix containing the simulation outputs. The return value of has also class deSolve.

For grow_twostep: vector of dependent variable (y):

  • time time of the simulation

  • yi concentration of inactive cells

  • ya concentration of active cells

  • y total cell concentration

Details

The model is given as a system of two differential equations:

$$dy_i/dt = -kw * yi$$ $$dy_a/dt = kw * yi + mumax * (1 - (yi + ya)/K) * ya$$

that are then numerically integrated ('simulated') according to time (t). The model assumes that the population consists of active (\(y_a\)) and inactive (\(y_i\)) cells so that the observed abundance is (\(y = y_i + y_a\)). Adapting inactive cells change to the active state with a first order 'wakeup' rate (\(kw\)).

Function ode_twostep is the system of differential equations, whereas grow_twostep runs a numerical simulation over time.

A similar two-compartment model, but without the logistic term, was discussed by Baranyi (1998).

References

Baranyi, J. (1998). Comparison of stochastic and deterministic concepts of bacterial lag. J. heor. Biol. 192, 403–408.

See also

Other growth models: grow_baranyi(), grow_exponential(), grow_gompertz(), grow_gompertz2(), grow_huang(), grow_logistic(), grow_richards(), growthmodel, ode_genlogistic()

Other growth models: grow_baranyi(), grow_exponential(), grow_gompertz(), grow_gompertz2(), grow_huang(), grow_logistic(), grow_richards(), growthmodel, ode_genlogistic()

Examples


time <- seq(0, 30, length=200)
parms <- c(kw = 0.1,  mumax=0.2, K=0.1)
y0    <-  c(yi=0.01, ya=0.0)
out   <- ode(y0, time, ode_twostep, parms)

plot(out)

o <- grow_twostep(0:100, c(yi=0.01, ya=0.0, kw = 0.1,  mumax=0.2, K=0.1))
plot(o)