Skip to contents

Growth Model According to Gompertz

Source: R/grow_gompertz2.R
grow_gompertz2.Rd

Gompertz growth model written as analytical solution of the differential equation system.

Usage

grow_gompertz2(time, parms)

grow_gompertz3(time, parms)

Arguments

time

vector of time steps (independent variable).

parms

named parameter vector of the Gompertz growth model with:

  • y0 initial value of abundance,

  • mumax maximum growth rate (1/time),

  • K maximum abundance (carrying capacity),

  • lambda time of lag phase of the 3 parameter Gompertz model .

Value

vector of dependent variable (y)

Details

The equation used here is:

$$y = y0*(K/y0)^(exp(-exp((exp(1)*mumax*(lambda - time))/log(K/y0)+1)))$$

Functions grow_gompert2 and grow_gompertz3 describe sigmoidal growth with an exponentially decreasing intrinsic growth rate with or without an additional lag parameter. The formula follows the reparametrization of Zwietering et al (1990), with parameters that have a biological meaning.

References

Tsoularis, A. (2001) Analysis of Logistic Growth Models. Res. Lett. Inf. Math. Sci, (2001) 2, 23-46.

Zwietering, M. H., Jongenburger, I., Rombouts, F. M., and Van't Riet, K. (1990). Modeling of the bacterial growth curve. Appl. Environ. Microbiol., 56(6), 1875-1881.

See also

Other growth models: grow_baranyi(), grow_exponential(), grow_gompertz(), grow_huang(), grow_logistic(), grow_richards(), growthmodel, ode_genlogistic(), ode_twostep()

Examples


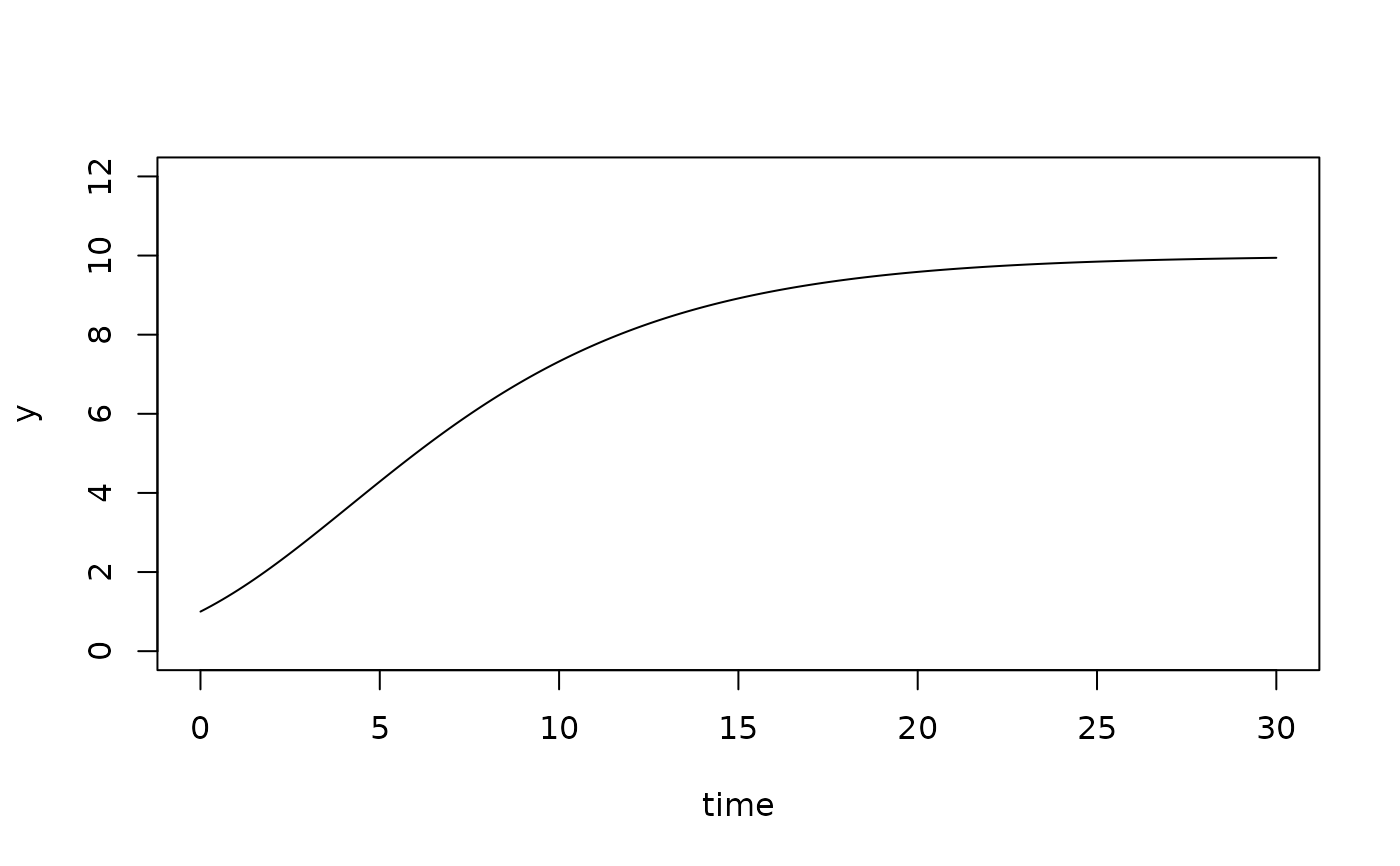
time <- seq(0, 30, length=200)
y    <- grow_gompertz(time, c(y0=1, mumax=.2, K=10))[,"y"]
plot(time, y, type="l", ylim=c(0, 12))