library(Kendall)
data(PrecipGL)
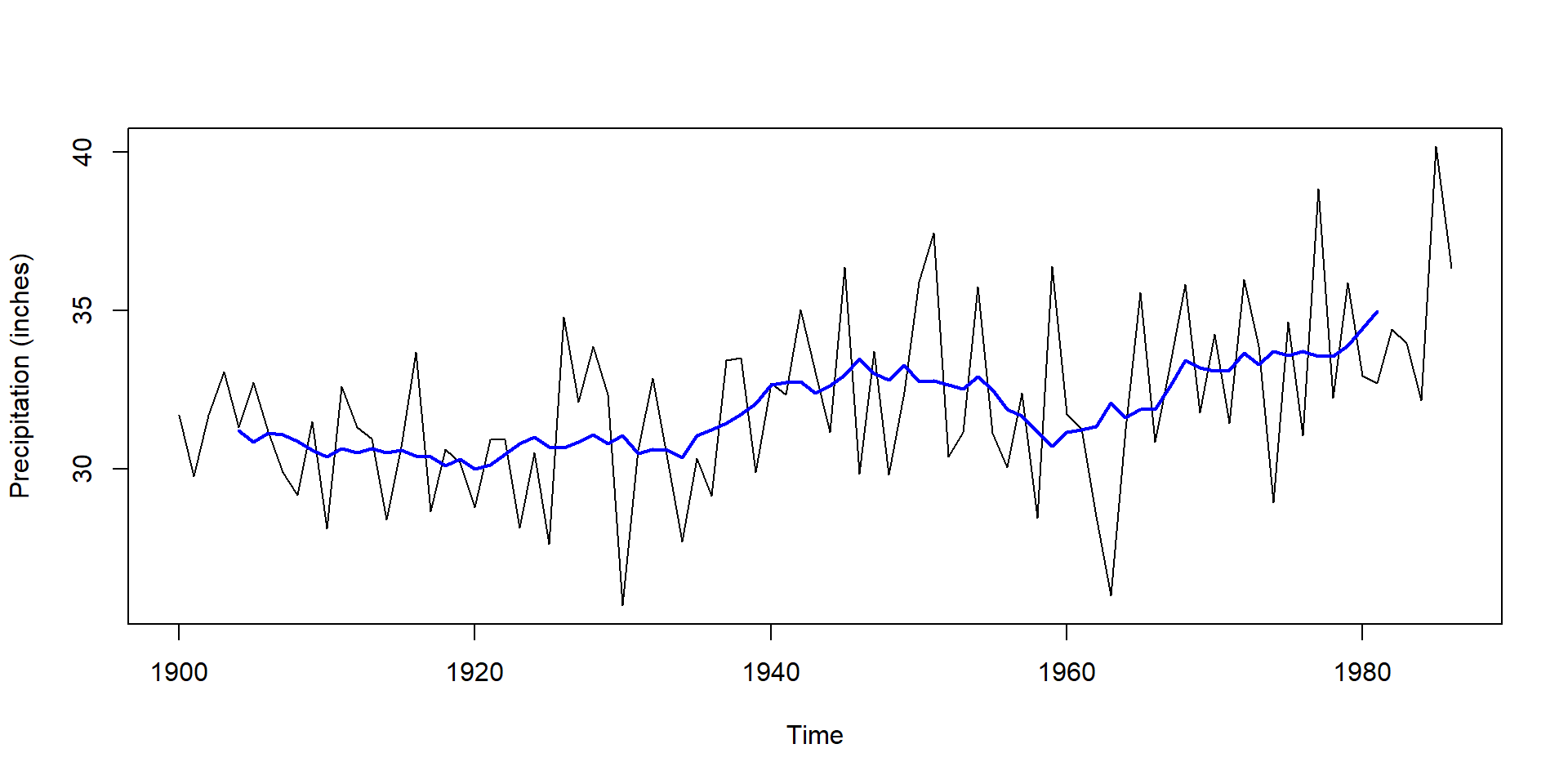
plot(PrecipGL, ylab="Precipitation (inches)")
# moving average with rectangular kernel
kernel <- rep(1, 10) # change second value to play with bandwidth
lines(stats::filter(PrecipGL, kernel/sum(kernel)), lwd = 2, col = "blue")10-Time Series Outlook
Applied Statistics – A Practical Course
2026-01-13
Time series decomposition
Time series decomposition
Traditional component model
Decomposition of time series into:
- trend component,
- seasonal or periodic component and
- stochastic component.
Assumptions
- additivity of components
- approximate normal distribution of residuals
- homogeneous variance (of residuals)
If distribution is skewed, effects are “multiplicative”, or variance changes proportionally with trend \(\rightarrow\), consider transformation.
For hydrological or biomass data with right-skewed distribution, log-transformation can be helpful.
Smoothing methods
- alternative to parametric linear or non-linear regression vs. time
- smoothers are based on moving averages
Example: Annual precipitation 1900-1986, Great Lakes
Trend corrected series
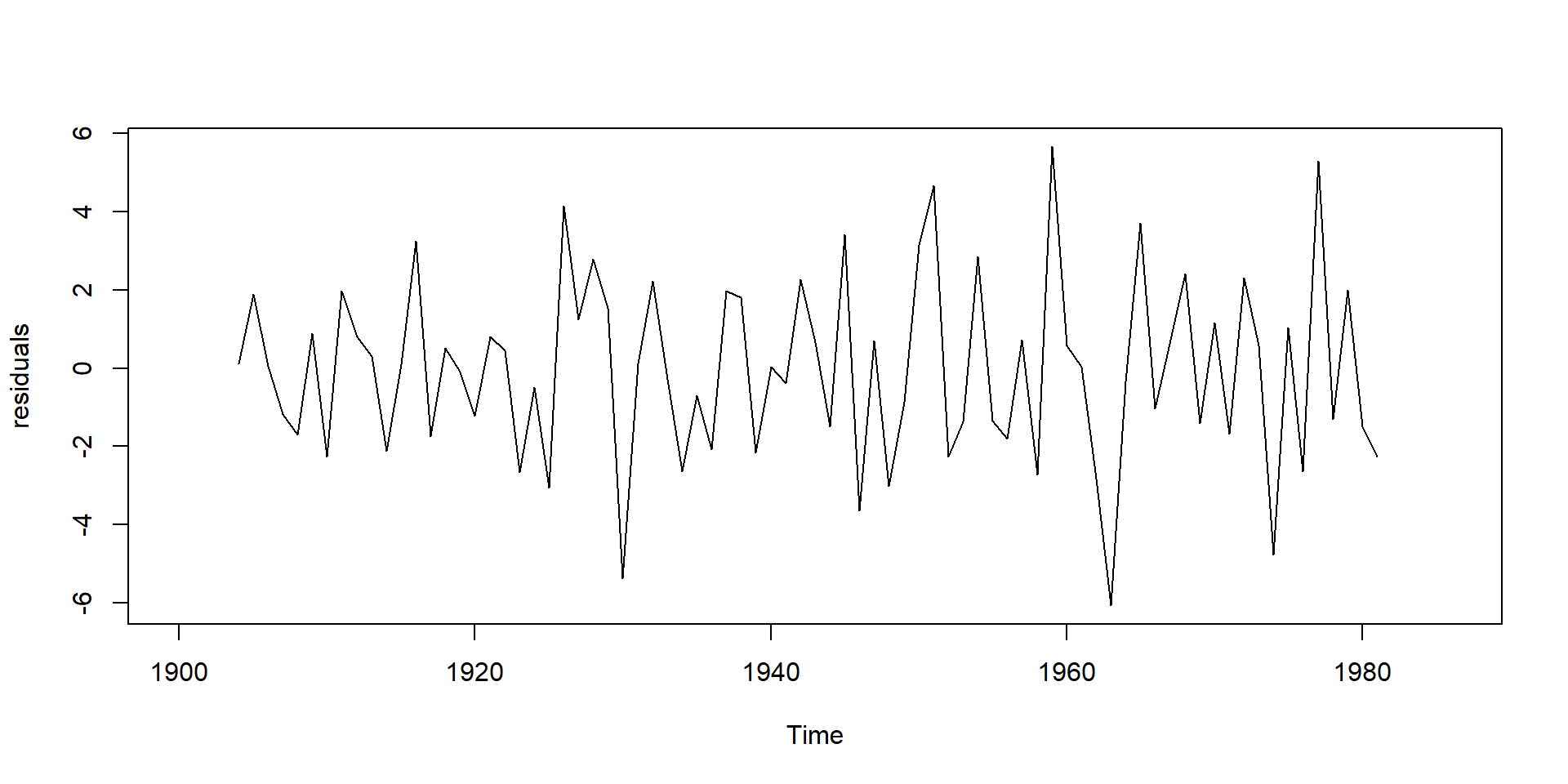
- Trend corrected series can be obtained by subtracting the trend.
- Note: use
stats::filterto avoid potential conflict withdplyr::filter.
Smoothing of data with 12monthly seasonality
- For a seasonal time series with monthly values Kleiber & Zeileis (2008) recommend a filter with 13 coefficients.
- Example: water level of Rio Negro 18 km upstream from its confluence with the Amazon River.
- The data set is contained in the package boot (Canty & Ripley, 2022):
[1] 1903.000 1992.917 12.000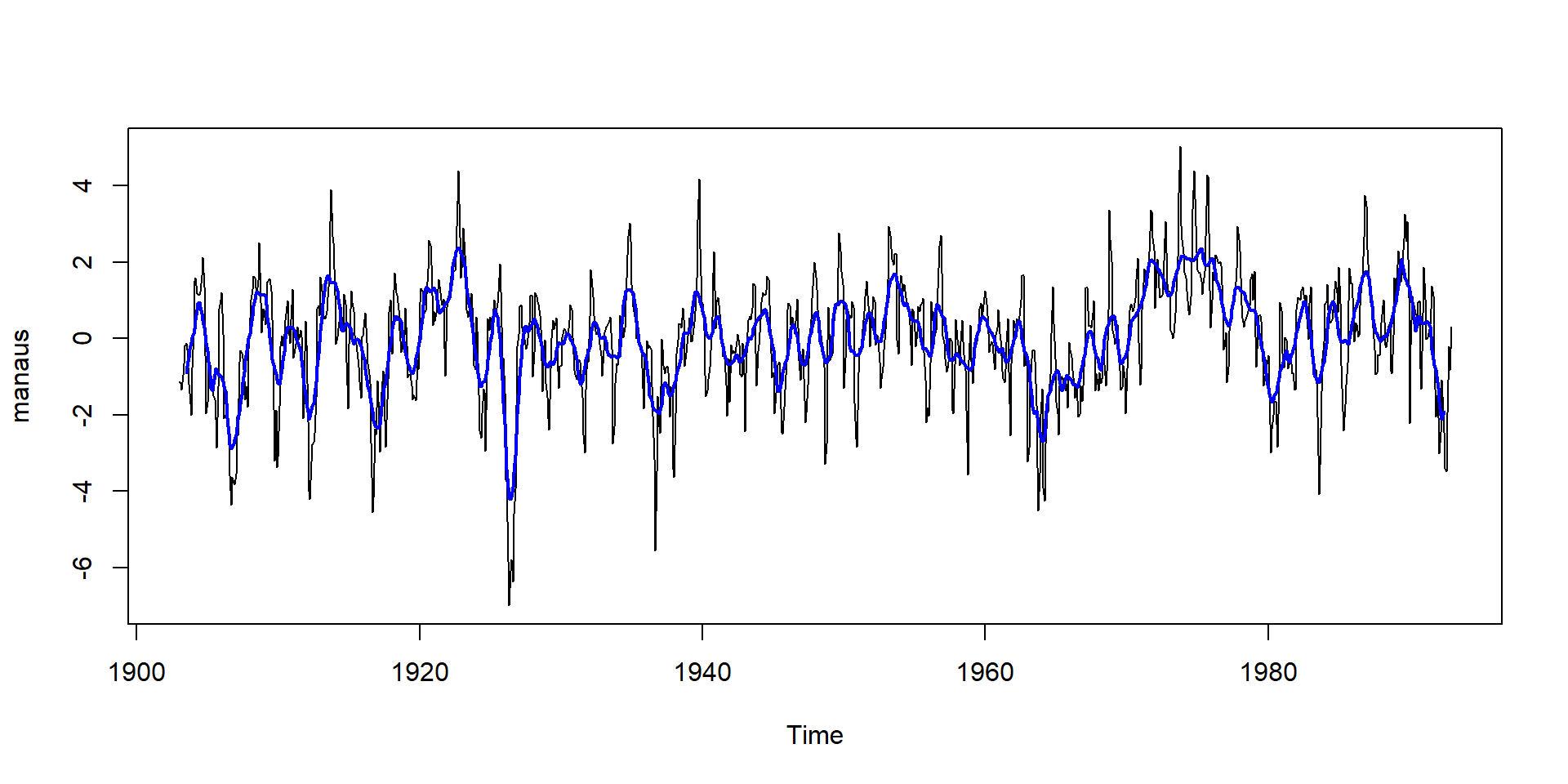
Very popular method: The LOWESS filter
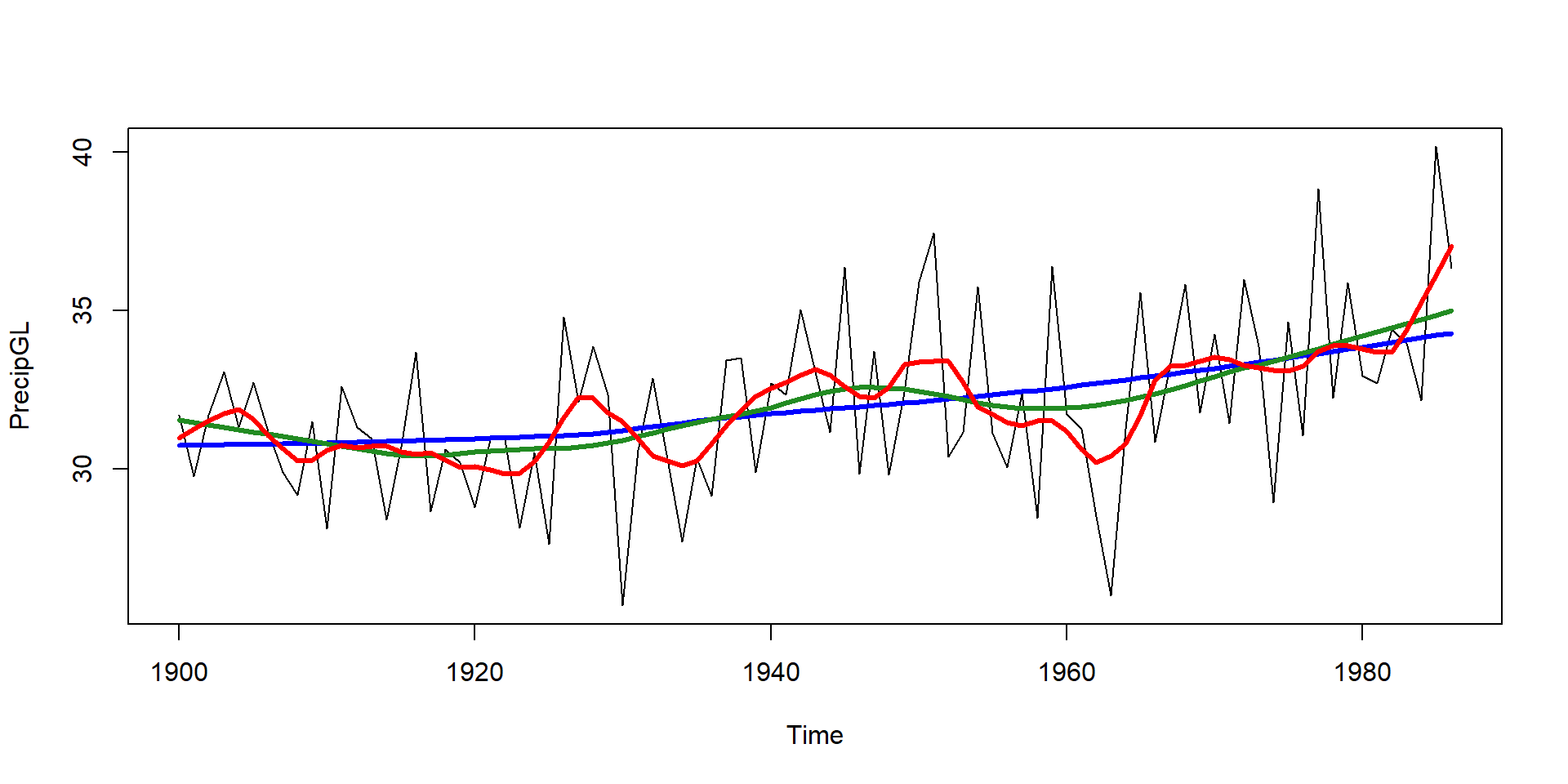
- locally weighted polynomial regression (W. S. Cleveland, 1979)
- allows to adjust smoothness (smoother span
f) - different functions available in R:
lowessandloess
Identification of seasonal components
Periodic phenomena are common in nature
- seasonal course of solar radiation and temperature
- seasonal development of vegetation
- heartbeat of animals.
Harmonic analysis
- every time series can be described as a sum of sine and a cosine functions with different periods (Fourier series)
\[ x_t = a_0 + \sum_{p=1}^{N/2-1} \big(a_p \cos(2 \pi p t/N) + b_p \sin(2 \pi p t/N)\big) +a_{N/2} \cos(\pi t), \qquad t=1 \dots N \]
with
\(x_t\): equidistant time series, \(t\): time step, \(N\): number of data, \(a_p, b_p\): Fourier coefficients,
\(a_0 = \bar{x}\), \(p\): order of the periodic component
Formulation with single cosine term and shift \(\Phi\)
- equation with sine and cosine terms can be transformed in an equation with cosine terms only
- use of trigonometric addition formulas:
\[ x_t = a_0 + \sum(R_p \cdot \cos(2 \pi p t / N + \Phi_p) \]
with:
- amplitude: \(R_p = \sqrt{a_p^2 + b_p^2}\)
- phase shift: \(\Phi_p = \arctan(-b_p/a_p)\)
see: https://en.wikipedia.org/wiki/List_of_trigonometric_identities
Different methods to identify seasonal parameters
- linear regression with the
lmfunction, e.g. for a single periodic component:
m <- lm(x ~ sin(2 * pi * t / N) + cos(2 * pi * t / N)) - nonlinear regression with
nls(allows to identify the period as nonlinear parameter) - classical Fourier analysis:
\[\begin{align} a_0 &= \bar{x}\\ a_{N/2} &= \sum_{t=1}^{N}(-1)^tx_t/N\\ a_p &= 2 \frac{\sum_{t=1}^{N} x_t \cos(2 \pi p t/N)}{N}\\ b_p &= 2 \frac{\sum_{t=1}^{N} x_t \sin(2 \pi p t/N)}{N} \end{align}\]
- Fast Fourer transform (FFT) using complex numbers
used in signal processing (CD and MP3 players, mobile phones, …
Fast Fourier transform
Show the code
# create an arbitrary time series
set.seed(123)
n <- 360
t <- 0:(n-1)
x <- sin(t*2*pi/n) + rnorm(n, sd = 0.2)
plot(t, x, xlim = c(-10, 370))
# perform the FFT
p <- fft(x)
# invert the FFT for the main period only (keep parameters 1..3)
p[4:n] <- 0 # set higher order parameters to zero
x_sim <- fft(p, inverse = TRUE)
lines(t, 2 * Re(x_sim)/n - Re(p[1])/n, col = "blue", lwd = 4)
## perform FFT and invert it for all periods
p <- fft(x)
p[(n/2):n] <- 0 # set only the "redundant frequencies" to zero
x_sim <- fft(p, inverse = TRUE)
lines(t, 2 * Re(x_sim)/n - Re(p[1])/n, col = "red", lwd = 1)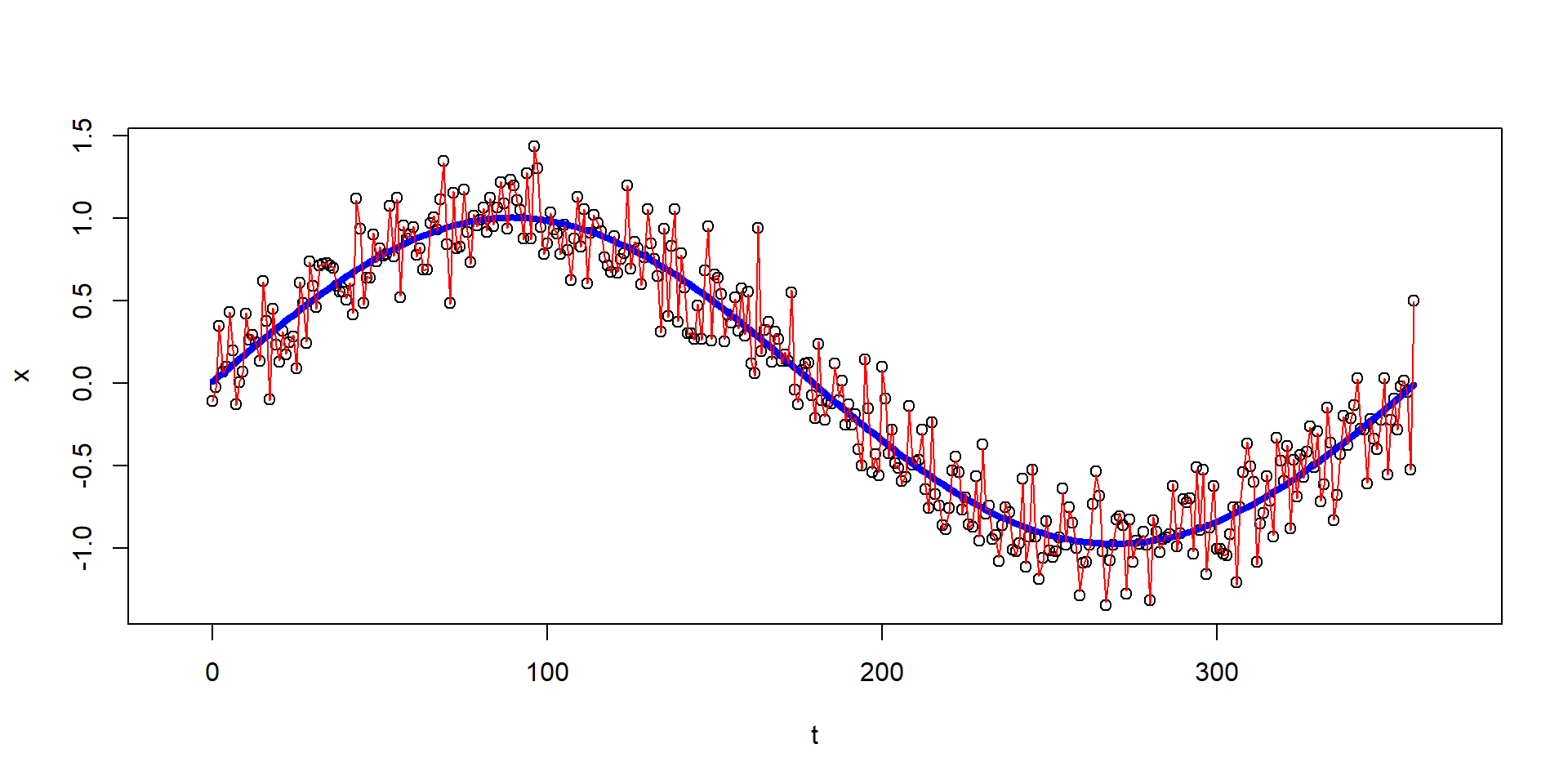
Automatic time series decomposition
Function decompose implements the classical approach with symmetric moving average.
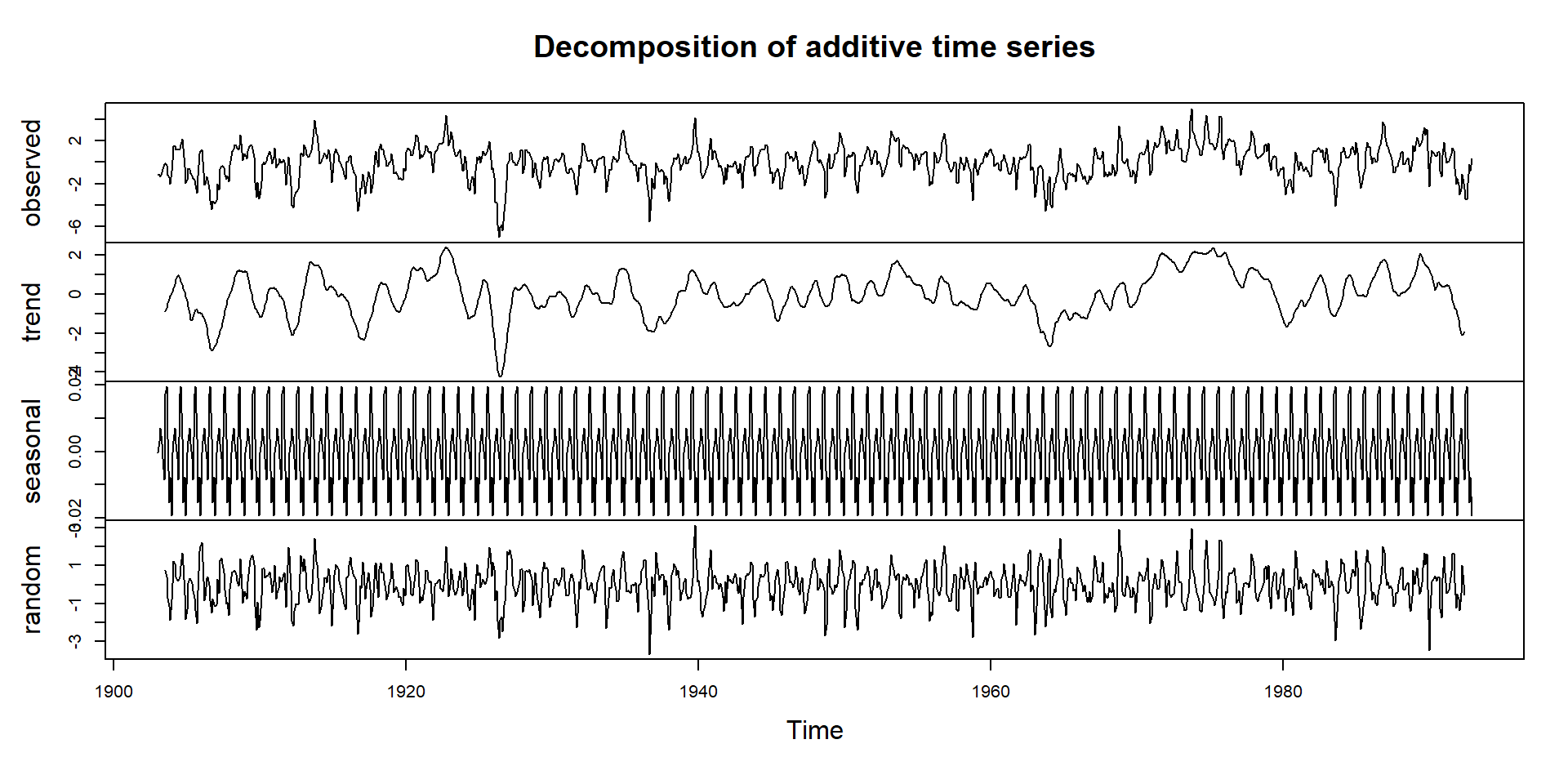
- In this data set the seasonal component possesses an additive character.
- In case of a multiplicative components, use
type = "multiplicative".
Automatic time series decomposition II
- function
stl(seasonal time series decomposition) (R. B. Cleveland et al., 1990) - uses a LOESS filter
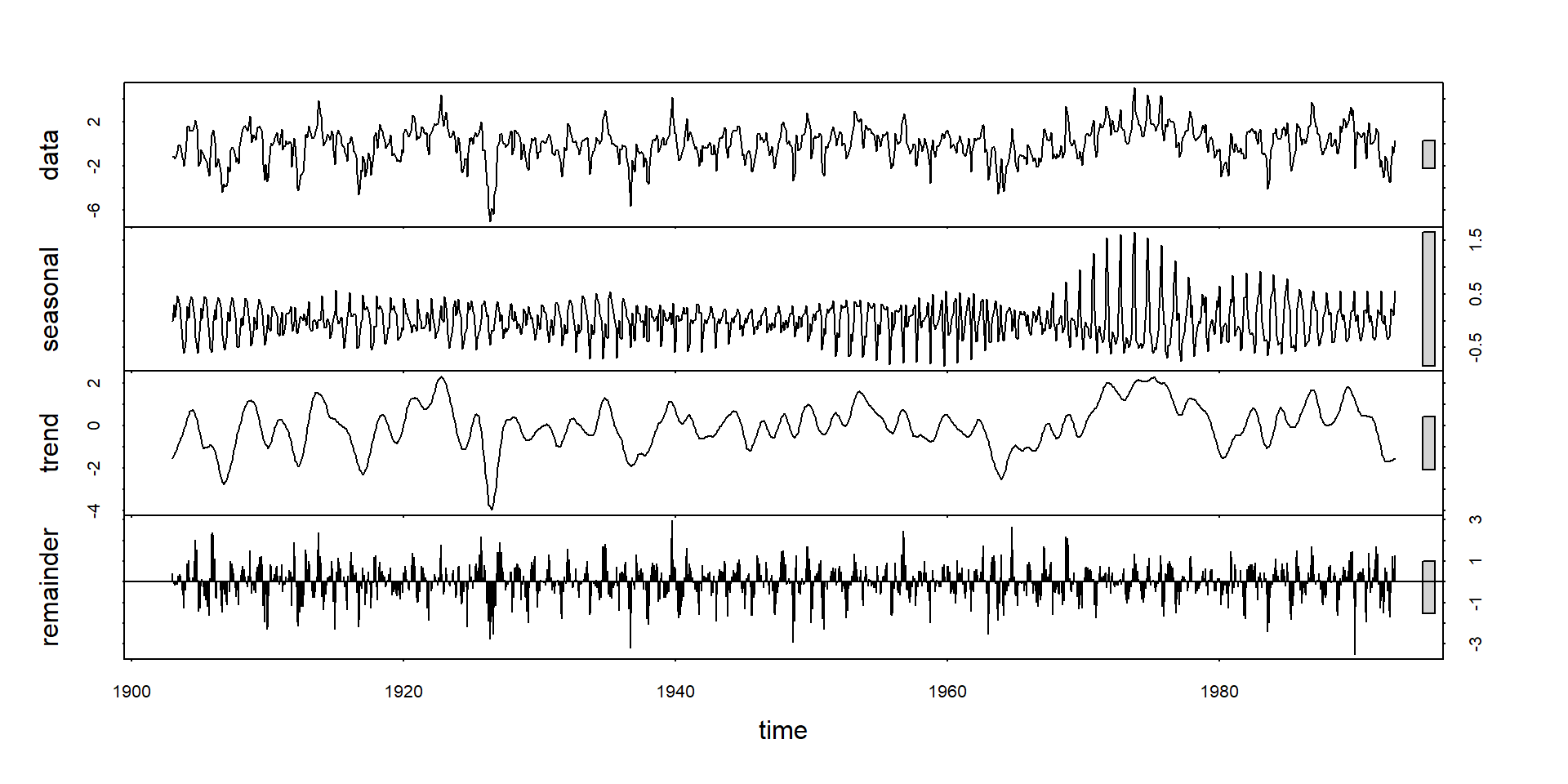
ARMA, ARIMA and SARIMA models
- based on autoregressive (AR) and moving average (MA) terms
- the “I” in ARIMA stands for differencing
- seasonal ARIMA models (SARIMA) consider seasonal dependency,
e.g. differencing with a lag of 12 months - very important techniques for analyzing time series and for forecasting
- for the interested: self-study, see Kleiber & Zeileis (2008) or Shumway & Stoffer (2019).
Example: SARIMA model for CO2 in the atmosphere
Show the code
## read data directly from NOAA
#co2 <- read_csv("https://gml.noaa.gov/webdata/ccgg/trends/co2/co2_mm_mlo.csv",
# skip = 40, show_col_types = FALSE)
## local version
co2 <- read_csv("../data/co2_mm_mlo.csv", skip=40, show_col_types = FALSE)
## year 1958 is incomplete, so let's start with 1959
co2 <- dplyr::filter(co2, year > 1958)
co2 |>
mutate(date=as_date(paste(year, month, 15, sep="."))) |>
ggplot(aes(date, average)) +
geom_line() + ylab(expression(CO[2]~"in the atmosphere (ppm)")) +
ggtitle("Mauna Loa Observatory, Hawaii, Monthly Averages") +
geom_smooth()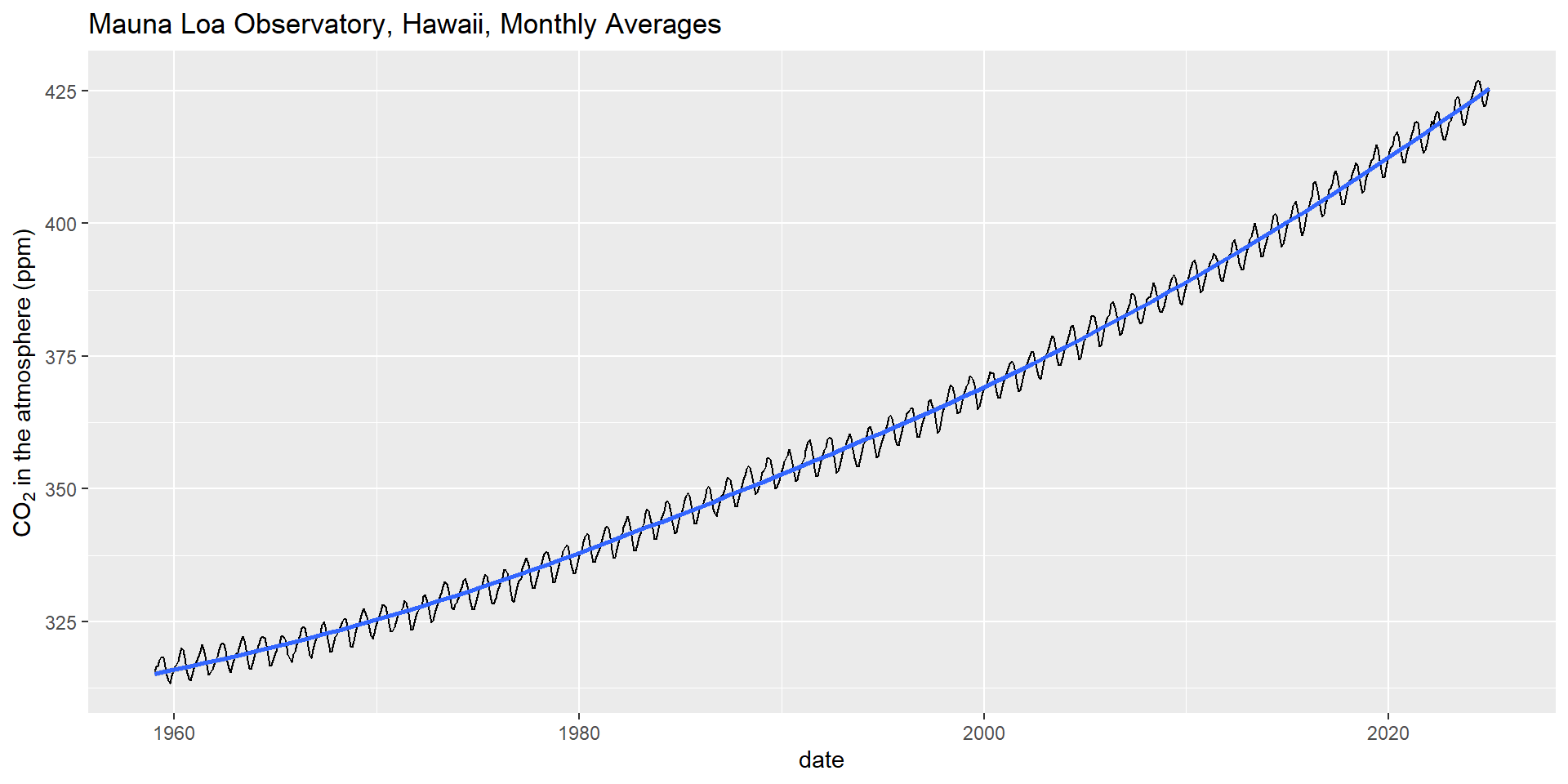
Fit SARIMA model to CO2 data
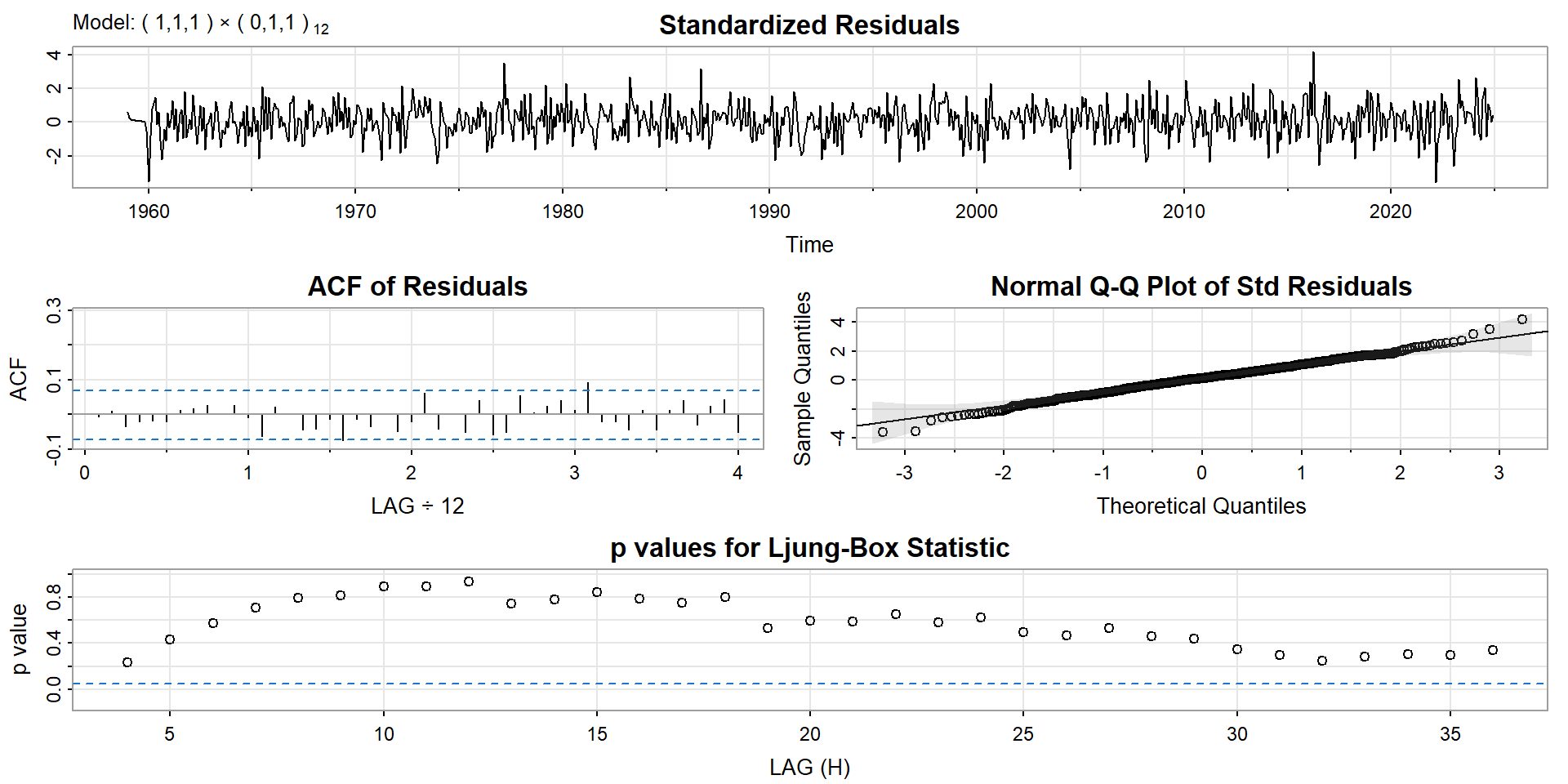
Mathematical details can be found in Shumway & Stoffer (2019).
SARIMA-forecast of CO2
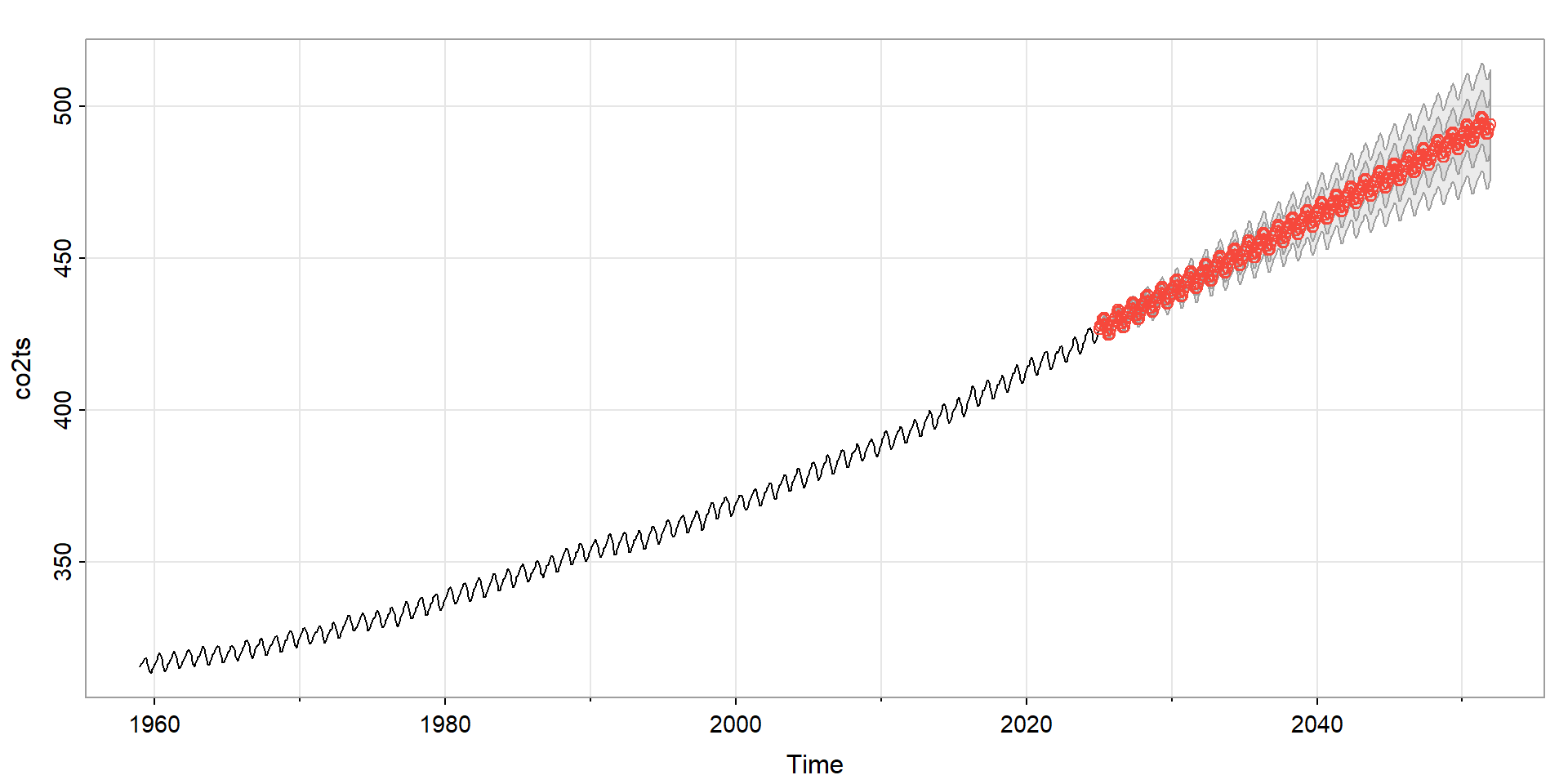
Mathematical details can be found in Shumway & Stoffer (2019).
Identification of structural breaks
Identification of structural breaks
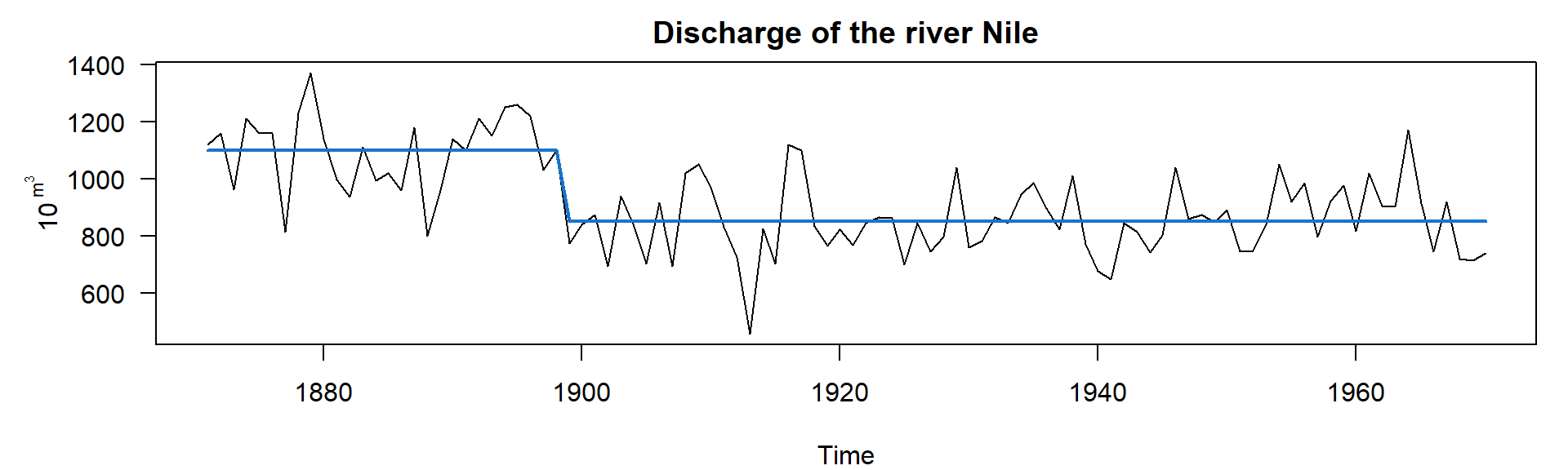
Structural break
If one or more statistical parameters are not constant over the whole length of a time series it is called a structural break. For instance a location parameter (e.g. the mean), a trend or another distribution parameter (such as variance or covariance) may change.
Testing for structural breaks
The package strucchange implements a number of tests for identification of structural changes or parameter instability of time series. Generally, two approaches are available: fluctuation tests and F-based tests. Fluctuation tests try to detect the structural instability with cumulative or moving sums (CUSUMs and MOSUMs).
The Nile data set
The Nile data set contains measurements of annual discharge of the Nile at Aswan from 1871 to 1970 (see help page ?Nile for data source):
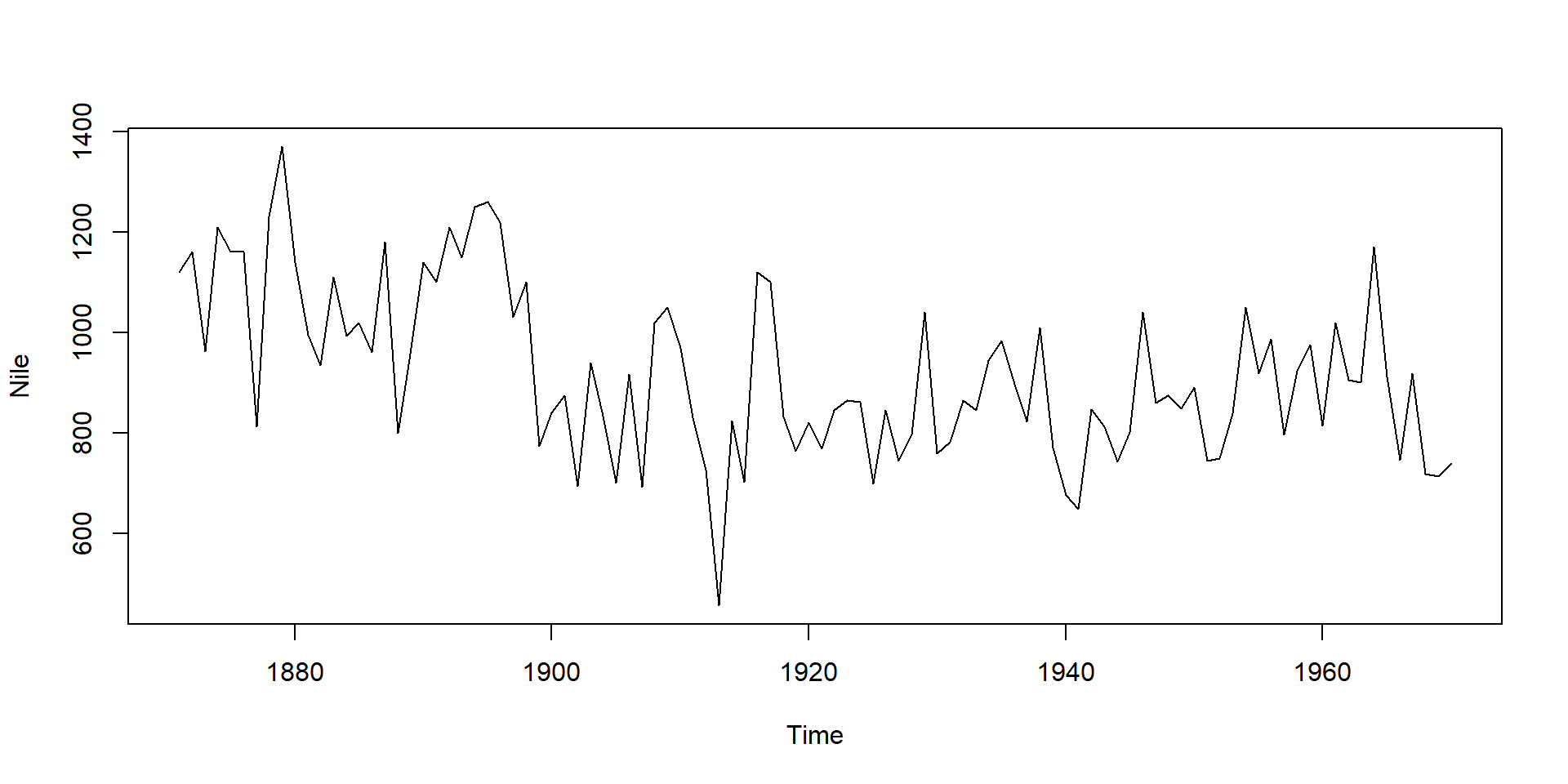
Test for existence of structural break
- Are there are periods with different flow?
- use of OLS-CUSUM (ordinary least squares, cumulative sum) or MOSUM tests (moving average sum)
efp= empirical fluctuation process,sctest= structural change test
OLS-based CUSUM test
data: ocus
S0 = 2.9518, p-value = 5.409e-08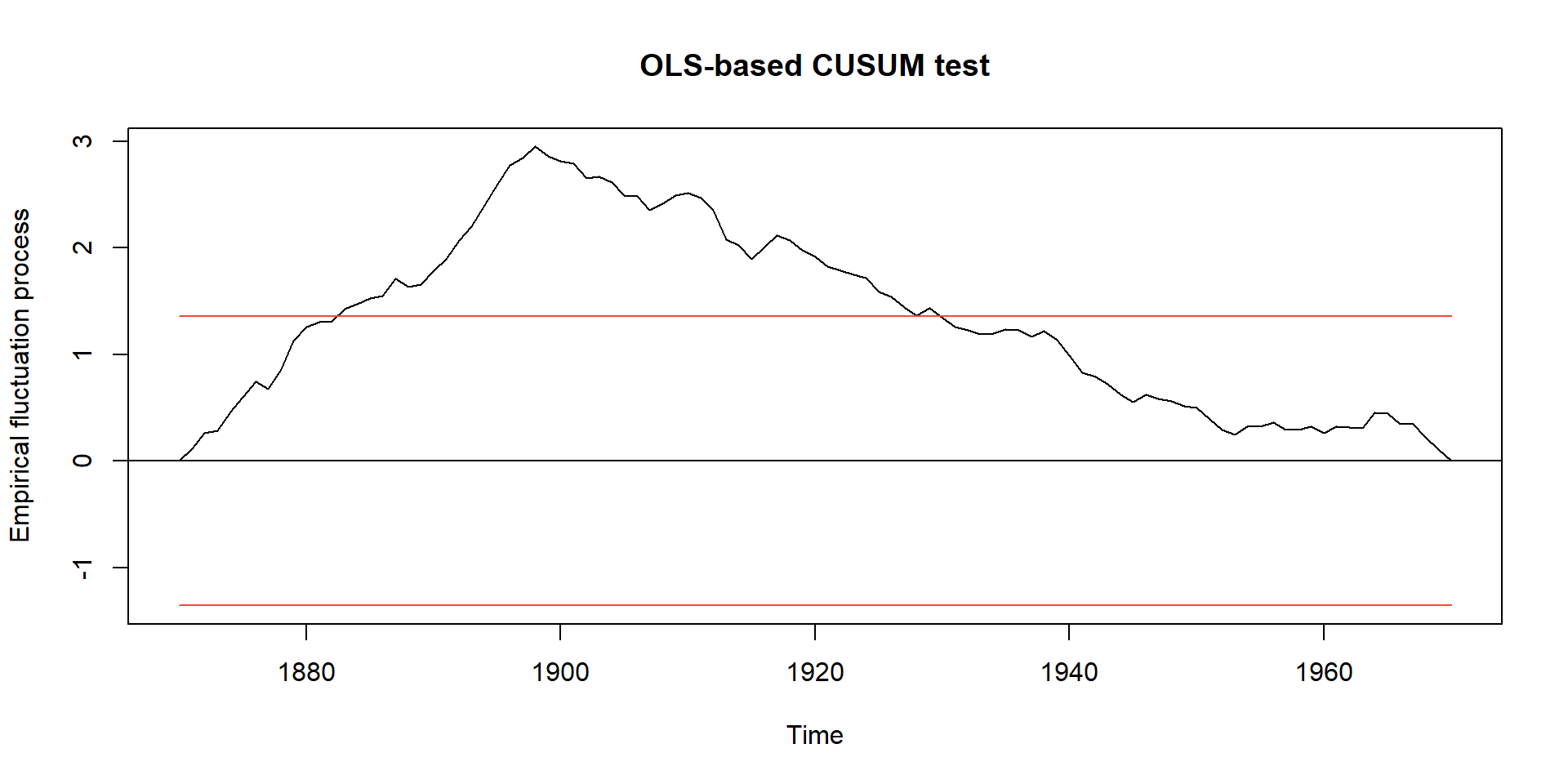
Breakpoint analysis
Purpose
- find structural breaks with respect to a specified linear model
- identify their number and location
- very general approach, allows different linear models, covariates, …
- we show the most simplest case here
Method
- employs a BIC-based model selection technique
- Which model is the best?
See also
Remember: model selection techniques
- model selection is a modern alternative to \(p\)-value based testing
- Based on the principle of parsimony:
- Models with more parameters fit better, but may contain unnecessary factors.
- \(\rightarrow\) Find an optimal compromise between model fit and complexity.
- Keep it as simple as possible, but not simpler.
- Multiple model candidates for the same phenomenon:
- Full model: includes all potential factors.
- Several reduced models, derived from the full model.
- Null model without explanatory factors.
- Select minimal adequate model (= “optimal”, “most parsimonious”).
More, see Johnson & Omland (2004)
Model selection with AIC and BIC
Models with more parameters fit better \(\leftrightarrow\) but more parameters (\(k\)) are “more complex”.
- Goodness of fit can be measured with likelihood \(L\)
(how likely are the data given a specific model). - Log likelihood: makes the problem additive.
- Penalty: penalises number of parameters (e.g. \(2 k\))
- AIC (Akaike Information Criterion):
\[ AIC = - 2 \ln(L) + 2 k \]
- Alternatively: BIC (Bayesian Information Criterion), considers sample size (\(n\)):
\[ BIC = - 2 \ln(L) + k \cdot \ln(n) \]
The model with smallest AIC (resp. BIC) is considered as “optimal” model.
Breakpoint analysis
Optimal (m+1)-segment partition:
Call:
breakpoints.formula(formula = Nile ~ 1)
Breakpoints at observation number:
m = 1 28
m = 2 28 83
m = 3 28 68 83
m = 4 28 45 68 83
m = 5 15 30 45 68 83
Corresponding to breakdates:
m = 1 1898
m = 2 1898 1953
m = 3 1898 1938 1953
m = 4 1898 1915 1938 1953
m = 5 1885 1900 1915 1938 1953
Fit:
m 0 1 2 3 4 5
RSS 2835157 1597457 1552924 1538097 1507888 1659994
BIC 1318 1270 1276 1285 1292 1311Notes
- computationally intensive
- consider to adapt model and parameter
h, see help page
Likelihood profile: \(\rightarrow\) optimal number of breaks?
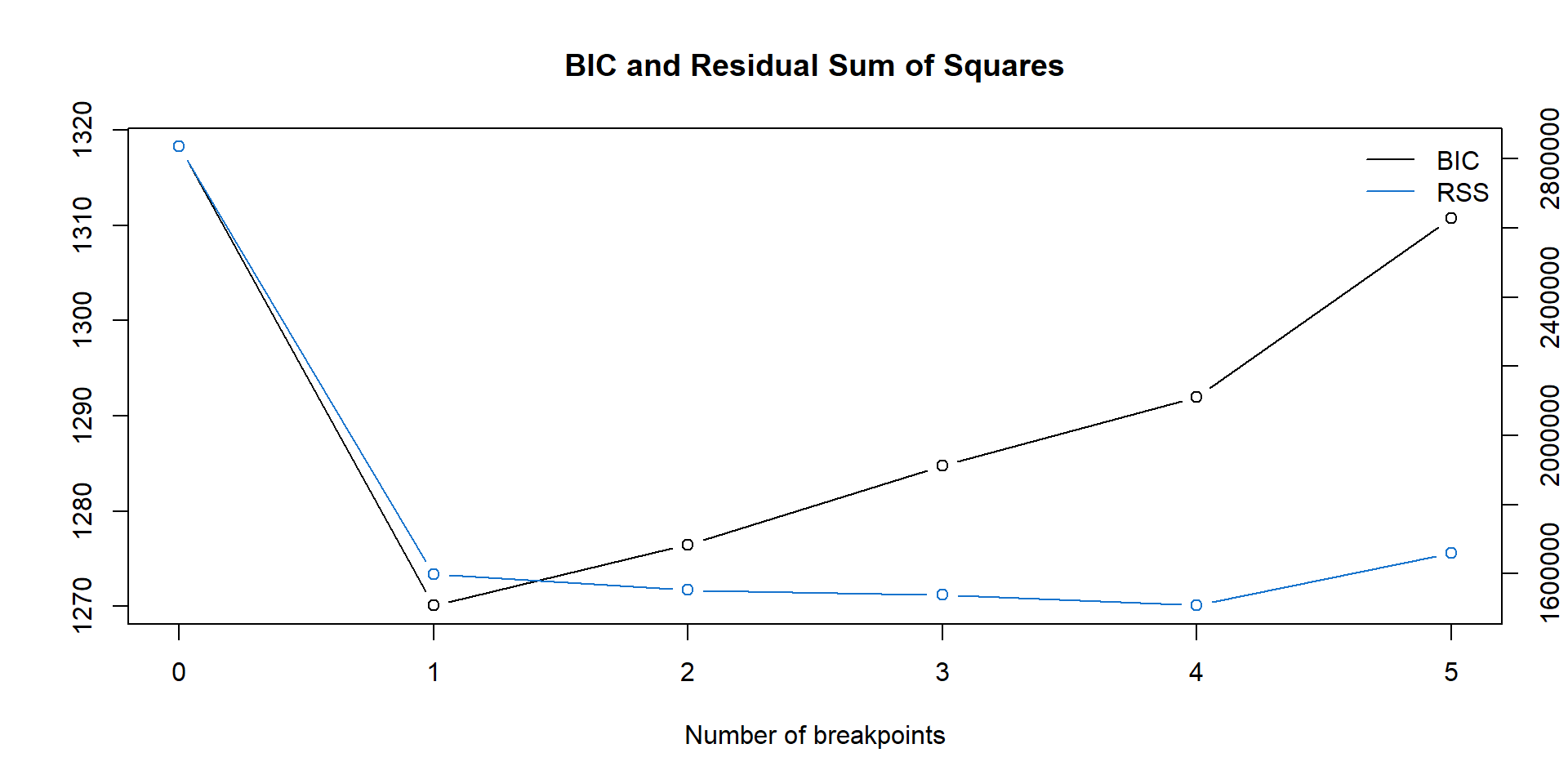
- RSS (residual sum of squares) shows goodness of fit. The smaller the better.
- Penalty = 2 \(\cdot\) number of breakpoints (not shown).
- Minimum BIC indicates optimal model.
Plot breakpoints and confidence interval
## fit null hypothesis model and model with 1 breakpoint
fm0 <- lm(Nile ~ 1)
fm1 <- lm(Nile ~ breakfactor(bp.nile, breaks = 1))
plot(Nile)
lines(ts(fitted(fm0), start = 1871), col = 3)
lines(ts(fitted(fm1), start = 1871), col = 4)
lines(bp.nile)
## confidence interval
ci.nile <- confint(bp.nile)
#ci.nile # output numerical results
lines(ci.nile)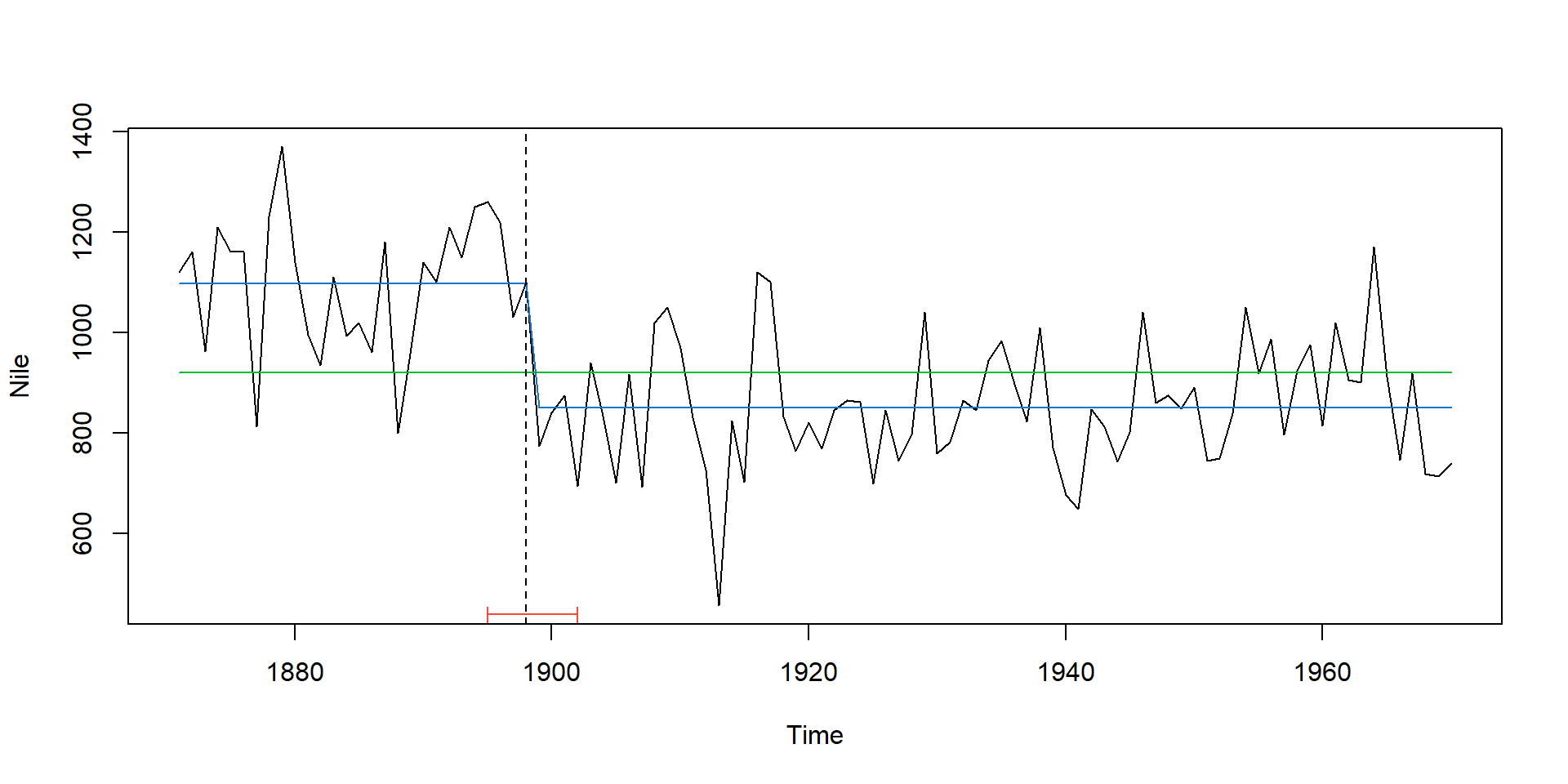
Test significance of breakpoints
Likelihood ratio test
Analysis of Variance Table
Model 1: Nile ~ 1
Model 2: Nile ~ breakfactor(bp.nile, breaks = 1)
Res.Df RSS Df Sum of Sq F Pr(>F)
1 99 2835157
2 98 1597457 1 1237700 75.93 7.439e-14 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1BIC based comparison
AIC based comparison
\(\rightarrow\) model with structural break in 1898 is significantly better than the null model.
Diagnostics
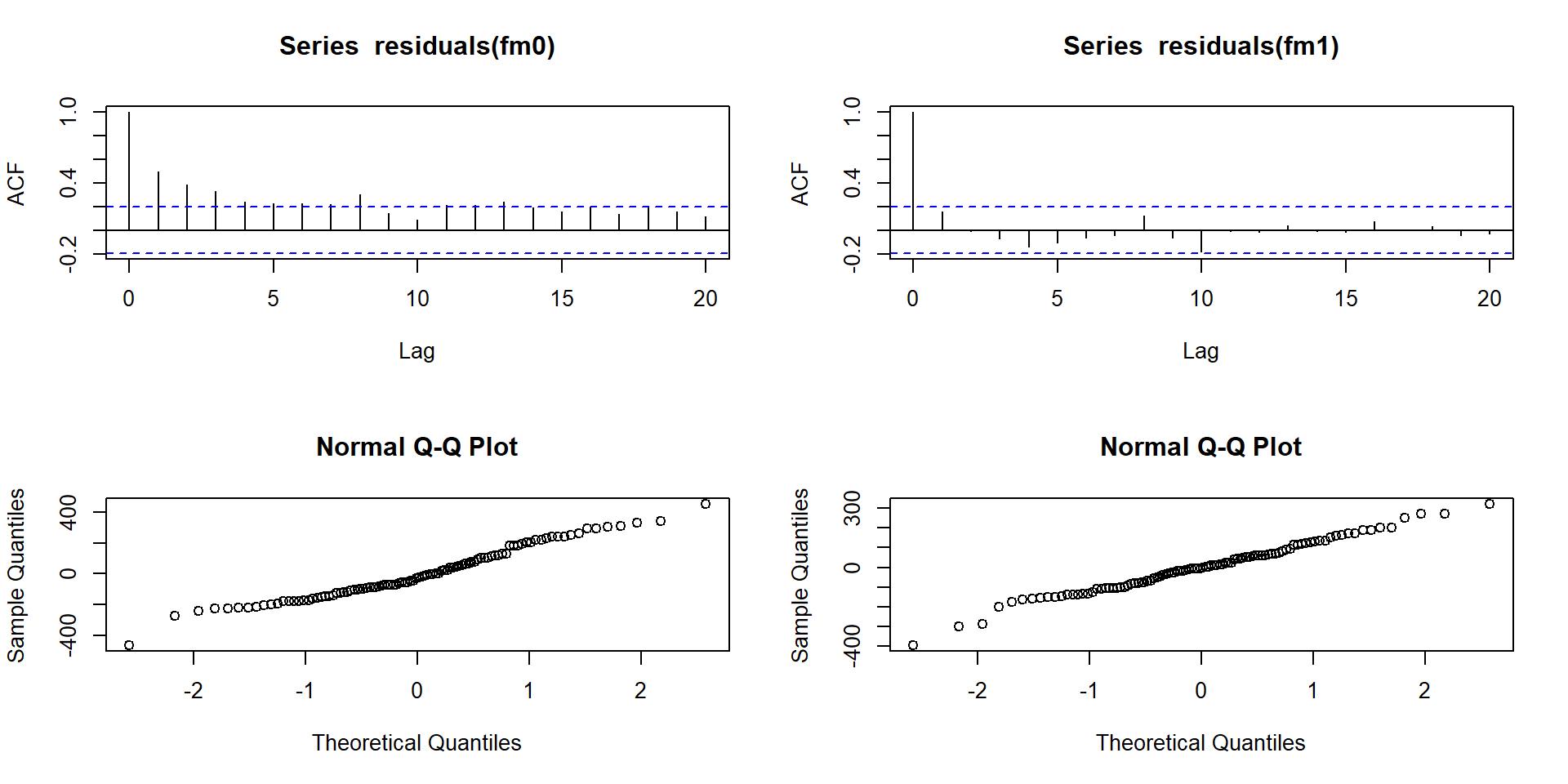
Comparison to segmented regression
Show the code
library(segmented)
# 1. Create sample data with a breakpoint
# formula changes at x = 50
set.seed(4123)
x <- 1:100
df <- data.frame(
x = x,
y = c(2 * x[1:50], 100 + 0.5 * x[51:100]) + rnorm(100, 0, 10)
)
# 2. Fit a standard linear model first
m1 <- lm(y ~ x, data = df)
# 3. Fit the segmented model
# psi = 50 is an initial guess for the breakpoint
m2 <- segmented(m1, seg.Z = ~ x, psi = 50)
# 4. Visualization
plot(y ~ x, data = df, pch = 16, col="gray")
abline(m1, col="blue", lwd=2, lty="dashed")
plot(m2, add = TRUE, col = "red", lwd = 4)
# ===================================================
# 5. Comparison with a strucchange model
library(strucchange)
bp <- breakpoints(y ~ x, data = df, breaks = 1)
fac <- breakfactor(bp)
m3 <- lm(y ~ x * fac, data = df)
# Split data to avoid the vertical connecting line
df$p <- predict(m3)
s1 <- subset(df, fac == "segment1")
s2 <- subset(df, fac == "segment2")
lines(p ~ x, data = s1, lwd = 2, col = "black")
lines(p ~ x, data = s2, lwd = 2, col = "black")
# 6. Add legend
legend("topleft",
legend = c("Linear Model", "Segmented (Connected)", "Strucchange (Jump)"),
col = c("blue", "red", "black"),
lwd = c(2, 4, 2),
lty = c("dashed", "solid", "solid"),
bg = "white")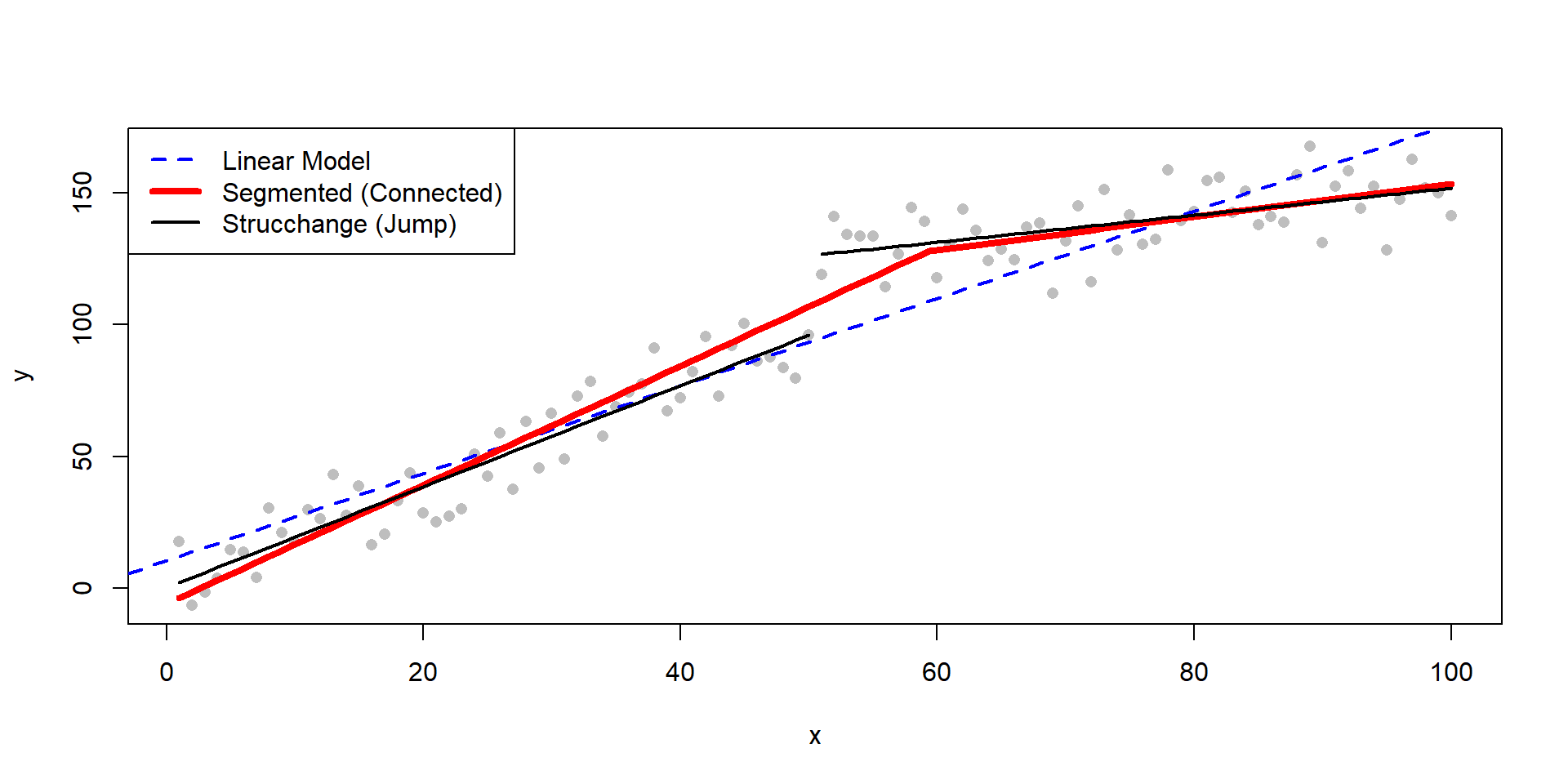
Model results
Estimated changepoint and slopes
***Regression Model with Segmented Relationship(s)***
Call:
segmented.lm(obj = m1, seg.Z = ~x, psi = 50)
Estimated Break-Point(s):
Est. St.Err
psi1.x 59.382 2.964
Coefficients of the linear terms:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -5.95146 3.12427 -1.905 0.0598 .
x 2.25394 0.09057 24.887 <2e-16 ***
U1.x -1.62792 0.18070 -9.009 NA
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 11.85 on 96 degrees of freedom
Multiple R-Squared: 0.947, Adjusted R-squared: 0.9453
Boot restarting based on 6 samples. Last fit:
Convergence attained in 2 iterations (rel. change 9.5841e-12)Lists the slopes of each segment
Comparison: strucchange vs. segmented
- Continuity
segmentedmodels are connectedstrucchangeallows vertical jumps at the breakpoint
- Parameter Shifts
segmentedusually focuses on a change in slopestrucchangeallows every parameter (intercept and all slopes) to change simultaneously
- Estimation
segmenteduses an iterative approach (requires start value)strucchangeuses dynamic programming to find the globally optimal break locations.
When to use “jumps”
- Appropriate for sudden “shocks”, (e.g., new dam, market crash).
- Inappropriate for continuous processes (e.g., plant growth, aging), where a sudden jump is physically or biologically impossible.