5.5 + c(-1, 1) * qt(0.975, 10-1) * 1/sqrt(10)[1] 4.784643 6.215357Applied Statistics – A Practical Course
2025-11-20
A statistical hypothesis test is a method of statistical inference.
adapted from: https://en.wikipedia.org/wiki/Statistical hypothesis testing
In case of relative mean differences, the relative effect size is:
\[ \delta = \frac{\bar{\mu}_1-\bar{\mu}_2}{\sigma}=\frac{\Delta}{\sigma} \]
with:
\(H_0\) null hypothesis: two populations are not different with respect to a certain property.
\(H_a\) alternative hypothesis (experimental hypothesis): existence of a certain effect.
“Not significant” means either no effect or sample size too small!
Note: Different meaning of significance (\(H_0\) unlikely) and relevance (effect large enough to play a role in practice).
The interpretation of the p-value was often confused in the past, even in statistics textbooks, so it is good to refer to a clear definition:
The p-value is defined as the probability of obtaining a result equal to or ‘more extreme’ than what was actually observed, when the null hypothesis is true.
Hubbard (2004) Alphabet Soup: Blurring the Distinctions Between p’s and a’s in Psychological Research, Theory Psychology 14(3), 295-327. DOI: 10.1177/0959354304043638
| Reality | Decision of the test | correct? | probability |
|---|---|---|---|
| \(H_0\) = true | significant | no | \(\alpha\)-error |
| \(H_0\) = false | not significant | no | \(\beta\)-error |
| \(H_0\) = true | not significant | yes | \(1-\alpha\) |
| \(H_0\) = false | significant | yes | \(1-\beta\) (power) |
1.\(H_0\) falsely rejected (error of the first kind or \(\alpha\)-error)
2.\(H_0\) falsely retained (error of the second kind or \(\beta\)-error)
Use in practice
Significance is not the only important. Focus also on effect size and relevance!
Statistical significance means that the null hypothesis \(H_0\) is unlikely in a statistical sense.
Practical relevance (sometimes called “practical significance”) means that the effect size is large enough to play a role in practice.
This means that whether an effect can be relevant or not depends on its effect size and the field of application.
Let’s for example consider a vaccination. If a vaccine had a significant effect in a clinical test, but protected only 10 out of 1000 people, one would not consider this effect as relevant and not produce this vaccine.
On the other hand, even small effects can be relevant. So if a toxic substance would have an effect on 1 out of 1000 people to produce cancer, we would consider this as relevant. To detect this as a significant effect would need an epidemiological study with a large number of people. But as it is highly relevant, it is worth the effort.
A p-value measures the probability that a purely random effect would be equally or more extreme than an observed effect if the null hypothesis is true.
Significant means the results are unlikely if there were no real effect.
Not significant doesn’t mean “no effect”.
Non-significant results suggest the need for further research, e.g.:
Don’t focus on p-values alone. Never forget to report also sample size, effect size and relevance of your results.
With large datasets:
The p-value remains an important tool in statistics, but misuse can lead to misinterpretation.
\[ CI = \bar{x} \pm t_{1-\alpha/2, n-1} \cdot s_{\bar{x}} \] with \[ s_{\bar{x}} = \frac{s}{\sqrt{n}} \qquad \text{(standard error)} \]
Different ways of calculation shown at the next slides
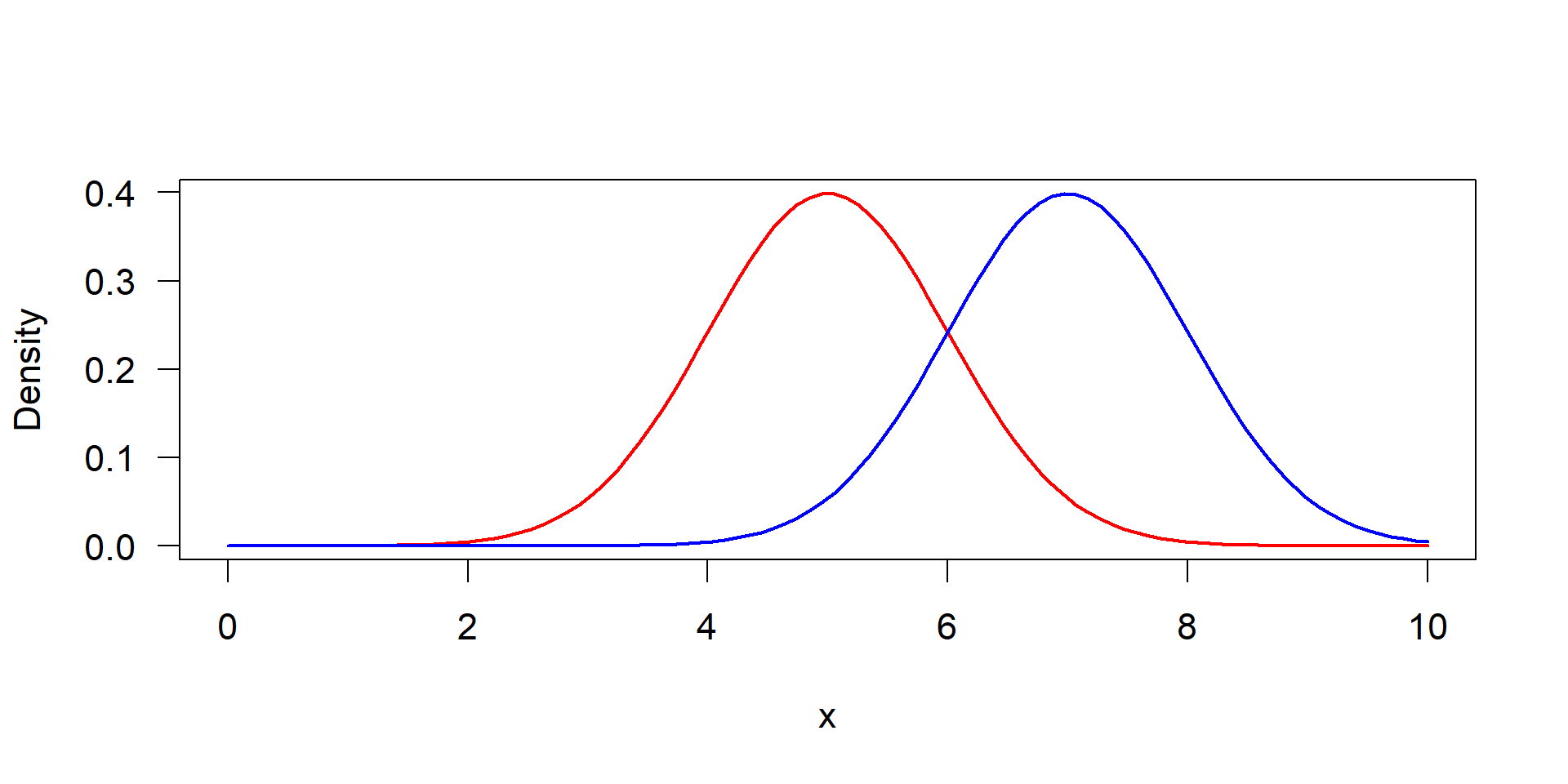
Visualization of a one-sample t-test. Left: original distribution of the data measured by standard deviation, right: distribution of mean values, measured by its standard error.
\[ s_{\bar{x}} = \frac{s}{\sqrt{n}} \qquad \text{(standard error)} \]
The test is based on the distribution of the means, not distribution of original data.
Sample: \(n=10, \bar{x}=5.5, s=1\) and \(\mu=5\)
Let \(\alpha = 0.05\), we get a two-sided 95% confidence interval with:
\[\bar{x} \pm t_{0,975, n-1} \cdot \frac{s}{\sqrt{n}}\]
Check if \(\mu=5.0\) is in this interval?
Yes, it is inside \(\Rightarrow\) difference not significant.
\[ t_{obs} = |\bar{x}-\mu | \cdot \frac{1}{s_{\bar{x}}} = \frac{|\bar{x}-\mu |}{s} \cdot \sqrt{n} = \frac{|5.5 -5.0|}{1.0} \cdot \sqrt{10} \]
We can calculate this in R:
Comparison: \(1.58 < 2.26\) \(\Rightarrow\) no significant difference between \(\bar{x}\) and \(\mu\).
pt) instead of table lookupThis p-value = 0.1483047 is greater than \(0.05\) so we consider the difference as not significant.
FAQ: less than or greater than?
| p-value | \(\text{p-value} < \alpha\) | null hypothesis unlikely | significant |
| test statistic | \(t_{obs} > t_{1-\alpha/2, n-1}\) | effect exceeds confint. | significant |
The same can be done much easier with the computer in R.
Let’s assume we have a sample with \(\bar{x}=5, s=1\):
## define sample
x <- c(5.5, 3.5, 5.4, 5.3, 6, 7.2, 5.4, 6.3, 4.5, 5.9)
## perform one-sample t-test
t.test(x, mu=5)
One Sample t-test
data: x
t = 1.5811, df = 9, p-value = 0.1483
alternative hypothesis: true mean is not equal to 5
95 percent confidence interval:
4.784643 6.215357
sample estimates:
mean of x
5.5 The test returns the observed t-value, the 95% confidence interval and the p-value.
An important difference is, that this method needs the original data, while the other methods need only mean, standard deviation and sample size.
The two-sample t-test compares two independent samples:
x1 <- c(5.3, 6.0, 7.1, 6.4, 5.7, 4.9, 5.0, 4.6, 5.7, 4.0, 4.5, 6.5)
x2 <- c(5.8, 7.1, 5.8, 7.0, 6.7, 7.7, 9.2, 6.0, 7.2, 7.8, 7.8, 5.7)
t.test(x1, x2)
Welch Two Sample t-test
data: x1 and x2
t = -3.7185, df = 21.611, p-value = 0.001224
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-2.3504462 -0.6662205
sample estimates:
mean of x mean of y
5.475000 6.983333 \(H_0\) \(\mu_1 = \mu_2\)
\(H_a\) the two means are different
test criterion
\[ t_{obs} =\frac{|\bar{x}_1-\bar{x}_2|}{s_{tot}} \cdot \sqrt{\frac{n_1 n_2}{n_1+n_2}} \]
pooled standard deviation
\[ s_{tot} = \sqrt{{({n}_1 - 1)\cdot s_1^2 + ({n}_2 - 1)\cdot s_2^2 \over ({n}_1 + {n}_2 - 2)}} \]
assumptions: independence, equal variances, approximate normal distribution
Known as t-test for samples with unequal variance, works also for equal variance!
Test criterion:
\[ t = \frac{\bar{x}_1 - \bar{x}_2}{\sqrt{s^2_{\bar{x}_1} + s^2_{\bar{x}_2}}} \]
Standard error of each sample:
\[ s_{\bar{x}_i} = \frac{s_i}{\sqrt{n_i}} \] Corrected degrees of freedom:
\[ \text{df} = \frac{\frac{s^2_1}{n_1} + \frac{s^2_2}{n_2}}{\frac{s^4_1}{n^2_1(n_1-1)} + \frac{s^4_2}{n^2_2(n_2-1)}} \]
… is just the default method of the t.test-function.
\(H_0\): \(\sigma_1^2 = \sigma_2^2\)
\(H_a\): variances unequal
Test criterion:
\[F = \frac{s_1^2}{s_2^2} \]
Example:
\(\Rightarrow\) \(F_{9, 4, \alpha=0.975} = 8.9 > 4 \quad\rightarrow\) not significant
Bartlett’s test:
Bartlett test of homogeneity of variances
data: list(x1, x2, x3)
Bartlett's K-squared = 7.7136, df = 2, p-value = 0.02114
Fligner-Killeen test (recommended):
Traditional procedure:
var.test(x, y)t.test(x, y, var.equal=TRUE)t.test(x, y) (= Welch test)Modern recommendation (preferred):
t.test(x, y)sometimes also called “t-test of dependent samples”
examples: left arm / right arm; before / after
is essentially a one-sample t-test of pairwise differences against \(\mu=0\)
reduces the influence of individual differences (“covariates”) by focusing on the change within each pair
Two Sample t-test
data: x1 and x2
t = -1.372, df = 8, p-value = 0.2073
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-4.28924 1.08924
sample estimates:
mean of x mean of y
4.0 5.6 p=0.20, not significant
Paired t-test
data: x1 and x2
t = -4, df = 4, p-value = 0.01613
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
-2.710578 -0.489422
sample estimates:
mean difference
-1.6 p=0.016, significant
It can be seen that the paired t-test has a greater discriminatory power in this case.
Basic principle: Count of so-called “inversions” of ranks, where samples overlap
\[\begin{align*} U_A &= m \cdot n + \frac{m (m + 1)}{2} - \sum_{i=1}^m R_A \\ U_B &= m \cdot n + \frac{n (n + 1)}{2} - \sum_{i=1}^n R_B \\ U &= \min(U_A, U_B) \end{align*}\]
wilcox.exact with correction if sample has ties.A <- c(1, 3, 4, 5, 7)
B <- c(6, 8, 9, 10, 11)
wilcox.test(A, B) # use optional argument `paired = TRUE` for paired data.
Wilcoxon rank sum exact test
data: A and B
W = 1, p-value = 0.01587
alternative hypothesis: true location shift is not equal to 0Mann-Whitney - Wilcoxon-test with tie correction
Gamma(2.3, 1)Gamma(1.0, 1)Key Idea
The algorithm (by example of a mean difference)
\(\rightarrow\) Can be used to arbitrary statistical parameters and experimental designs.
Let \(\Delta_{obs}\) be \(1.5\) in our example, then \(\Rightarrow\) \(p= 0.01\).
How many replicates will I need?
Depends on:
\[\delta=\frac{(\bar{x}_1-\bar{x}_2)}{s}\]
The smaller \(\alpha\), \(n\) and \(\delta\), the bigger the type II (\(\beta\)) error.
The \(\beta\)-error is the probability to overlook effects despite of their existence.
Power (\(1-\beta\)) is the probability that a test is significant if an effect exists.
Formula for minimum sample size in the one-sample case:
\[ n = \bigg(\frac{z_\alpha + z_{1-\beta}}{\delta}\bigg)^2 \]
qnorm) of the standard normal distribution for \(\alpha\) and for \(1-\beta\)Example
Two-tailed test with \(\alpha=0.025\) and \(\beta=0.2\)
\(\rightarrow\) \(z_\alpha = 1.96\), \(z_\beta=0.84\), then:
\[ n= (1.96 + 0.84)^2 \cdot 1/\delta^2 \approx 8 /\delta^2 \]
\(\delta = 1.0\cdot \sigma\) \(\qquad\Rightarrow\) n > 8
\(\delta = 0.5\cdot \sigma\) \(\qquad\Rightarrow\) n > 32
The power of a t-test, or the minimum sample size, can be calculated with: power.t.test():
Two-sample t test power calculation
n = 5
delta = 0.5
sd = 1
sig.level = 0.05
power = 0.1038399
alternative = two.sided
NOTE: n is number in *each* group\(\rightarrow\) power = 0.10
For a weak effect of \(0.5\sigma\) we need a sample size of \(n\ge64\) in each group:
\(\Rightarrow\) we need either a large sample size or a strong effect.
# population parameters
n <- 10
xmean1 <- 50; xmean2 <- 55
xsd1 <- xsd2 <- 10
alpha <- 0.05
nn <- 1000 # number of test runs in the simulation
a <- b <- 0 # initialize counters
for (i in 1:nn) {
# create random numbers
x1 <- rnorm(n, xmean1, xsd1)
x2 <- rnorm(n, xmean2, xsd2)
# results of the t-test
p <- t.test(x1,x2,var.equal = TRUE)$p.value
if (p < alpha) {
a <- a+1
} else {
b <- b+1
}
}
print(paste("a=", a, ", b=", b, ", a/n=", a/nn, ", b/n=", b/nn))Nominal variables
Ordinal variables
Metric scales
Example: Occurence of Daphnia (water flea) in a lake:
| Clone | Upper layer | Deep layer |
|---|---|---|
| A | 50 | 87 |
| B | 37 | 78 |
| C | 72 | 45 |
| Clone A | Clone B | Clone C | Sum \(s_i\) | |
|---|---|---|---|---|
| Upper layer | 50 | 37 | 72 | 159 |
| Lower layer | 87 | 78 | 45 | 210 |
| Sum \(s_j\) | 137 | 115 | 117 | \(n=369\) |
| Clone A | Clone B | Clone C | Sum \(s_i\) | |
|---|---|---|---|---|
| Upper layer | 59.0 | 49.6 | 50.4 | 159 |
| Lower layer | 78.0 | 65.4 | 66.6 | 210 |
| Sum \(s_j\) | 137 | 115 | 117 | \(n=369\) |
Test statistic \(\hat{\chi}^2 = \sum_{i, j} \frac{(O_{ij} - E_{ij})^2}{E_{ij}}\)
Compare with critical \(\chi^2\) from table with \((n_{row} - 1) \cdot (n_{col} - 1)\) df.
Organize data in a matrix with 3 rows (for the clones) and 2 columns (for the depths):
\(\rightarrow\) significant correlation between the clones and vertical distribution in the lake.
Chi-squared test for given probabilities
data: obsfreq
X-squared = 13.647, df = 8, p-value = 0.09144
Chi-squared test for given probabilities with simulated p-value (based
on 1000 replicates)
data: obsfreq
X-squared = 13.647, df = NA, p-value = 0.0959\[ T = n \omega^2 = \frac{1}{12n} + \sum_{i=1}^n \left[ \frac{2i-1}{2n}-F(x_i) \right]^2 \]
library(dgof)
obsfreq <- c(1, 1, 6, 2, 2, 5, 8, 6, 3)
## CvM-test needs individual values, not class frequencies
x <- rep(1:length(obsfreq), obsfreq)
x [1] 1 2 3 3 3 3 3 3 4 4 5 5 6 6 6 6 6 7 7 7 7 7 7 7 7 8 8 8 8 8 8 9 9 9## create a cumulative function with equal probability of all cases
cdf <- stepfun(1:9, cumsum(c(0, rep(1/9, 9))))
cdf <- ecdf(1:9)
## perform the test
cvm.test(x, cdf)
Cramer-von Mises - W2
data: x
W2 = 0.51658, p-value = 0.03665
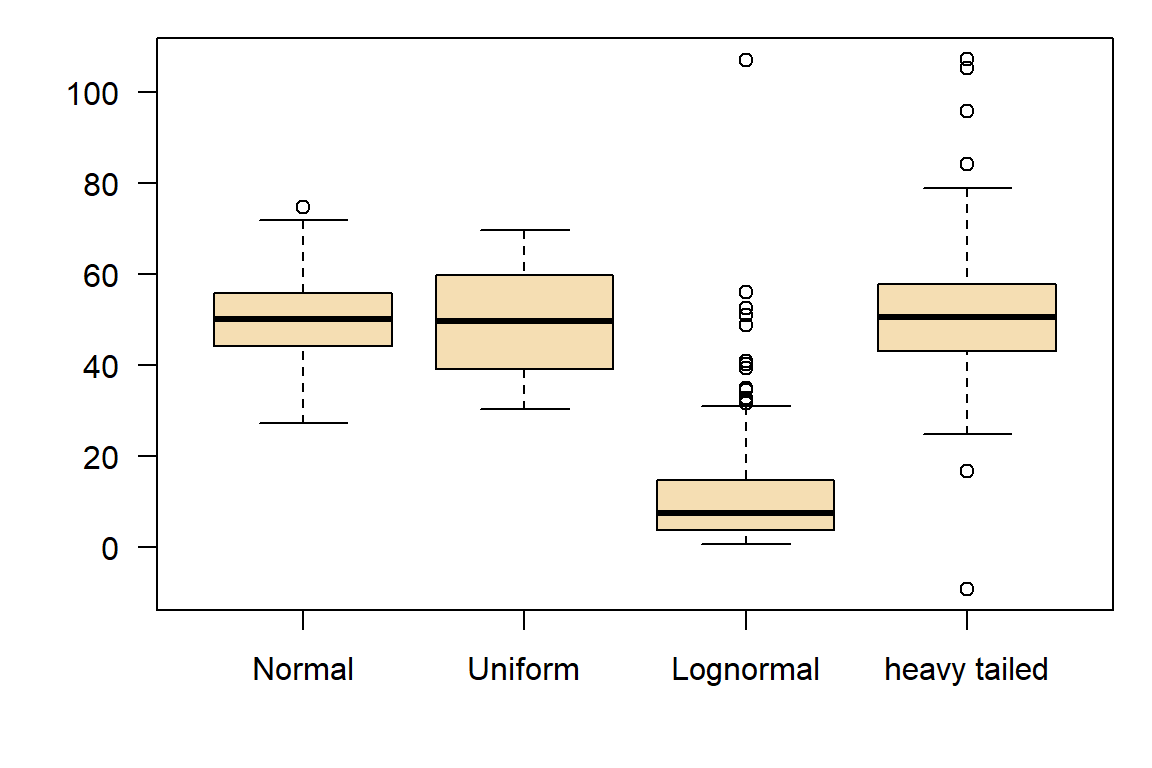
alternative hypothesis: Two.sidedSometimes we want to know whether a data set belongs to a specific type of distribution. Though this sounds easy, it appears quite difficult for theoretical reasons:
This is in fact impossible, because “not significant” means only that a potential effect is either not existent or just too small to be detected. On the opposite, “significantly different” includes a certain probability of false positives.
However, most statistical tests do not require perfect agreement with a certain distribution:
Philosophical problem: We want to keep the \(H_0\)!
Think first
Inherent non-normality
Some types of data, such as count data (e.g., number of occurrences) and binary data (e.g., yes/no), are inherently non-normal.
\(\rightarrow\) Aim: tests if a sample conforms to a normal distribution
\(\rightarrow\) the \(p\)-value is greater than 0.05, so we would keep \(H_0\) and conclude that nothing speaks against acceptance of the normal
Interpration of the Shapiro-Wilks-test needs to be done with care:
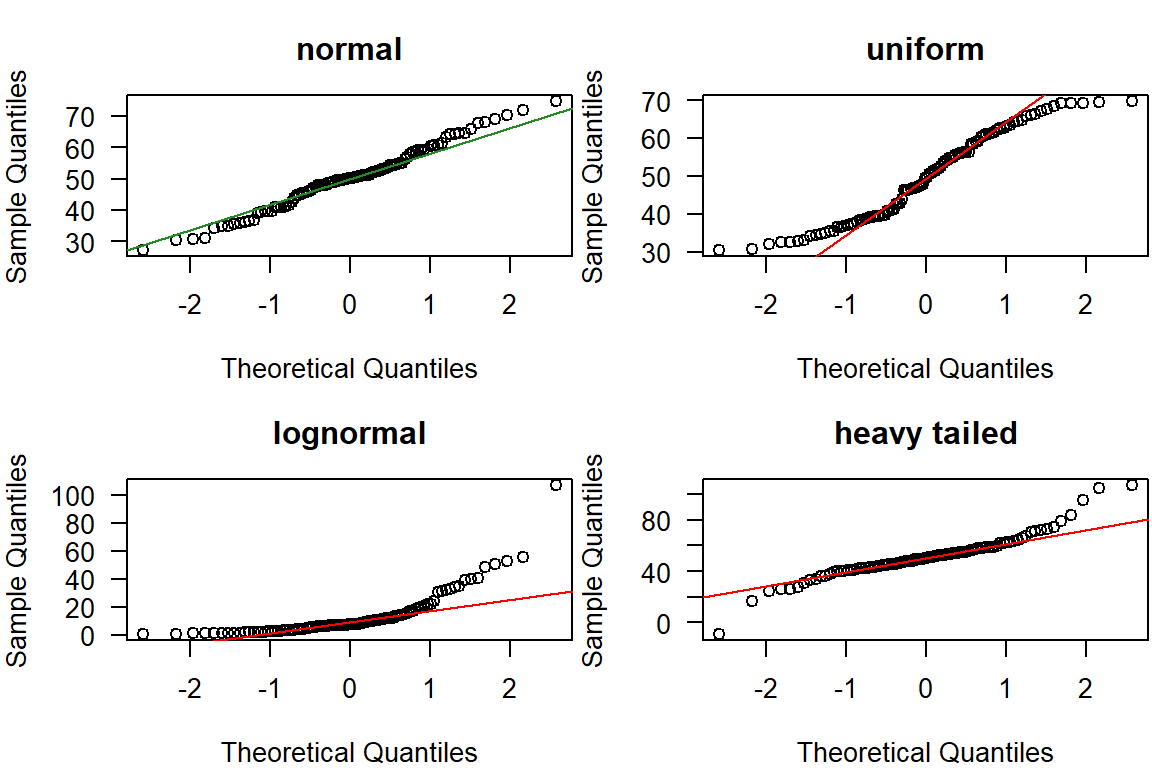
In some disciplines, such as hydrology, it is occasionally necessary to know which distribution type best describes a dataset. This is especially critical for Extreme Value Analysis (e.g., the 100-year flood), as the Central Limit Theorem (CLT) does not apply here.
Procedure
Transformations for right-skewed data
Transformations for count data
\(\rightarrow\) consider a GLM with family Poisson or quasi-Poisson instead
Ratios and percentages values between (0, 1)
\(\rightarrow\) consider a GLM with family binomial instead
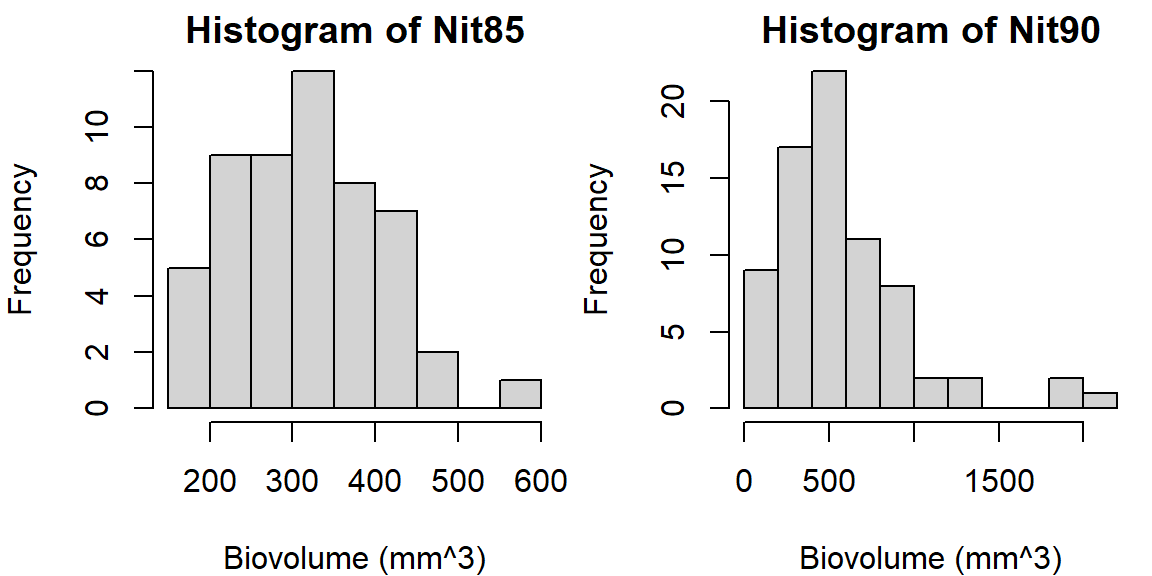
\[ y' = \begin{cases} \frac{y^\lambda -1}{\lambda} & | & \lambda \ne 0\\ \log(y) & | & \lambda =0 \end{cases} \] In some practical cases, one can simply use \(y^\lambda\) instead of \(\frac{y^\lambda -1}{\lambda}\).
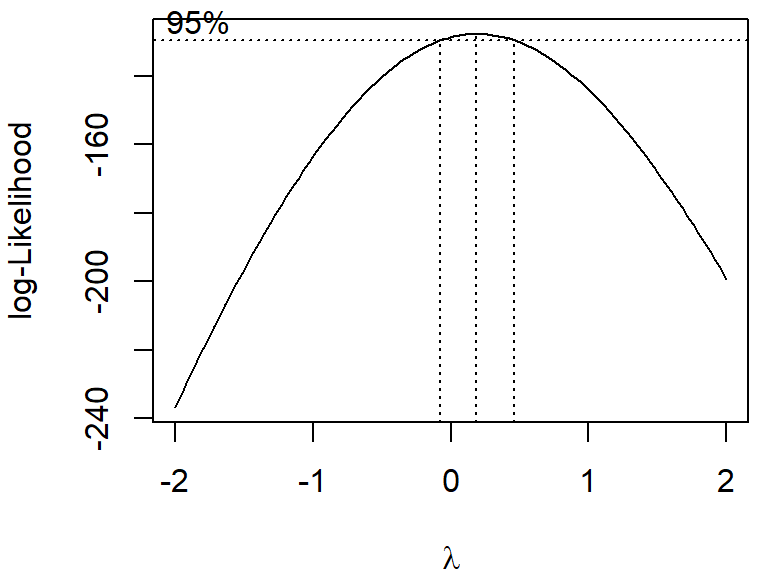
boxcox is a “model formula” or the outcome of a linear model (lm)~ 1).biovol ~ groupFrequencies of nominal variables
⇒ dependence between plant society and soil type
(see before)
Ordinal variables
\(\rightarrow\) rank numbers
Metric scales
Variance
\[ s^2_x = \frac{\text{sum of squares}}{\text{degrees of freedom}}=\frac{\sum_{i=1}^n (x_i-\bar{x})^2}{n-1} \]
Covariance
\[ q_{x,y} = \frac{\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})}{n-1} \]
Correlation: scaled to \((-1, +1)\)
\[ r_{x,y} = \frac{q_{x,y}}{s_x \cdot s_y} \]
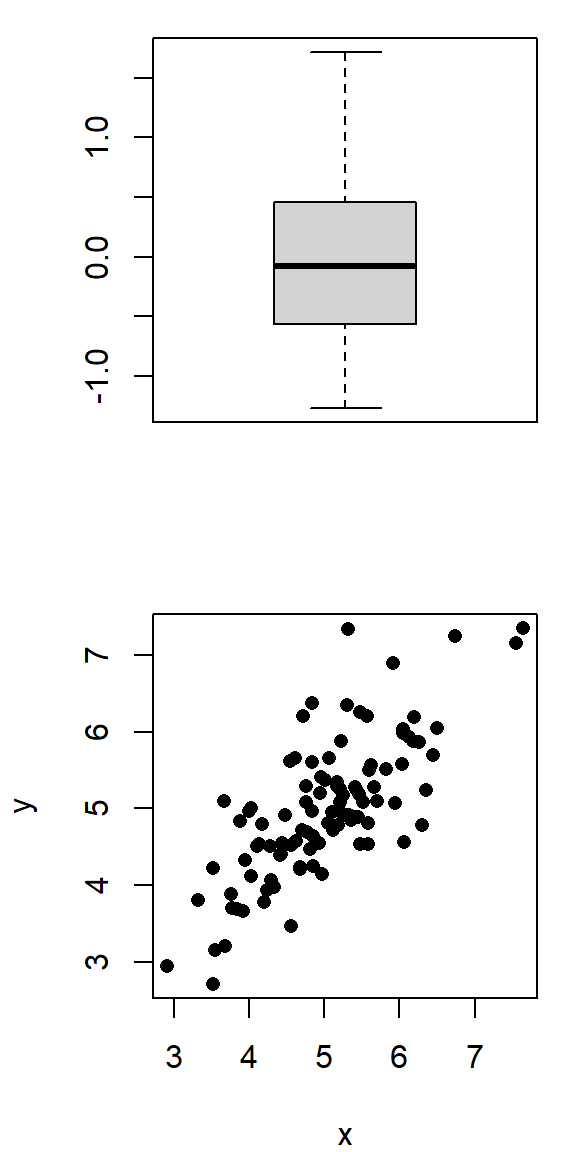
\[ r_p=\frac{\sum{(x_i-\bar{x}) (y_i-\bar{y})}} {\sqrt{\sum(x_i-\bar{x})^2\sum(y_i-\bar{y})^2}} \]
Or:
\[
r_p=\frac {\sum xy - \sum y \sum y / n}
{\sqrt{(\sum x^2-(\sum x)^2/n)(\sum y^2-(\sum y)^2/n)}}
\]
Range of values: \(-1 \le r_p \le +1\)
| \(0\) | no interdependence |
| \(+1 \,\text{or}\,-1\) | strictly positive resp. negative dependence |
| \(0 < |r_p| < 1\) | positive resp. negative dependence |
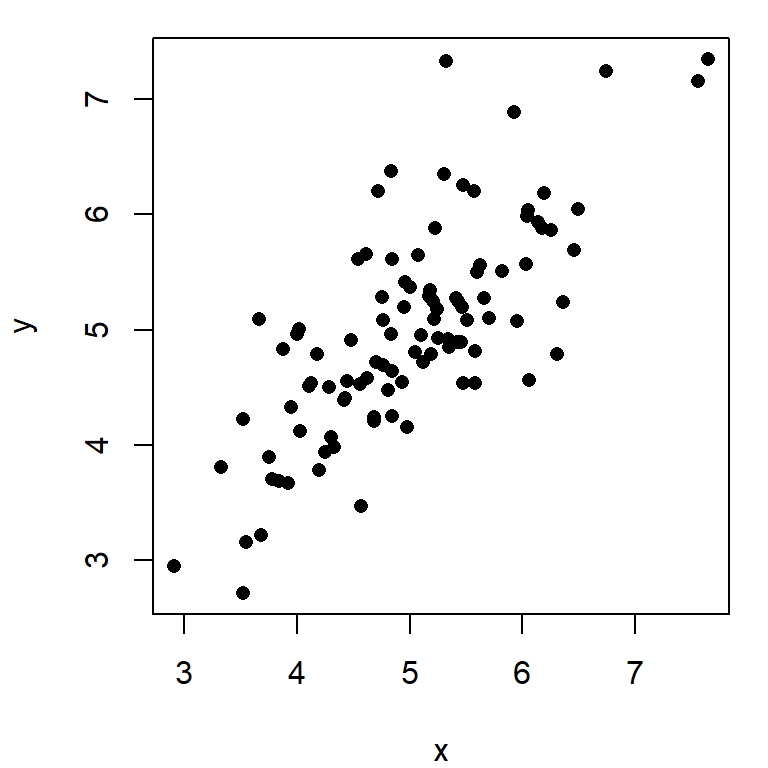
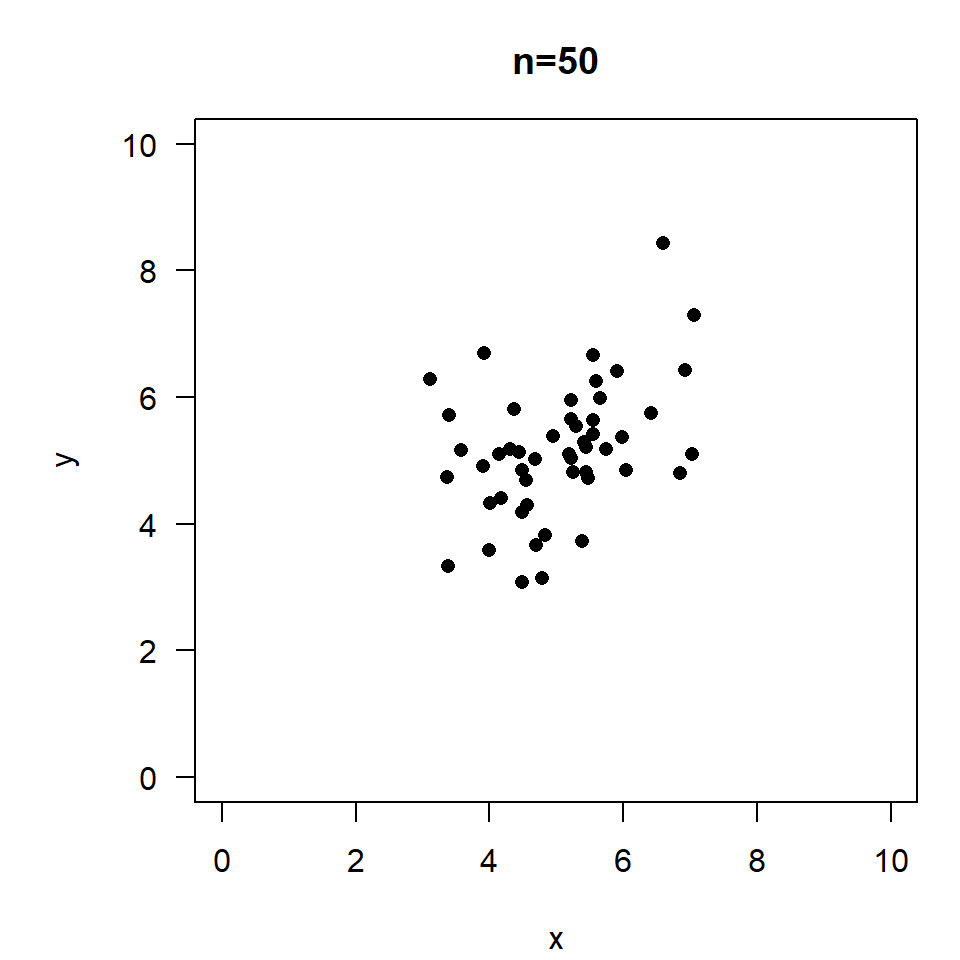
\(r=0.4, \quad p=0.0039\)
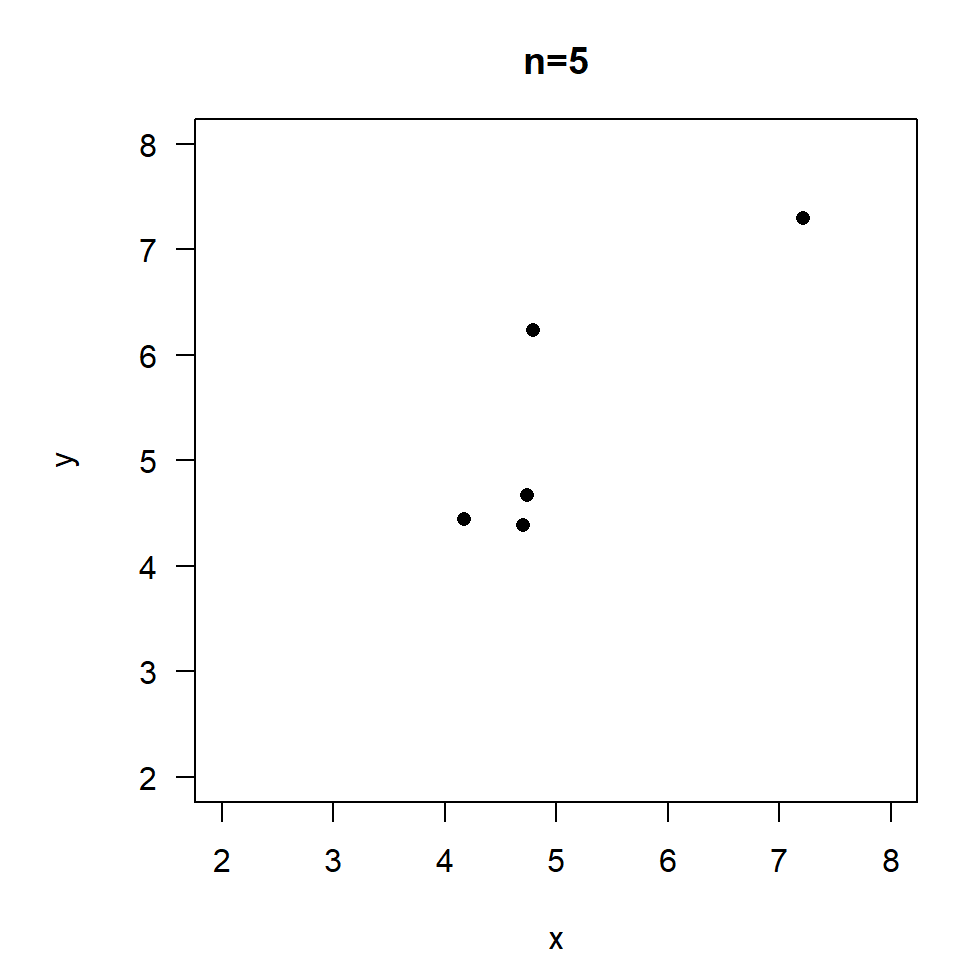
\(r=0.85, \quad p=0.07\)
\[ \hat{t}_{\alpha/2;n-2} =\frac{|r_p|\sqrt{n-2}}{\sqrt{1-r^2_p}} \]
\(t=0.829 \cdot \sqrt{1000-2}/\sqrt{1-0.829^2}=46.86, df=998\)
Quick test: critical values for \(r_p\)
| \(n\) | d.f. | \(t\) | \(r_{crit}\) |
| 3 | 1 | 12.706 | 0.997 |
| 5 | 3 | 3.182 | 0.878 |
| 10 | 8 | 2.306 | 0.633 |
| 20 | 18 | 2.101 | 0.445 |
| 50 | 48 | 2.011 | 0.280 |
| 100 | 98 | 1.984 | 0.197 |
| 1000 | 998 | 1.962 | 0.062 |
\[ r_s=1-\frac{6 \sum d^2_i}{n(n^2-1)} \]
for \(10 \leq n\) \(\rightarrow\) \(t\)-distribution
\[ \hat{t}_{1-\frac{\alpha}{2};n-2} =\frac{|r_s|}{\sqrt{1-r^2_S}} \sqrt{n-2} \]
| \(x\) | \(y\) | \(R_x\) | \(R_y\) | \(d\) | \(d^2\) |
|---|---|---|---|---|---|
| 1 | 2.7 | 1 | 1 | 0 | 0 |
| 2 | 7.4 | 2 | 2 | 0 | 0 |
| 3 | 20.1 | 3 | 3 | 0 | 0 |
| 4 | 500.0 | 4 | 5 | -1 | 1 |
| 5 | 148.4 | 5 | 4 | +1 | 1 |
| 2 | |||||
\[ r_s=1-\frac{6 \cdot 2}{5\cdot (25-1)}=1-\frac{12}{120}=0.9 \]
For comparison: \(r_p=0.58\)
Advantages
Disadvantages:
Conclusion: \(r_s\) is nevertheless highly recommended!
Pearson's product-moment correlation
data: x and y
t = 7.969, df = 4, p-value = 0.001344
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.7439930 0.9968284
sample estimates:
cor
0.9699203 If linearity or normality of residuals is doubtful, use a rank correlation
Multiple correlation
Recommendation: