03-Statistical Parameters

Applied Statistics – A Practical Course

Thomas Petzoldt

2025-09-16

Statistical Parameters


\(\rightarrow\) Remember: calculation of statistical parameters is called estimation

Properties of statistical parameters

  • Unbiasedness: the estimation converges towards the true value with increasing \(n\)
  • Efficiency a relatively small \(n\) is sufficient for a good estimation
  • Robustness the estimation is not much influenced by outliers or certain violations of statistical assumptions

Depending on a particular question, different classes of parameters exist, especially measures of location (e.g. mean, median), variation (e.g. variance, standard deviation) or dependence (e.g. correlation).

Measures of location I

Arithmetic mean

\[ \bar{x} = \frac{1}{n} \cdot {\sum_{i=1}^n x_i} \]

Geometric mean

\[ G = \sqrt[n]{\prod_{i=1}^n x_i} \]

more practical: logarithmic form:

\[ G =\exp\Bigg(\frac{1}{n} \cdot {\sum_{i=1}^n \ln{x_i}}\Bigg) \]

avoids huge numbers that make problems for the computer.

Measures of location II

Harmonic mean

\[ \frac{1}{H}=\frac{1}{n}\cdot \sum_{i=1}^n \frac{1}{x_i} \quad; x_i>0 \]

Example:

You drive with 50km/h to the university and with 100km/h back home.
What is the mean velocity?

Result:

1/((1/50 + 1/100)/2) = 1/((0.02 + 0.01)/2) = 1/0.015 = 66.67

Median (central value)


\(n\) uneven: sort data, take the middle value

\[\tilde{x} = x_{(n+1)/2}\] \(n\) even: sort data, take average of the two middle values

\[\tilde{x} = \frac{x_{n/2}+x_{n/2+1}}{2}\]

Example

sample with 7 values 2.9, 7.9, 4.1, 8.8, 9.4, 0.5, 5.3
ordered sample 0.5, 2.9, 4.1, 5.3, 7.9, 8.8, 9.4

\(\Rightarrow\) median: \(\tilde{x} = 5.3\)

\(\Rightarrow\) mean: \(\bar{x} = 5.5571429\)

Trimmed mean


  • also called “truncated mean”
  • compromize between the arithmetic mean and median
  • A certain percentage of smallest and biggest values is ignored (e.g. 10% or 25%) before calculating the arithmetic mean
  • used also in sports

Example: sample with 20 values, exclude 10% at both sides

0.4, 0.5, 1, 2.5, 2.9, 3.3, 4.1, 4.5, 4.6, 5.3, 5.5, 5.7, 6.8, 7.9, 8.8, 8.9, 9, 9.4, 9.6, 46

\(\rightarrow\) arithmetic mean: \(\bar{x}=7.335\)
\(\rightarrow\) trimmed mean: \(\bar{x}_{t, 0.1}=5.6375\)

  • median and trimmed mean are less influenced by outliers and skewnes \(\rightarrow\) more robust
  • but somewhat less efficient

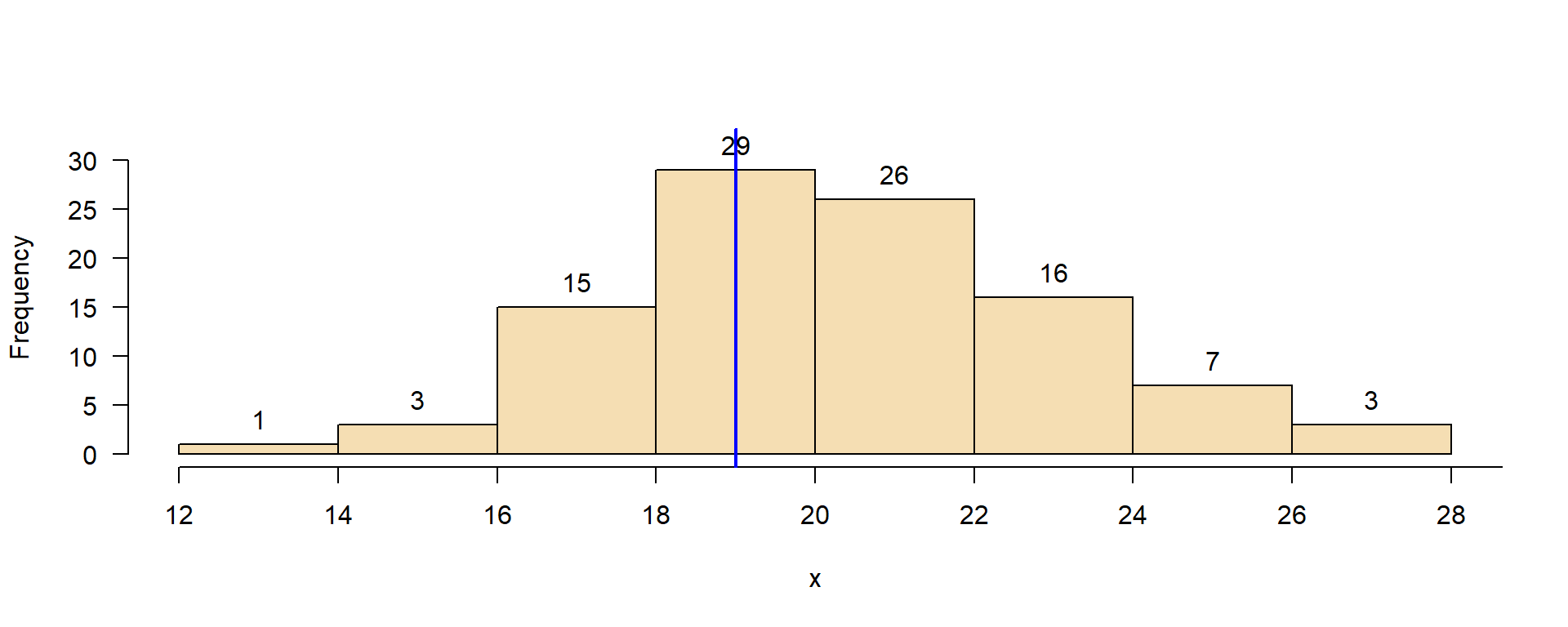
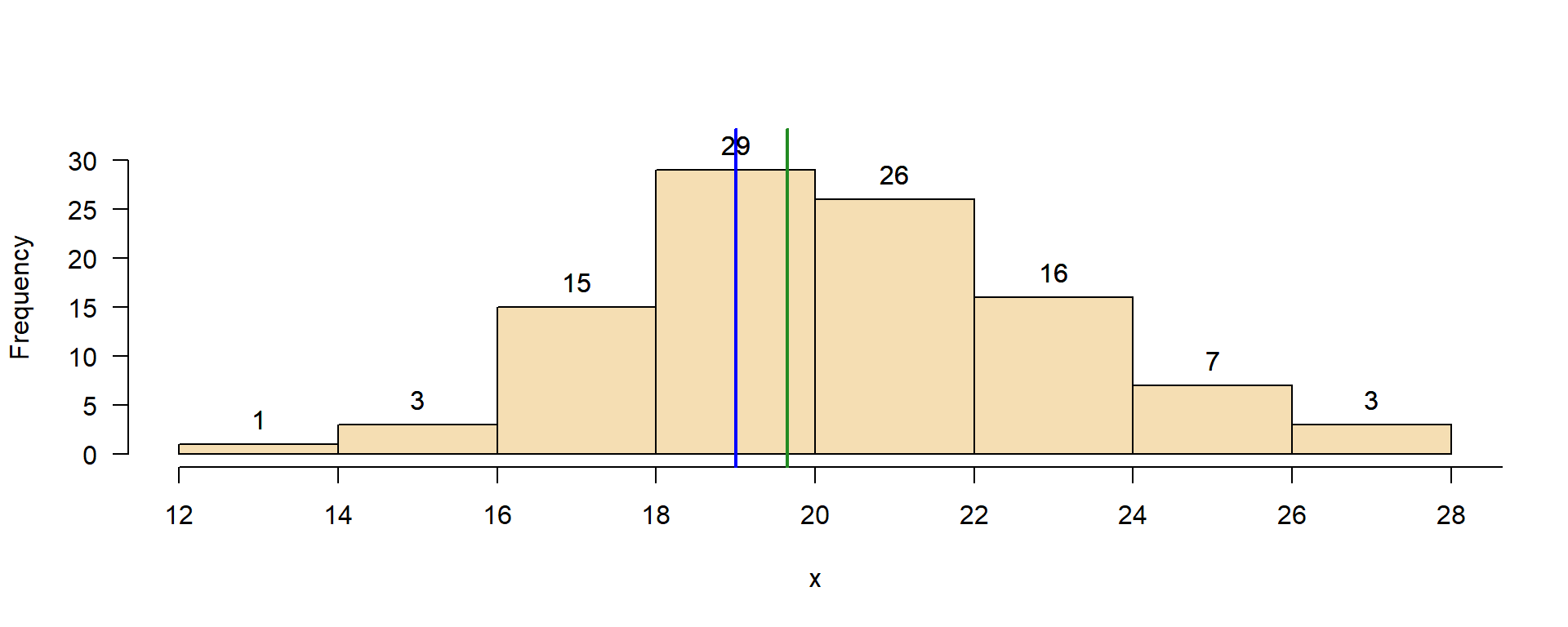
Mode (modal value)

  • most frequent value of a sample
  • strict definition only valid for discrete (binary, nominal, ordinal) scales
  • extension to continuous scale: binning or density estimation

First guess: middle of most-frequent class.

Mode: weighting formula

\[\begin{align} D &= x_{lo}+\frac{f_k-f_{k-1}}{2f_k-f_{k-1}-f_{k+1}}\cdot w \\ D &= 18 + \frac{29 - 15}{2 \cdot 29 - 15 - 26} \cdot 2 = 19.65 \end{align}\]

\(f\): class frequency, \(w\): class width

\(k\): the index of the most abundant class, \(x_{lo}\) its lower limit.

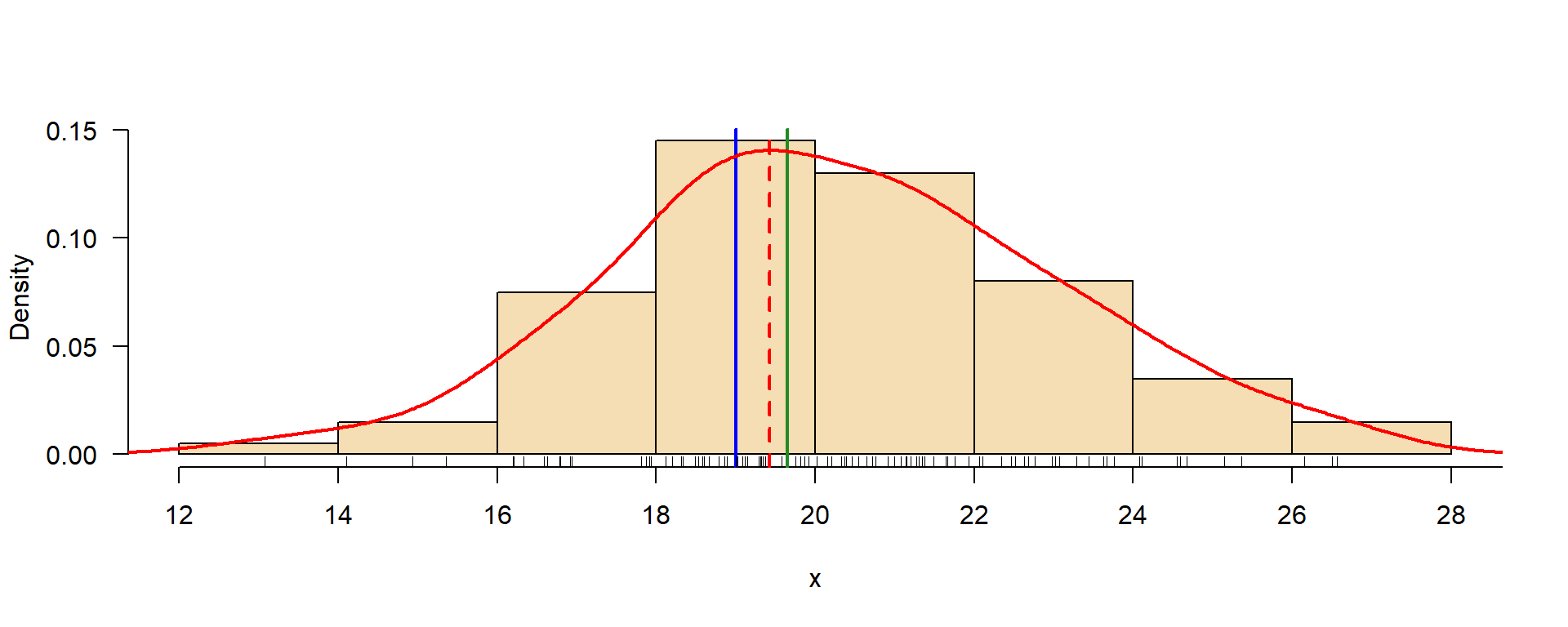
Mode: density estimation

Somewhat more computer intensive, where the mode is the maximum of a kernel density estimate.

The mode from the density estimate is then \(D=19.42\).

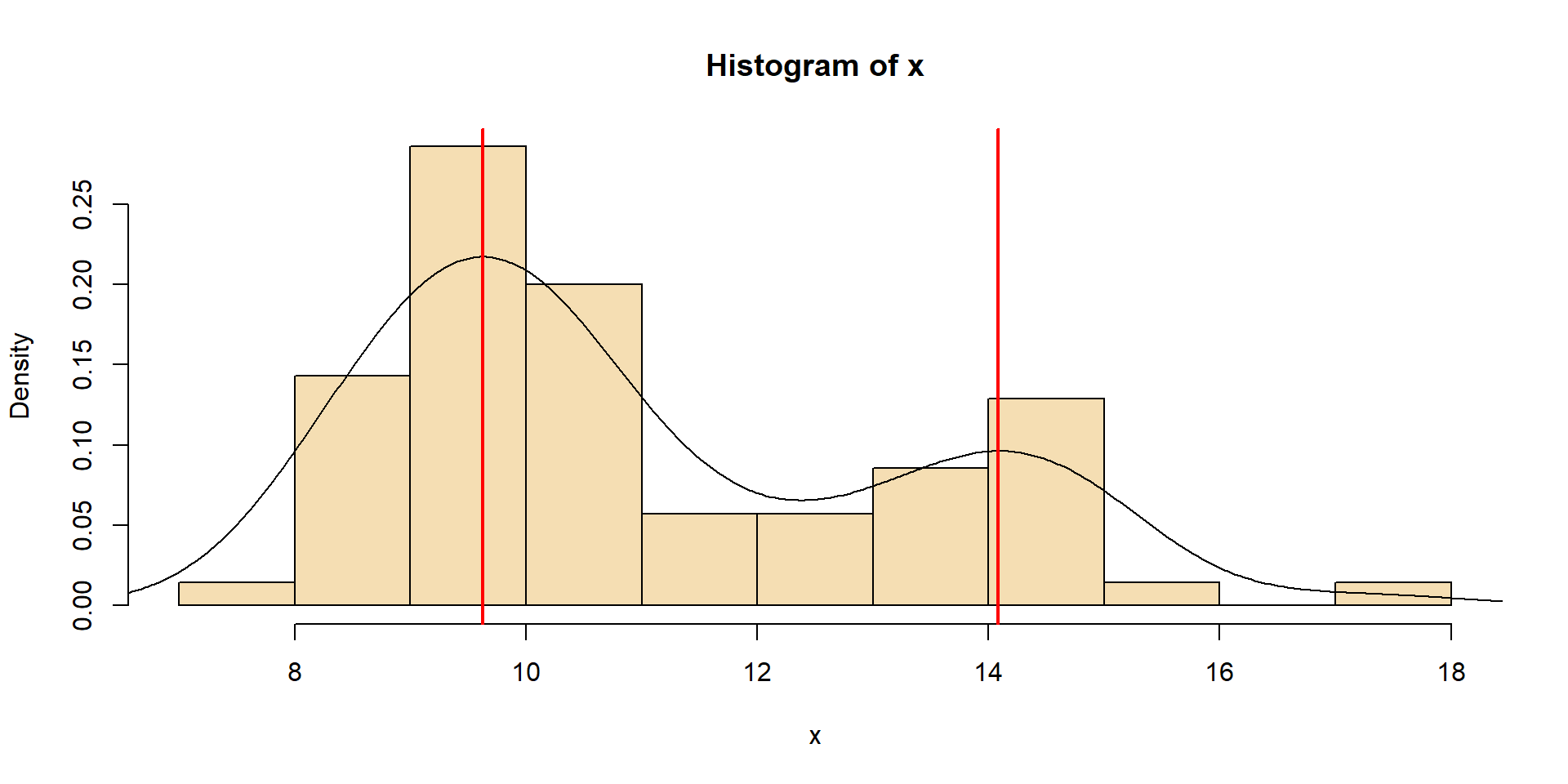
Multi-modal distribution

Example: fish population with several age classes, cohorts)

Measures of variation

Variance

\[ s^2_x = \frac{SQ}{df}=\frac{\sum_{i=1}^n (x_i-\bar{x})^2}{n-1} \]

  • \(SQ\): sum of squared differences from the mean \(\bar{x}\)
  • \(df = n-1\): degrees of freedom, \(n\): sample size

Standard deviation

\[s=\sqrt{s^2}\] \(\rightarrow\) same unit as the mean \(\bar{x}\), so they can be directly compared.

In practice, \(s^2\) is often computed with:

\[ s^2_x = \frac{\sum{(x_i)^2}-(\sum{x_i})^2/n}{n-1} \]

Coefficient of variation (\(cv\))

Is the relative standard deviation:

\[ cv=\frac{s}{\bar{x}} \]

  • useful to compare variations of different variables, independent of their measurement unit
  • only applicable for data with ratio scale, i.e. with an absolute zero (like meters)
  • not for variables like Celsius temperature or pH.

Example

Let’s assume we have the discharge of two rivers, one with a \(cv=0.3\), another one with \(cv=0.8\). We see that the 2nd has more extreme variation.

Range


The range measures the difference between maximum and minimum of a sample:

\[ r_x = x_{max}-x_{min} \]


Disadvantage: very sensitive against outliers.

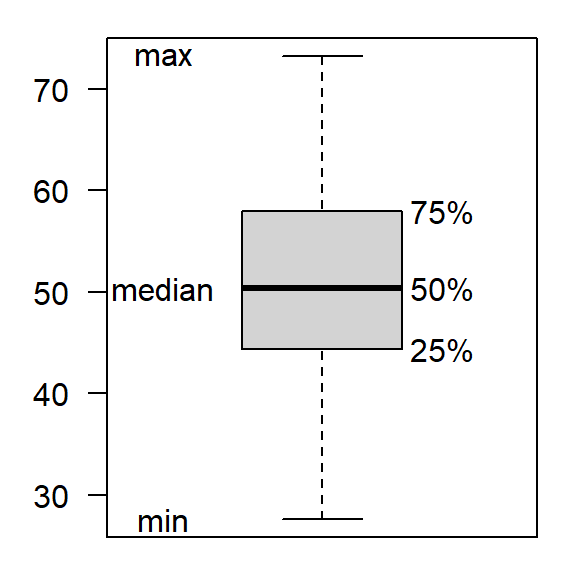
Interquartile range

  • IQR or \(I_{50}\) omits smallest and biggest 25%
  • sample size of at least 12 values recommended

\[ I_{50}=Q_3-Q_1=P_{75}-P_{25} \]

Ordered sample

  • \(Q_1\), \(Q_3\): 1st and 3rd quartiles
  • \(P_{25}, P_{75}\): 25th and 75th percentile
  • typically used in boxplots

For normally distributed samples, fixed relationship between \(I_{50}\) and \(s\):

\[ \sigma = E(I_{50}/(2\Phi^{-1}(3/4))) \approx E(I_{50}/1.394) % 2*qnorm(3/4)) \]

where \(\Phi^{-1}\) is the quantile function of the normal distribution.

Median absolute deviation


The median of the absolute differences between median and values.

\[ MAD = \text{median}(|\text{median} - x_i|) \]

  • frequently used in some communities, rarely used in our field
  • some programs rescale the MAD with a factor \(1.4826\) to approximate the standard deviation.

\(\rightarrow\) Be careful and check the software docs!

Standard error of the mean

\[ s_{\bar{x}}=\frac{s}{\sqrt{n}} \]

  • measures the accuracy of the mean
  • plays a central role for calculation of confidence intervals and statistical tests

Rule of thumb for a sample size of about \(n > 30\):

  • “Two sigma rule”: the true mean is with 95% in the range of \(\bar{x} \pm 2 s_\bar{x}\)

Important


  • standard deviation \(s\) measures variability of the sample
  • standard error \(s_\bar{x}\) measures accuracy of the mean

More about this will be explained in the next sections.