09-Generalized Linear Models

Angewandte Statistik – Ein Praxiskurs

Thomas Petzoldt

2025-12-13

Ausgewählte Beispiele

Was ist ein Generalisiertes Lineares Modell (GLM)?

Erweitert die Theorie der linearen Modelle auf bestimmte nichtnormalverteilte Responsevariablen durch die Verwendung einer Link-Funktion.

Poisson-Verteilung:
- Zähldaten, z.B. Vorkommen von Tieren.
- Häufigkeit von Ereignissen: \(0, 1, 2, 3, \dots\) Zahlen sind strikt positiv, Null kann vorkommen.
Binomial-Verteilung:
- Binäre Variablen (lebend/tot, vorhanden/nicht vorhanden) oder Dosis-Wirkungsbeziehungen.
- Nominelle Variablen (Faktorstufen) mit zwei oder mehr Ausprägungen.
Gamma-Verteilung:
- Metrische Variablen, oft rechtsschief (z. B. Reaktionszeiten, Wartezeiten).
- Vermeidet Transformationen (z.B. log-Transformation) der Responsevariable.

Verteilungsfamilie und Linkfunktion

Ein GLM trennt das Modells in drei Komponenten:

1. Zufallskomponente (Verteilungsfamilie):
- Definiert die Wahrscheinlichkeitsverteilung der Responsevariable \(Y\).
- Legt fest, welche Verteilung die Daten (z. B. Poisson, Binomial, Gamma) annehmen.
2. Systematische Komponente (Linearer Prädiktor):
- Die bekannte lineare Gleichung: \(\eta = \beta_0 + \beta_1 X_1 + \dots\)
- Enthält alle Kovariablen und deren Koeffizienten.
3. Linkfunktion:
- Verbindet die Zufallskomponente (den Erwartungswert \(E(Y)\) des Response) mit der Systematischen Komponente (dem linearen Prädiktor \(\eta\)).
- Transformation des Erwartungswertes: \(g(E(Y)) = \eta\)

Beispiel: Bei binären Daten transformiert die Logit-Linkfunktion die Wahrscheinlichkeiten (die zwischen 0 und 1 liegen müssen) auf die gesamte reelle y-Achse (\(-\infty\) bis \(+\infty\)), damit sie mit dem linearen Modell übereinstimmen.

Typische Familien und Kanonische Linkfunktionen

Die Wahl der Linkfunktion hängt von der Verteilung der Response ab.

Kanonische Linkfunktion: ist die Standard- und rechnerisch effizienteste Wahl.

Verteilungsfamilie	Response-Typ	Kanonische Linkfunktion	Funktion
Normal (Gauß)	Metrisch, kontinuierlich	Identitäts-Link	\(g(\mu) = \mu\)
Poisson	Zähldaten (Counts)	Log-Link	\(g(\mu) = \log(\mu)\)
Binomial	Binär (0/1), Proportionen	Logit-Link	\(g(\mu) = \log(\frac{\mu}{1-\mu})\)
Gamma	Metrisch, positiv, schief	Reziprok-Link	\(g(\mu) = 1/\mu\)
Inverse Gauß	Metrisch, positiv, schief	Reziprok-Quadrat-Link	\(g(\mu) = 1/\mu^2\)

Flexible Anpassungen möglich

Quasi-Poisson / Quasi-Binomial:
- Wird verwendet, wenn eine Über- oder Unterdispersion vorliegt. – Varianz ist größer oder kleiner als von Poisson oder Binomial angenommen.
Nicht-kanonische Linkfunktionen:
- Für bestimmte Interpretation oder Datentypen.
- Bei der Binomialverteilung kann statt des Logit-Links der Probit-Link (basiert auf der Normalverteilung) verwendet werden.

Modellformel

Sieht im Prinzip genauso aus, wie bei lm:

glm(growth ~ pH + nutrient, data = growthdata, family = binomial)

Beispiel: Binomialverteilung

Modellierung von Wahrscheinlichkeiten eines Ereignisses.
Definitiv viel besser als Arbeiten mit Prozentzahlen!

Responsevariable

Die Responsevariable enthält entweder einen langen Vektor mit (0, 1) für die Ereignisse oder eine Matrix mit zwei Spalten mit den Häufigkeiten für “ja” oder “nein”.

Erklärungsvariablen

Standard: Die Wahrscheinlichkeit steigt monoton mit dem Prädiktor (z. B. Dosis).
Optimum: Die Wahrscheinlichkeit steigt zuerst an und fällt dann wieder ab, z. B. Wachstum in Abhängigkeit vom pH. Quadratischer Term in der Modellformel: I(x^2)

glm(growth ~ pH + I(pH^2), data = growthdata, family = binomial)

Durch die Funktion I() (AsIs) wird der Term arithmetisch und nicht symbolisch interpretiert.

GLM Datenstruktur im R-Code

Die Binomial-Familie akzeptiert zwei primäre Formate für die Responsevariable:

A: Logischer Vektor (0/1)

Jede Zeile repräsentiert einen einzelnen Versuch.

df_vektor <- data.frame(
  pH = c(5.0, 5.2, 5.5, 5.8, 6.0, 6.2, 6.5, 6.7, 7.0, 7.2),
  # 1 = Gekeimt (Erfolg), 0 = Nicht Gekeimt (Misserfolg)
  keimung = c(0, 0, 1, 1, 1, 1, 1, 0, 0, 0)
)

# Modellaufruf:
# glm(keimung ~ pH + I(pH^2), data = df_vektor, family = binomial)

B: Häufigkeits-Matrix

Jede Zeile repräsentiert die Replikate mit aggregierten Zählungen.

df_matrix <- data.frame(
  pH = c(5.0, 5.5, 6.0, 6.5, 7.0),
  Anzahl_gesamt = c(20, 20, 20, 20, 20),
  # Spalten müssen "Erfolge" und "Misserfolge" sein
  Erfolg = c(2, 8, 18, 12, 3), 
  Misserfolg = c(18, 12, 2, 8, 17) # Anzahl_Samen - Erfolg
)

# Modellaufruf:
# glm(cbind(Erfolg, Misserfolg) ~ pH, data = df_matrix, family = binomial)

Wichtig beim Matrix-Format:

Der Response muss mit cbind(Erfolg, Misserfolg) im Modellaufruf angegeben werden.
Dieses Format ist effizienter bei großen, aggregierten Datensätzen.

Anwendung: Toxizitätstest (Toxtest)

Ziel: Modellierung der Mortalität als Funktion der Dosis.

Datenstruktur (7 Dosisstufen): Verwendung des Matrix-Formats.

library(dplyr)

daphnia <- data.frame(
  number   = c(11, 13, 17, 10, 11, 10, 11), 
  dose     = c(1,  2,  4,  8, 16, 32, 64),
  dose_log = c(0, 1, 2, 3, 4, 5, 6),        # zur Vereinfachung log_2 transformiert
  survived = c(11, 12, 17, 6, 2, 0, 0)
)

plot(survived/(number) ~ dose, data = daphnia, pch=16)

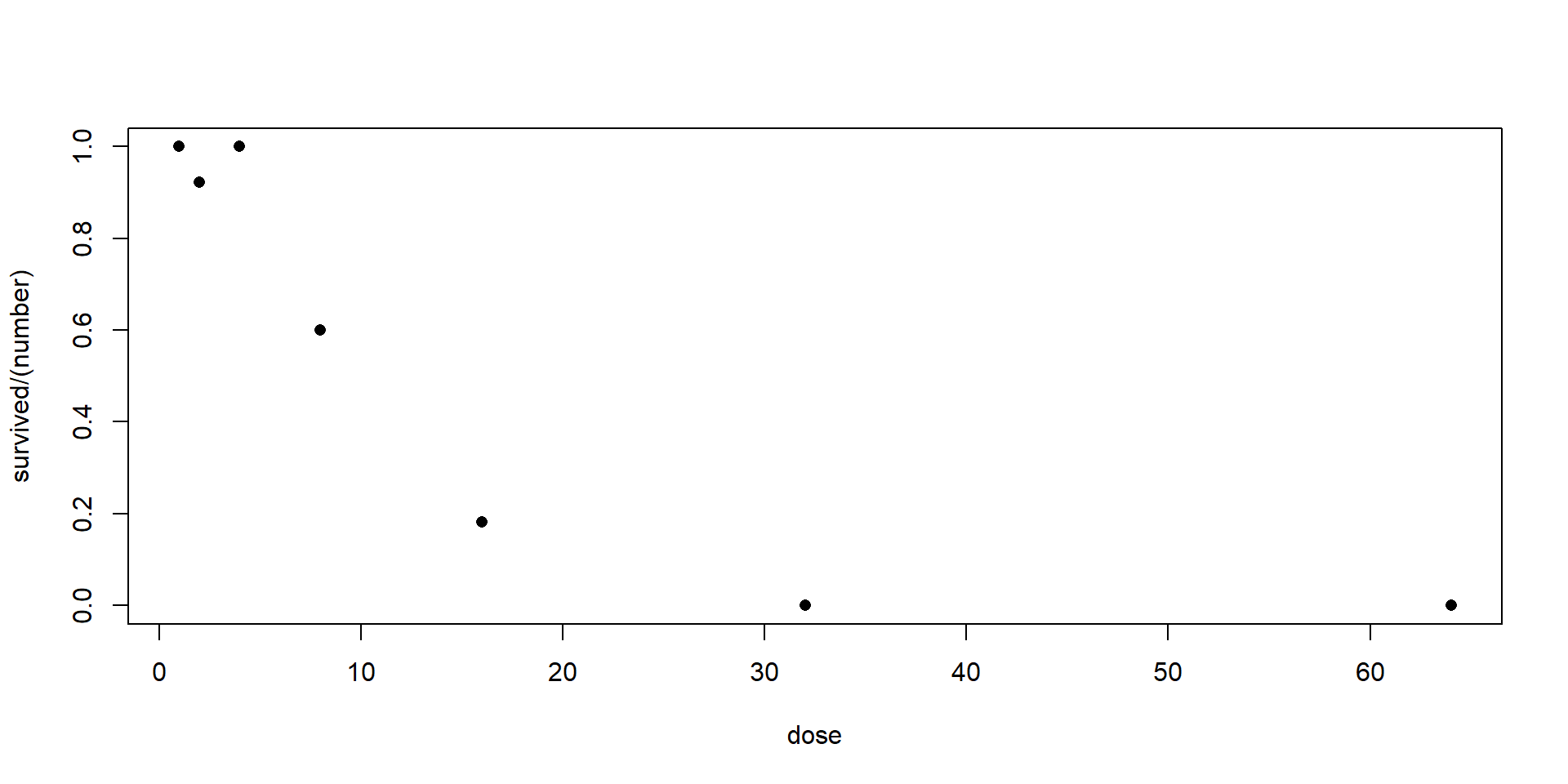
Fitten des Modells und statistischer Test

# Vorbereitung für 2spaltige Datenstruktur cbind(Erfolg, Misserfolg)
daphnia <- daphnia |> mutate(dead = number - survived)

## Fitten des GLM
m <- glm(cbind(survived, dead) ~ dose_log, data = daphnia, family = binomial(link = "logit"))

# Test der Gesamtsignifikanz (Äquivalent zur F-Statistik im lm)
anova(m, test="Chi")

Analysis of Deviance Table

Model: binomial, link: logit

Response: cbind(survived, dead)

Terms added sequentially (first to last)

         Df Deviance Resid. Df Resid. Dev  Pr(>Chi)    
NULL                         6     82.076              
dose_log  1   76.444         5      5.632 < 2.2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Response: cbind(survived, dead) (Überleben, Tod).
Test: Der Chi-Quadrat-Test aus der ANOVA zeigt, ob das Modell mit dose_log besser ist als ein Nullmodell.

Visualisierung

Transformation der Vorhersage von der Link-Skala zurück zur Wahrscheinlichkeits-Skala

# Predict on the 'link' scale to get standard errors
dose_seq <- data.frame(dose_log = seq(0, 6, length.out = 100))
preds    <- predict(m, newdata = dose_seq, type = "link", se.fit = TRUE)

# Calculate CI on the link scale and back-transform
fit_link <- preds$fit
se_link  <- preds$se.fit

dose_seq$prob <- plogis(fit_link)
dose_seq$lwr  <- plogis(fit_link + (qnorm(0.025) * se_link))
dose_seq$upr  <- plogis(fit_link + (qnorm(0.975) * se_link))

Interpretation:

Link-Skala: Log-Odds, Werte von \(-\infty\) bis \(+\infty\).
Response-Skala: Wahrscheinlichkeiten, Werte von \(0\) bis \(1\).
plogis() ist die Umkehrfunktion (Inverse) des Logit-Links.

Konfidenzintervalle

Code

plot(daphnia$dose_log, daphnia$survived / daphnia$number,
     pch = 16, col = "darkblue", ylim = c(0, 1), las=1,
     xlab = "log2(Dose)", ylab = "Proportion Survived (p)")
lines(dose_seq$dose, dose_seq$prob, lwd = 2, col = "red")

lines(dose_seq$dose_log, dose_seq$upr, lty="dashed")
lines(dose_seq$dose_log, dose_seq$lwr, lty="dashed")
abline(h=0.5, lty="dotted")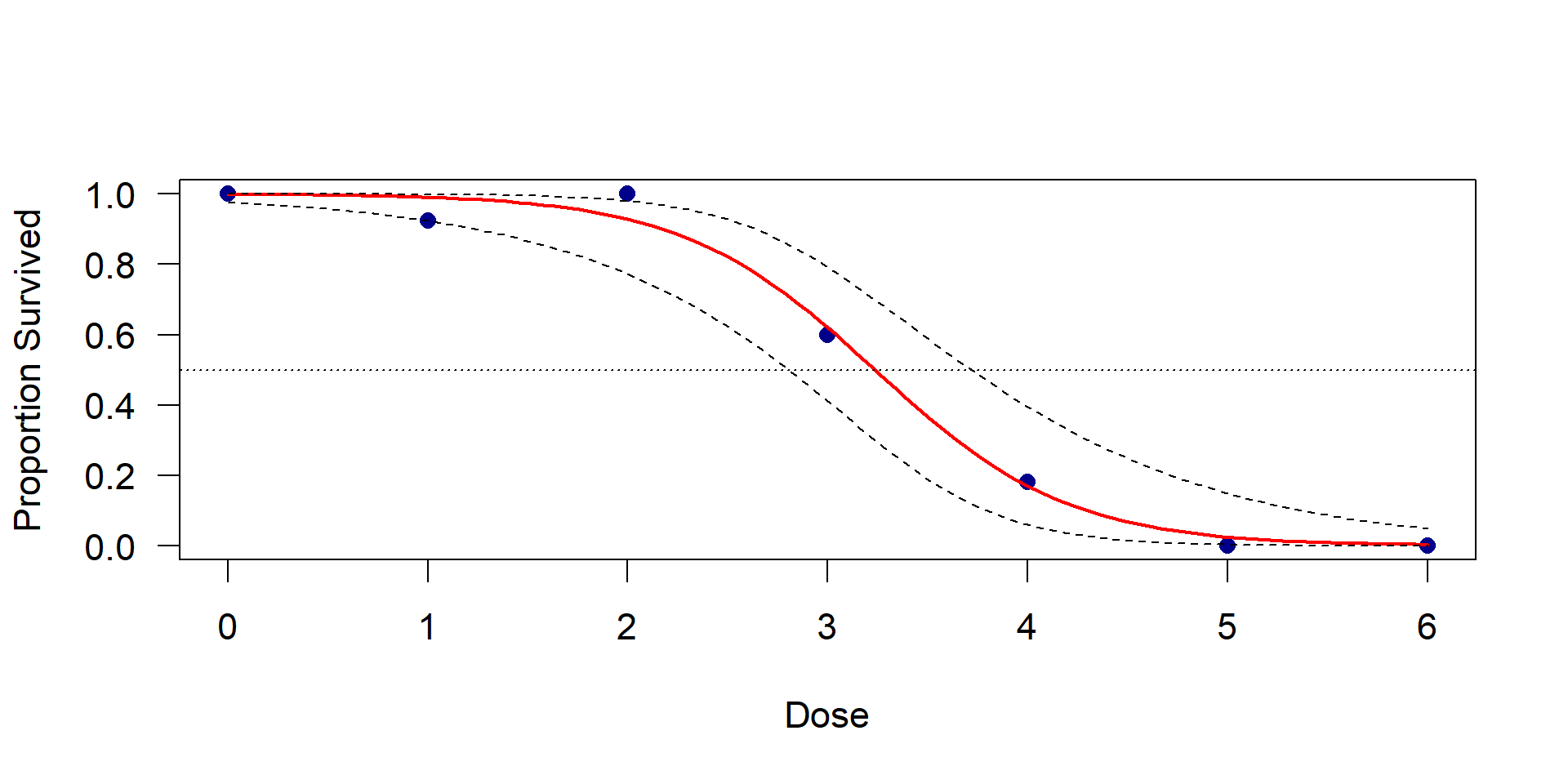

Wir verwenden den \(z\)-Wert (qnorm), da in GLMs die Normalverteilung der Koeffizienten (asymptotische Theorie) angenommen wird.
plogis() ist die Umkehrfunktion des Logit-Links.
Rot: Die vom Modell geschätzte Überlebenswahrscheinlichkeit.
Gestrichelt: Das 95%-Konfidenzintervall.
Gepunktet (EC50): Schnittpunkt der Kurve mit \(\text{p}=0.5\). An diesem Punkt ist der lineare Prädiktor \(\eta\) genau Null.

Numerische Schätzung der EC50

EC50 Konzentration, bei der 50% der Organismen überleben, p=0.5
linearer Prädiktor \(\eta\) ist Null)
Schätzung des Konfidenzintervalls mittels Delta-Methode

\[ \text{LC}_{50} = -\beta_{\text{Intercept}} / \beta_{\text{Dose}} \]

# Koeffizienten und Varkov-Matrix abrufen
b <- coef(m); V <- vcov(m)

b0 <- b["(Intercept)"]  # b0
b1 <- b["dose_log"]     # b1

EC50, Standardfehler und CI

\(LC_{50} = - b_0 / b_1\)
Berechnung des Standardfehlers (\(\text{se}\)) mit der Delta-Methode:

se <- sqrt(V[1,1]/b1^2 + V[2, 2] * b0^2 / b1^4 - 2*V[1,2] * b0/b1^3)

# 95%-Konfidenzintervall
ec50 <- -b0 / b1
CI <- ec50 + qnorm(c(0.025, 0.975)) * se
cat("ec50 =", ec50, "CI = (", CI, ")\n")

ec50 = 3.235783 CI = ( 2.828378 3.643188 )

GLM Diagnostik: Residuen und Leverage

Die Modellannahmen müssen überprüft werden, um die Zuverlässigkeit der Ergebnisse sicherzustellen.

Unabhängigkeit: Beobachtungen (z.B. Daphnien) sind voneinander unabhängig.
Korrekte Spezifikation: Der Zusammenhang (hier: logistisch) ist korrekt spezifiziert.
Keine Überdispersion: Die beobachtete Variabilität entspricht der theoretischen Variabilität der gewählten Familie (Binomial).

Diagnostik-Plots

Im GLM überprüfen wir standardmäßig vier Haupt-Plots:

Deviance Residuen vs. Fitted Values
Normal Q-Q Plot: Normalverteilung der Residuen
Scale-Location Plot: Überprüft die Homoskedastizität
Hebelwirkung (Leverage)
- Leverage: Punkte mit ungewöhnlichen Prädiktorwerten (z.B. sehr hohe Dosis).
- Cook’s Distance: Einfluss jedes Datenpunkts auf die Modellschätzung.

Diagnostik-Plots

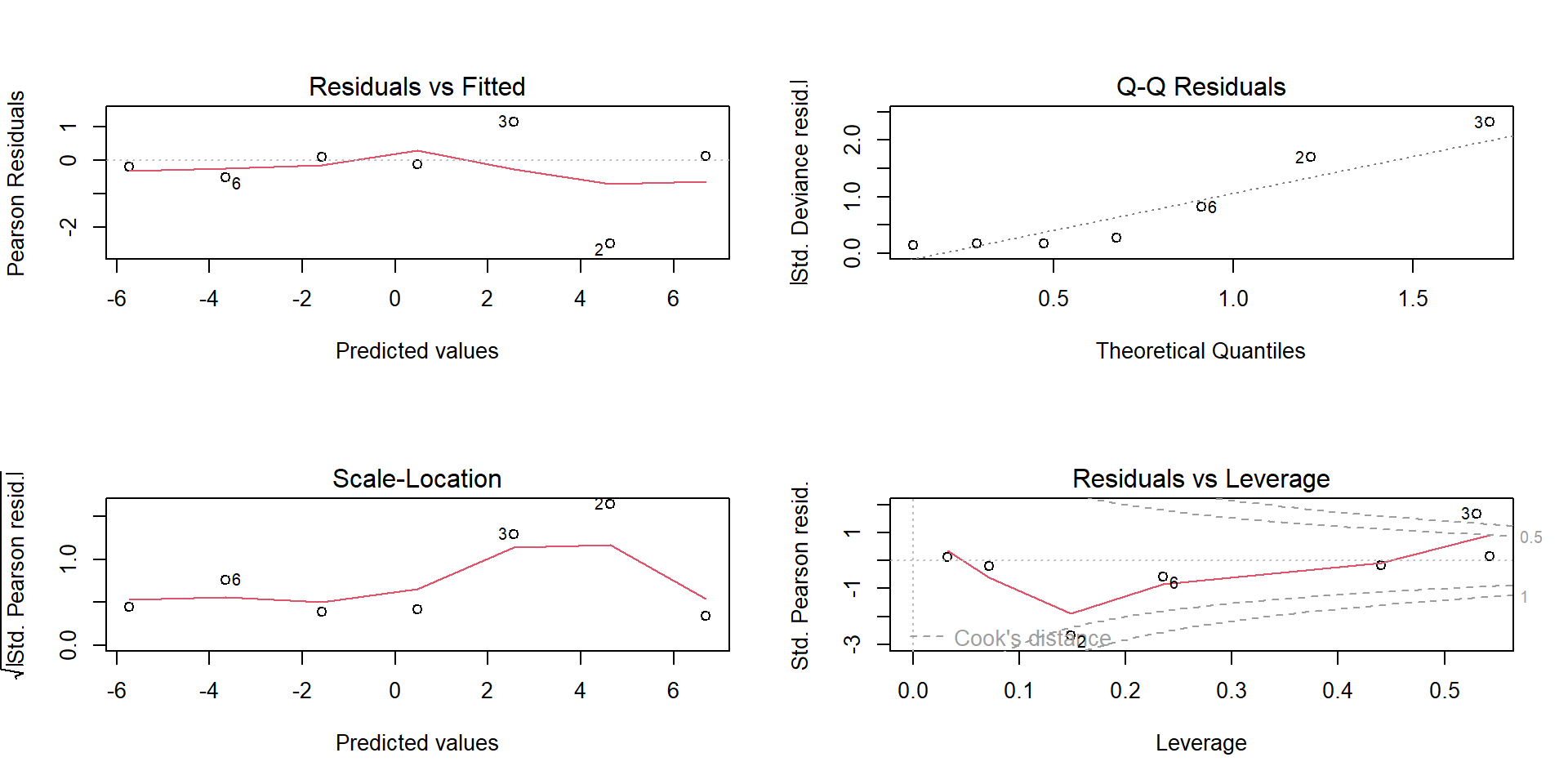
Diagnostik: Einfluss und Residuen

Überprüfung der Modellannahmen nach dem Fitten.

A: Einflussreiche Punkte (Leverage)

Plot: Cook’s Distance und Leverage.
Interpretation: Üben die Beobachtungen einen gleichmäßigen und geringen Einfluss aus (\(\approx 1/n\))?
Sind extreme Ausreißer vorhanden, die das Modell verzerren?

B: Residuen-Analyse

Plot: Q-Q-Plot der deviance-Residuen.
Interpretation: Ist die Verteilung schief oder hat sie “schwerere Tails” als eine reine Normalverteilung?
GLMs sind robust gegenüber leichten Abweichungen der Residuen-Normalität.

Dosis-Wirkungs-Analyse mit drc

Analyse des Toxtests mit dem drc-Paket

Das \(\text{drc}\)-Paket (Ritz et al., 2015) enthält Funktionen speziell für die Dosis-Wirkungs-Analyse.
Daten nicht im \(\text{cbind}\)-Format, sondern Verhältnis (events/trials) und Gesamtzahl (weights).
Falls die Dosis im logarithmiert vorliegt, muss die Basis angegeben werden (logDose).

library(drc)
# Fitten eines Log-Logistischen Modells
m_drc <- drm(survived / number ~ dose_log, weights = number, 
             data = daphnia, type = "binomial",
             fct = LL.3(), logDose = 2)
summary(m_drc)


Model fitted: Log-logistic (ED50 as parameter) with lower limit at 0 (3 parms)

Parameter estimates:

              Estimate Std. Error t-value   p-value    
b:(Intercept) 3.972751   1.145539  3.4680 0.0005243 ***
d:(Intercept) 0.975727   0.025955 37.5927 < 2.2e-16 ***
e:(Intercept) 9.995332   1.347866  7.4157  1.21e-13 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Das 3-Parameter-Modell (LL.3) ist oft eine robustere Alternative zum einfachen \(\text{GLM}\).

Plot und ED₅₀ bzw. EC₅₀

**drc*+ vereinfacht Visualisierung und Schätzung der EC₅₀.

Plot mit 95% CI

plot(m_drc, type = "all", xlab = "Log2-Dosis")

Schätzung der EC50 (ED50) mit CI

ED(m_drc, respLev = 50, interval = "delta")


Estimated effective doses

       Estimate Std. Error   Lower   Upper
e:1:50   9.9953     1.3479  7.3536 12.6371

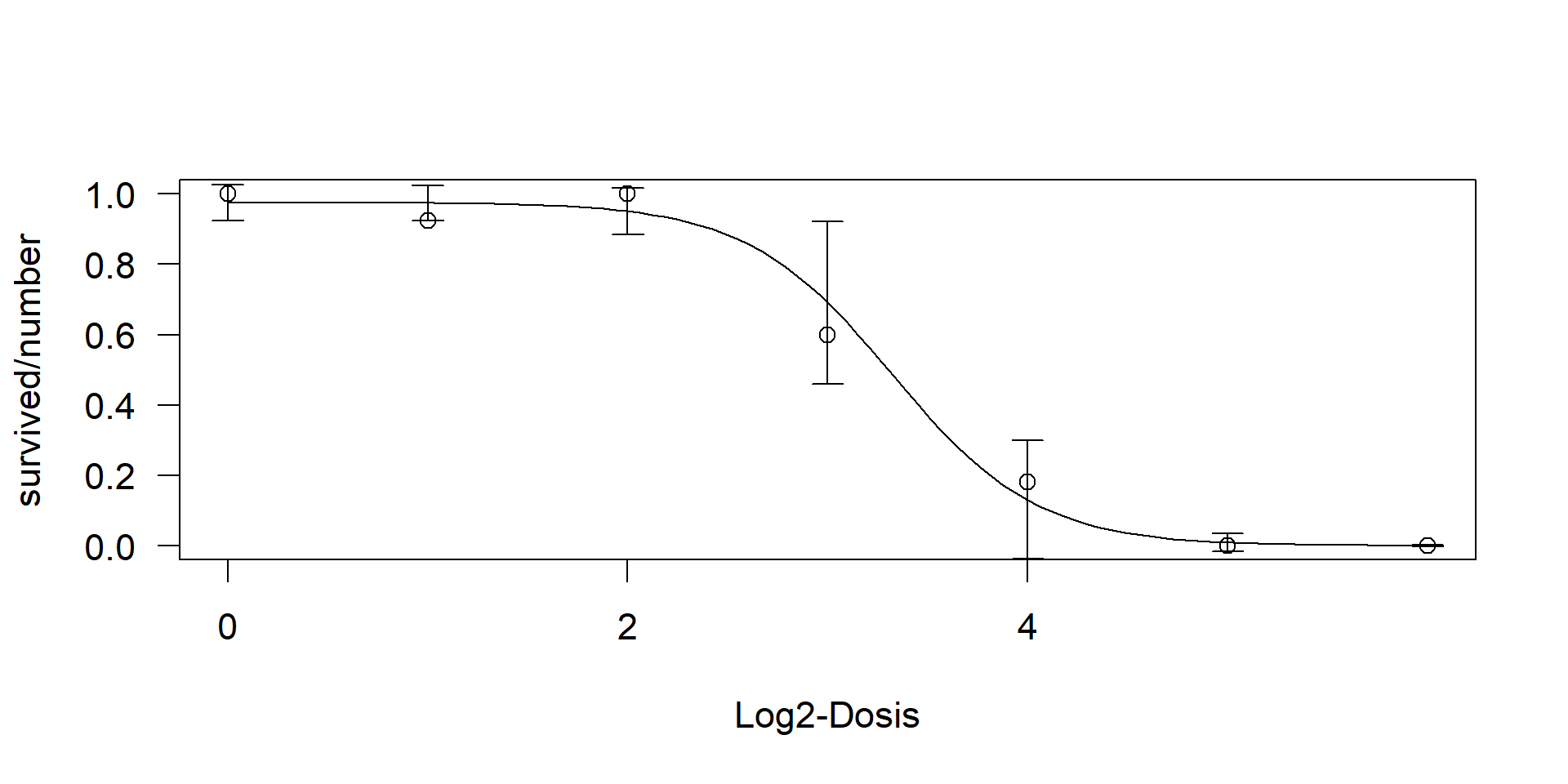
Schätzung von EC₅₀ und des CI ist mit drc direkter und robuster als mit glm.
CI an den Rändern nur approximativ (überschreitet Intervall (0, 1))

Zusammenfassung: Modellvergleich (GLM vs. drc)

GLM (Logistische Regression): fundamentale Grundlage zur Modellierung von Proportionen.
- Schätzt zwei Parameter (EC₅₀ und Steigung)
- Relativ starr, erzwingt eine Symmetrie um den EC₅₀
Dose Response Curves mit drc
- flexiblere log-logistische Modelle, z.B. (LL.3) mit drei Parametern
  (Steigung, EC₅₀, Asymptote).
- präzisere Anpassung an biologische Dosis-Wirkungs-Daten.

Modellvergleich: \(\rightarrow\) Füllen Sie folgende Tabelle aus:

Modell	EC₅₀	\(CI\) (lower, upper)
GLM (Linear Logit)	……	……, ……
drc (`LL.3`)	……	……, ……

Wichtig: Log-Transformation beachten und auf die Konzentrationsskala transformieren.

Binomiale ANCOVA

Ziel: Modellierung des Effekts einer kontinuierlichen Kovariaten (logdose) unter Berücksichtigung eines kategorialen Faktors (Substanz).

Szenario: Vergleich zweier Tox-Tests

Wir testen die Überlebensrate von Daphnien in Abhängigkeit von der Log-Dosis (dose_log) für zwei verschiedene Substanzen (Substanz A und Substanz B).

Response: Binär/Proportional (Überleben/Tod)
Kovariate (Kontinuierlich): Dosis oder log(Dosis)
Faktor (Kategorial): mehrere Substanzen oder Randbedingungen

Modellierung im GLM

Die ANCOVA-Struktur im GLM vergleicht drei Hypothesen:

A: Unabhängige Linien (Additive ANCOVA)

Das Modell nimmt an, dass die Substanzen die \(\text{LC}_{50}\) verschieben, aber die Steigung (Wirkstärke) gleich ist. Die Kurven sind parallel auf der Logit-Skala.

B: Interaktion (Vollständige ANCOVA)

Das Modell nimmt an, dass sich sowohl die EC₅₀ als auch die Steigung der Dosis-Wirkungs-Kurve zwischen den Substanzen unterscheiden.

Binomiale ANCOVA: Mehrere Substanzen gleichzeitig

Fragestellung: Sind die EC₅₀ von 2 Substanzen signifikant verschieden?

daphnia2 <- data.frame(
  dead = c(0, 0, 1, 3, 7, 9, 10, 
           1, 1, 3, 6, 9, 10, 10),
  total = 10,
  dose_log = rep(1:7, 2),
  substance = factor(rep(c("A", "B"), each = 7))
)

Verwendete Pakete

Zur Visualisierung könnte man sich eine “base graphics” zusammenbauen oder ggplot2 verwenden.
Im folgenden verwenden wir das Paket tinyplot (McDermott et al., 2025) sowie Pakete aus der easystats-Familie (Lüdecke et al., 2021, 2022).
Ein Vorteil von tinyplot ist, dass man darin direkt Modellformeln verwenden kann.

Code anzeigen

library("tinyplot")
plt(
  I(dead / total) ~ dose_log | substance,
  data = daphnia2,
  type = "p",
  main = "Daphnia: 2 Substances",
  ylab = "Proportion",
  grid = TRUE
)

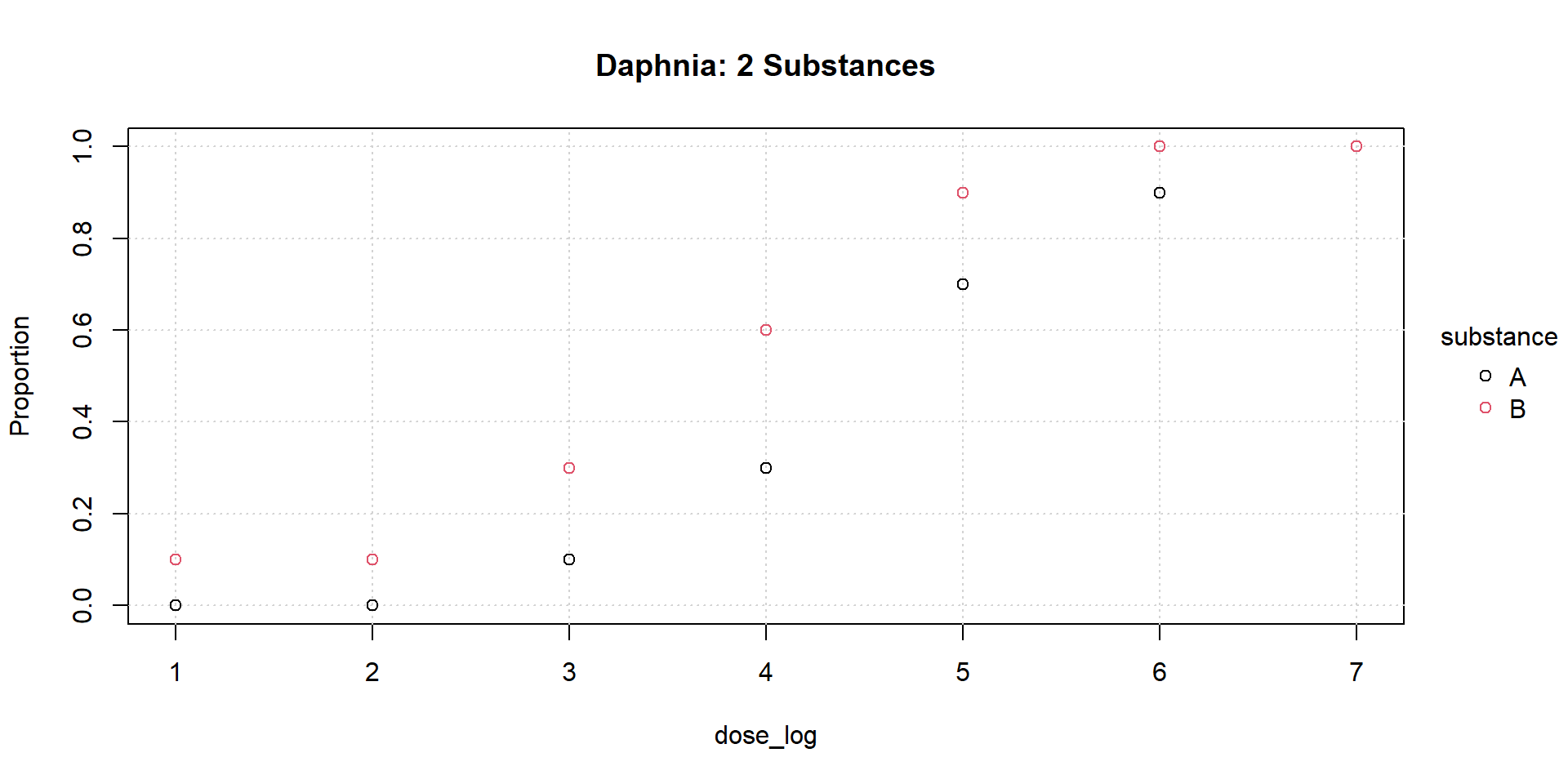
Fitten und Test einr Binomial-GLM-ANCOVA

m_AB <- glm(
  cbind(dead, total - dead) ~ dose_log * substance,
  data = daphnia2, 
  family = binomial(link = "logit")
)

anova(m_AB, test="Chi")

Analysis of Deviance Table

Model: binomial, link: logit

Response: cbind(dead, total - dead)

Terms added sequentially (first to last)

                   Df Deviance Resid. Df Resid. Dev Pr(>Chi)    
NULL                                  13    111.461             
dose_log            1  100.834        12     10.627  < 2e-16 ***
substance           1    7.215        11      3.412  0.00723 ** 
dose_log:substance  1    0.532        10      2.880  0.46586    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Visualisierung

Code anzeigen

# Interaction was not significant --> use model without interaaction (+)
m_AB<- glm(
  cbind(dead, total - dead) ~ dose_log + substance,
  data = daphnia2, 
  family = binomial(link = "logit")
)

# create range of doses for a smooth plot
dose_range <- seq(1, 7, length.out = 100)
newdata    <- expand.grid(dose_log = dose_range, substance = c("A", "B"))

# Predict probabilities using the model
newdata$prob <- predict(m_AB, newdata = newdata, type = "response")

# Plot the empirical proportions
plt(
  I(dead / total) ~ dose_log | substance,
  data = daphnia2,
  type = "p",
  main = "Daphnia: 2 Substances",
  ylab = "Proportion",
  grid = TRUE
)

# Overlay the GLM fit lines
plt(
  prob ~ dose_log | substance,
  data = newdata,
  type = "l",
  add = TRUE,    # 'add = TRUE' acts like base R's lines()
  lwd = 2
)
abline(h=0.5, col="grey")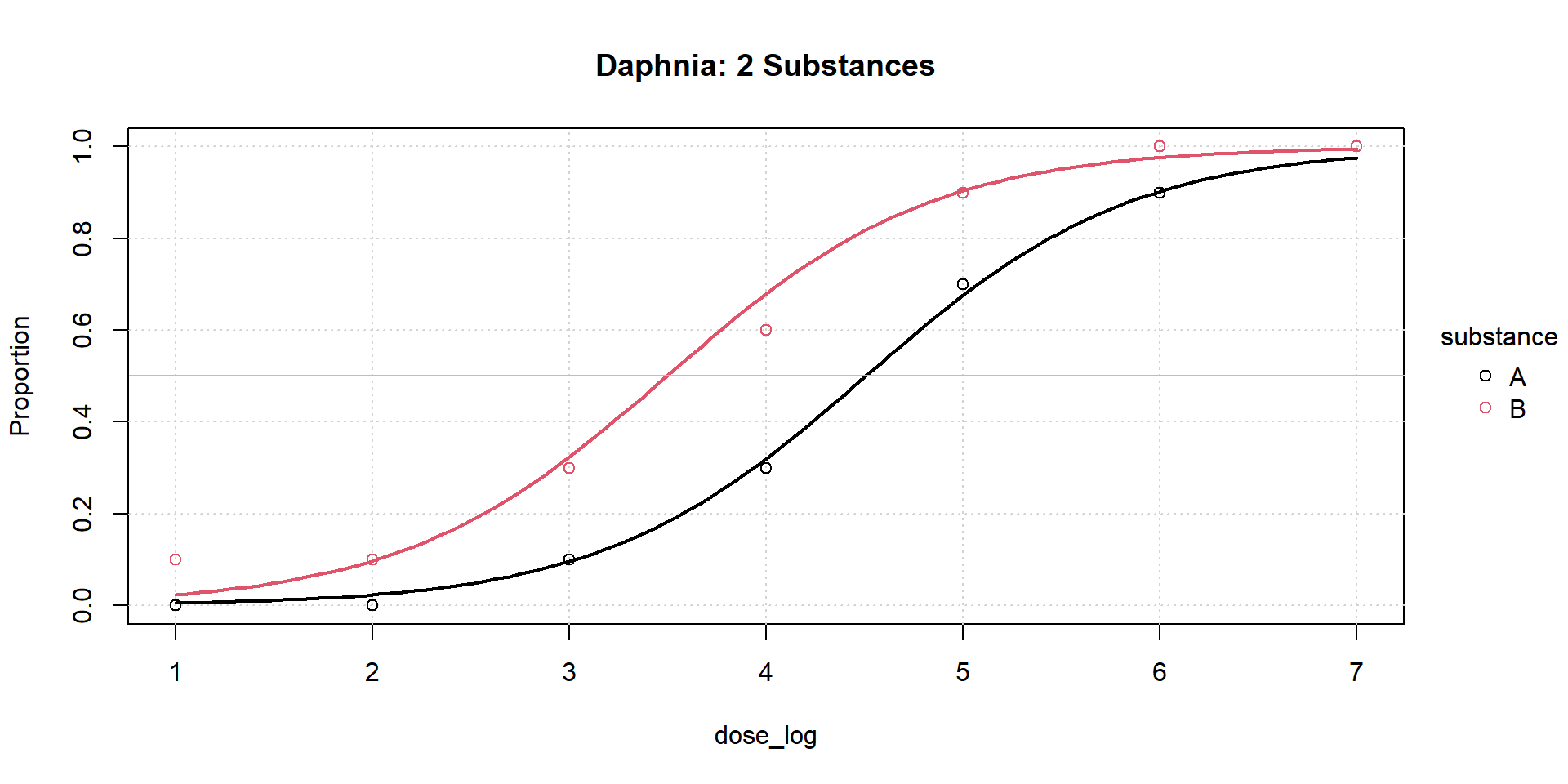

Diagnostik

library(performance)
library(see) # für bessere Plots
check_model(m_AB)

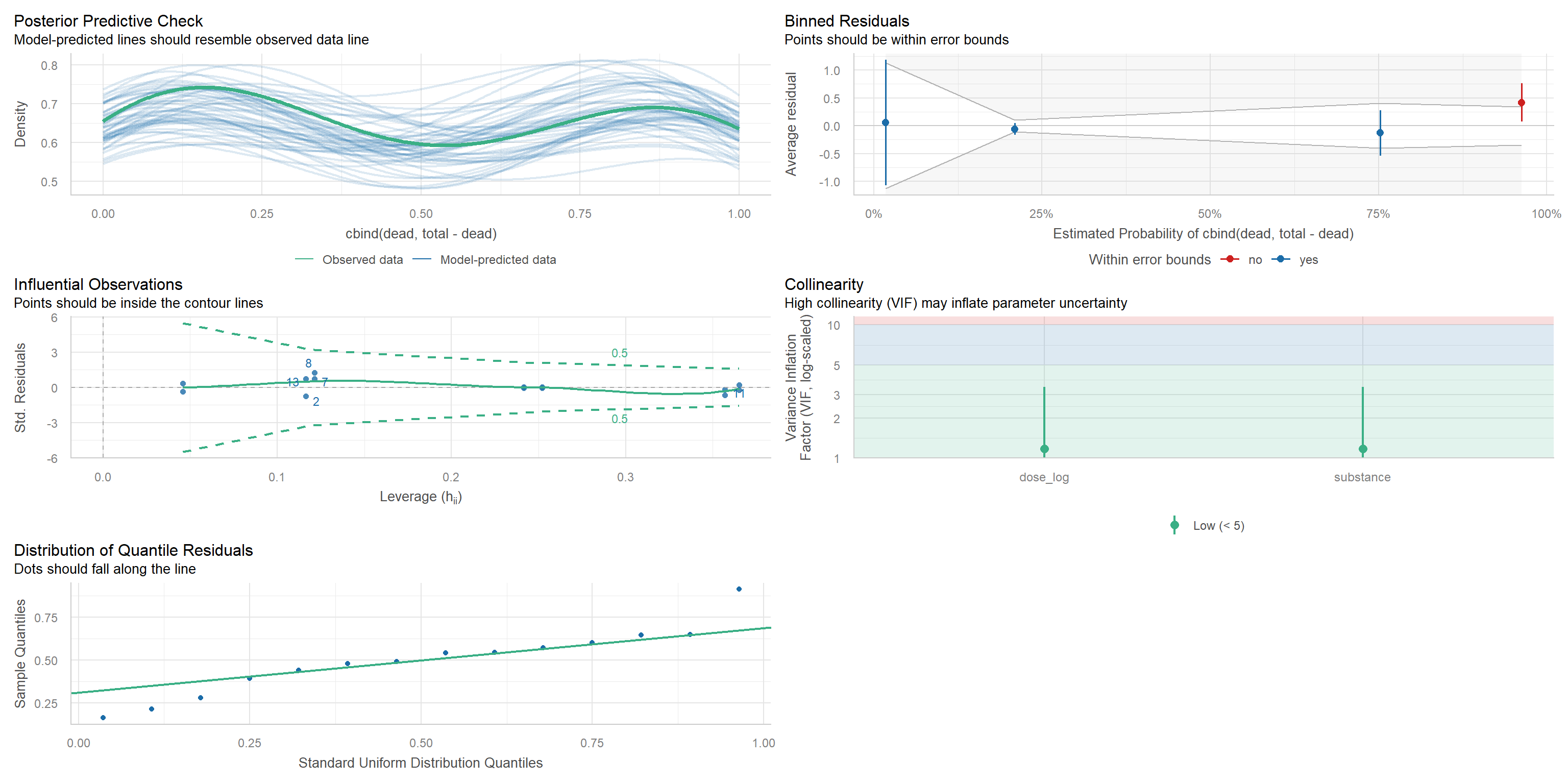
Modellparameter

Zusammenfassung der Koeffizienten mit CIs
Interpretation auf der Antwortskala (Wahrscheinlichkeit)

library(parameters)
mp <- model_parameters(m_AB, exponentiate=FALSE)
mp

Parameter     | Log-Odds |   SE |         95% CI |     z |      p
-----------------------------------------------------------------
(Intercept)   |    -6.70 | 1.15 | [-9.27, -4.71] | -5.84 | < .001
dose log      |     1.49 | 0.24 | [ 1.07,  2.03] |  6.16 | < .001
substance [B] |     1.50 | 0.60 | [ 0.39,  2.75] |  2.53 | 0.012

Schätzung der EC50

# Koeffizienten abrufen
b0 <- mp$Coefficient[mp$Parameter == "(Intercept)"]  # -6.70
b1 <- mp$Coefficient[mp$Parameter == "dose_log"]     # 1.49 (Steigung)
b2 <- mp$Coefficient[mp$Parameter == "substanceB"]   # 1.50 (Verschiebung)

# --- 1. EC50 auf der Log-Skala (log2(Dose)) ---
# A) EC50 für Substanz A (Referenz)
ec50_log_A <- -b0 / b1

# B) EC50 für Substanz B (mit Intercept-Verschiebung)
# (Formel gilt das additive Modell ohne Interaktion)
ec50_log_B <- -(b0 + b2) / b1

# --- 2. Rücktransformation auf die Konzentrationsskala ---
ec50_conc_A <- 2^ec50_log_A
ec50_conc_B <- 2^ec50_log_B

cat("EC50 (log2) A, B:", round(ec50_log_A, 2), round(ec50_log_B, 2), "\n")

EC50 (log2) A, B: 4.51 3.49

cat("EC50 (Conc) A, B:", round(ec50_conc_A, 1), round(ec50_conc_B, 1), "\n")

EC50 (Conc) A, B: 22.7 11.3

Zum Weiterlesen und Vertiefen

Für eine tiefere Einarbeitung in die statistische Modellierung mit den oben genannten und weiteren Methoden der ökologischen Statistik wird empfohlen:

Die Dosis-Wirkungs-Analyse mit dem R-Paket drc wird umfassend im Buch von Ritz et al. (2019) behandelt. Es enthält die Grundlagen und fortgeschrittene Techniken zur Modellierung nichtlinearer Kurven.
Das Buch von Crawley (2012) enthält neben klassischen statistischen Tests und ANOVA auch eine Reihe von Beispielen zur Anwendung von GLMs.
Das Buch von Zuur et al. (2009) zur Anwendung gemischter Modelle (Mixed Models) enthält u.a. auch Beispiele für GLMs, speziell ausgerichtet auf ökologische Fragestellungen.
Für eine moderne Sichtweise auf die Ökologische Statistik gibt der Sammelband von Fox et al. (2015) eine hervorragende Übersicht. Er verbindet aktuelle Theorie und praktische Anwendung in der ökologischen Forschung.

Literaturverzeichnis

Crawley, M. J. (2012). The r book (2nd ed.). John Wiley & Sons.

Fox, G. A., Negrete-Yankelevich, S., & Sosa, V. J. (Eds.). (2015). Ecological statistics: Contemporary theory and application. Oxford University Press.

Lüdecke, D., Ben-Shachar, M. S., Patil, I., Waggoner, P., & Makowski, D. (2021). performance: An R package for assessment, comparison and testing of statistical models. Journal of Open Source Software, 6(60), 3139. https://doi.org/10.21105/joss.03139

Lüdecke, D., Ben-Shachar, M. S., Patil, I., Wiernik, B. M., Bacher, E., Thériault, R., & Makowski, D. (2022). Easystats: Framework for easy statistical modeling, visualization, and reporting. CRAN. https://doi.org/10.32614/CRAN.package.easystats

McDermott, G., Arel-Bundock, V., & Zeileis, A. (2025). tinyplot: Lightweight extension of the base r graphics system. https://doi.org/10.32614/CRAN.package.tinyplot

Ritz, C., Baty, F., Streibig, J. C., & Gerhard, D. (2015). Dose-response analysis using r. PLOS ONE, 10(e0146021, 12). http://journals.plos.org/plosone/article?id=10.1371/journal.pone.0146021

Ritz, C., Jensen, S. M., Gerhard, D., & Streibig, J. C. (2019). Dose-response analysis using r. CRC Press.

Zuur, A. F., Ieno, E. N., Walker, N., Saveliev, A. A., & Smith, G. M. (2009). Mixed effects models and extensions in ecology with r. Springer.

09-Generalized Linear Models

Ausgewählte Beispiele

Was ist ein Generalisiertes Lineares Modell (GLM)?

Verteilungsfamilie und Linkfunktion

Typische Familien und Kanonische Linkfunktionen

Modellformel

GLM Datenstruktur im R-Code

A: Logischer Vektor (0/1)

B: Häufigkeits-Matrix

Anwendung: Toxizitätstest (Toxtest)

Fitten des Modells und statistischer Test

Visualisierung

Konfidenzintervalle

Numerische Schätzung der EC50

GLM Diagnostik: Residuen und Leverage

Diagnostik-Plots

Diagnostik: Einfluss und Residuen

A: Einflussreiche Punkte (Leverage)

B: Residuen-Analyse

Dosis-Wirkungs-Analyse mit drc

Analyse des Toxtests mit dem drc-Paket

Plot und ED50 bzw. EC50

Zusammenfassung: Modellvergleich (GLM vs. drc)

Binomiale ANCOVA

Szenario: Vergleich zweier Tox-Tests

Modellierung im GLM

Binomiale ANCOVA: Mehrere Substanzen gleichzeitig

Verwendete Pakete

Fitten und Test einr Binomial-GLM-ANCOVA

Visualisierung

Diagnostik

Modellparameter

Schätzung der EC50

Zum Weiterlesen und Vertiefen

Literaturverzeichnis

Plot und ED₅₀ bzw. EC₅₀