07-ANOVA und ANCOVA

Angewandte Statistik – Ein Praxiskurs

Thomas Petzoldt

2025-11-22

ANOVA - Varianzanalyse

• Prüfung komplexer Hypothesen als Ganzes, z.B.:
  • mehr als zwei Stichproben (Mehrfachtestproblem),
  • mehrere multiple Faktoren (Mehrfach- ANOVA)
  • Eliminierung von Kovariaten (ANCOVA)
  • feste und/oder zufällige Effekte (Varianzzerlegung, Modelle mit gemischten Effekten)
• Unterschiedliche Anwendungsszenarien:
  • explorative Anwendung: Welche Einflussfaktoren sind wichtig?
  • Signifikanztests
  • statistische Modellierung: Quantifizierung von Effekten und Abhängigkeiten.
• ANOVA-Verfahren basieren (meistens) auf linearen Modellen.

Ein Praxisbeispiel

Suche nach einem geeigneten Medium für Wachstumsexperimente mit Grünalgen

• Schulprojekt aus “Jugend Forscht”
• geeignet für Kurse in Schule und Studium
• preisgünstig, einfach zu handhaben

Idee

• Verwendung eines kommerziellen Düngers mit den Hauptnährstoffen N und P
• Mineralwasser mit Spurenelementen
• Enthält stilles Mineralwasser genügend \(\mathrm{CO_2}\)?
• testen, wie man die Verfügbarkeit von \(\mathrm{CO_2}\) für die Photosynthese verbessern kann

Anwendung

7 Verschiedene Behandlungen

1. Düngemittellösung in geschlossenen Flaschen
2. Düngemittellösung in offenen Flaschen (\(\mathrm{CO_2}\) aus der Luft)
3. Düngemittel + Zucker (organische C-Quelle)
4. Dünger + zusätzliches \(\mathrm{HCO_3^-}\) (Zusatz von \(\mathrm{CaCO_3}\) zu sprudelndem Mineralwasser)
5. Standard-Algenwachstumsmedium („Basalmedium“) zum Vergleich
6. Deionisiertes („destilliertes“) Wasser und
7. Leitungswasser zum Vergleich

Versuchsaufbau

• jede Behandlung mit 3 Wiederholungen
• randomisierte Platzierung auf dem Schüttler
• 16:8 Licht:Dunkel-Zyklus
• Transmissionsmessung direkt in den Flaschen mit einem selbstgebauten Messgerät

Ergebnisse

Dünger – offene Flasche – + Zucker – + CaCO3 – Basalmedium – A. dest – Leitungswasser

Der Datensatz

treat	replicate 1	replicate 2	replicate 3
Fertilizer	0.020	-0.217	-0.273
F. open	0.940	0.780	0.555
F.+sugar	0.188	-0.100	0.020
F.+CaCO3	0.245	0.236	0.456
Bas.med.	0.699	0.727	0.656
A.dest	-0.010	0.000	-0.010
Tap water	0.030	-0.070	NA

• Wachstum von Tag 2 bis Tag 6 (relative Einheiten)
• NA bedeutet „nicht verfügbar“, d.h. ein fehlender Wert
• Die Kruztabelle ist kompakt und übersichtlich, jedoch nicht ideal für die Datenanalyse.
• \(\Rightarrow\) Konvertierung in das Langformat

Daten im Langformat

Vorteile

• sieht „unpraktisch“ aus, ist aber viel besser für die Datenanalyse
• abhängige Variable Wachstum und
  Erklärungsvariable Behandlung deutlich sichtbar
• Modellformel: growth ~ treat
• leicht erweiterbar auf \(>1\) Erklärungsvariable

treat	rep	growth
Fertilizer	1	0.020
Fertilizer	2	-0.217
Fertilizer	3	-0.273
F. open	1	0.940
F. open	2	0.780
F. open	3	0.555
F.+sugar	1	0.188
F.+sugar	2	-0.100
F.+sugar	3	0.020
F.+CaCO3	1	0.245
F.+CaCO3	2	0.236
F.+CaCO3	3	0.456

Die Daten in R

algae <- data.frame(
  treat  = factor(c("Fertilizer", "Fertilizer", "Fertilizer", 
             "F. open", "F. open", "F. open", 
             "F.+sugar", "F.+sugar", "F.+sugar", 
             "F.+CaCO3", "F.+CaCO3", "F.+CaCO3", 
             "Bas.med.", "Bas.med.", "Bas.med.", 
             "A.dest", "A.dest", "A.dest", 
             "Tap water", "Tap water"),
             levels=c("Fertilizer", "F. open", "F.+sugar", 
                    "F.+CaCO3", "Bas.med.", "A.dest", "Tap water")),
  rep   = c(1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3, 1, 2), 
  growth = c(0.02, -0.217, -0.273, 0.94, 0.78, 0.555, 0.188, -0.1, 0.02, 
             0.245, 0.236, 0.456, 0.699, 0.727, 0.656, -0.01, 0, -0.01, 0.03, -0.07)
)

• Kleine Datensätze können direkt in den Code eingebunden werden.
• Eine csv-Datei im Langformat ist ebenfalls möglich.
• Wichtig: treat als Faktor (nominale Variable).
• Mit levels kann man die Reihenfolge fixieren.

Boxplot

boxplot(growth ~ treat, data = algae)
abline(h = 0, lty = "dashed", col = "grey")

Streifendiagramm

stripchart(growth ~ treat, data = algae, vertical = TRUE)

Besser als Boxplot, denn wir haben nur 2-3 Wiederholungen. Boxplot braucht mehr.

Umwandlung einer wissenschaftlichen Frage in eine statistische Hypothese

Wissenschaftliche Fragen

• Sind die Behandlungen unterschiedlich?
• Welches Medium ist das beste?
• Ist das beste Medium signifikant besser als die anderen?
• Wieviel besser ist das beste Medium (Efektstärke)?

Statistische Hypothesen

• \(H_0\): das Wachstum ist bei allen Behandlungen gleich
• \(H_A\): Unterschiede zwischen den Medien

Warum nicht einfach mehrere t-Tests?

• Wenn wir bei 7 Behandlungen jede gegen jede testen wollen, brauchen wir:

\[7 \cdot (7 - 1) / 2 = 21 \qquad\text{Tests.}\]

• Bei \(\alpha = 0.05\), erhält man 5% falsch positive Ergebnisse.
  \(\Rightarrow\) Einer von 20 Tests ist im Durchschnitt falsch positiv.
• Bei \(N\) Tests erhöht sich der Gesamtfehler von \(\alpha\) im schlimmsten Fall auf \(N\cdot\alpha\).
• Dies wird alpha-Fehler-Inflation oder Bonferroni-Ungleichung genannt:

\[ \alpha_{total} \le \sum_{i=1}^{N} \alpha_i = N \cdot \alpha \]

Wird die Regel ignoriert, erhält man zufällige falsch-positive Ergebnisse (statistical fishing).

Lösungsansätze

1. Korrektur der Alpha-Fehler, so dass \(\alpha_{total} = 0.05\) bleibt;
   \(\rightarrow\) Bonferroni-Regel.
2. Verfahren, das das Gesamtproblem behandelt:
   \(\rightarrow\) ANOVA.

ANOVA: Varianzanalyse

Grundgedanke

• Aufteilung der Gesamtvarianz in Wirkung(en) und Fehler:

\[ s_y^2 = s^2_\mathrm{effect} + s^2_{\varepsilon} \]

• Etwas überraschend: Analyse von Varianzen, um Mittelwerte zu vergleichen.
• Erklärung: Mittelwertunterschiede tragen zur Gesamtvarianz der ganzen Stichprobe bei.
• Die Varianzkomponenten können als Varianz innerhalb (\(s^2_\varepsilon\)) und Varianz zwischen Stichproben bezeichnet werden.
• Die Varianz-Zerlegung erfolgt über ein lineares Modell.

Beispiel

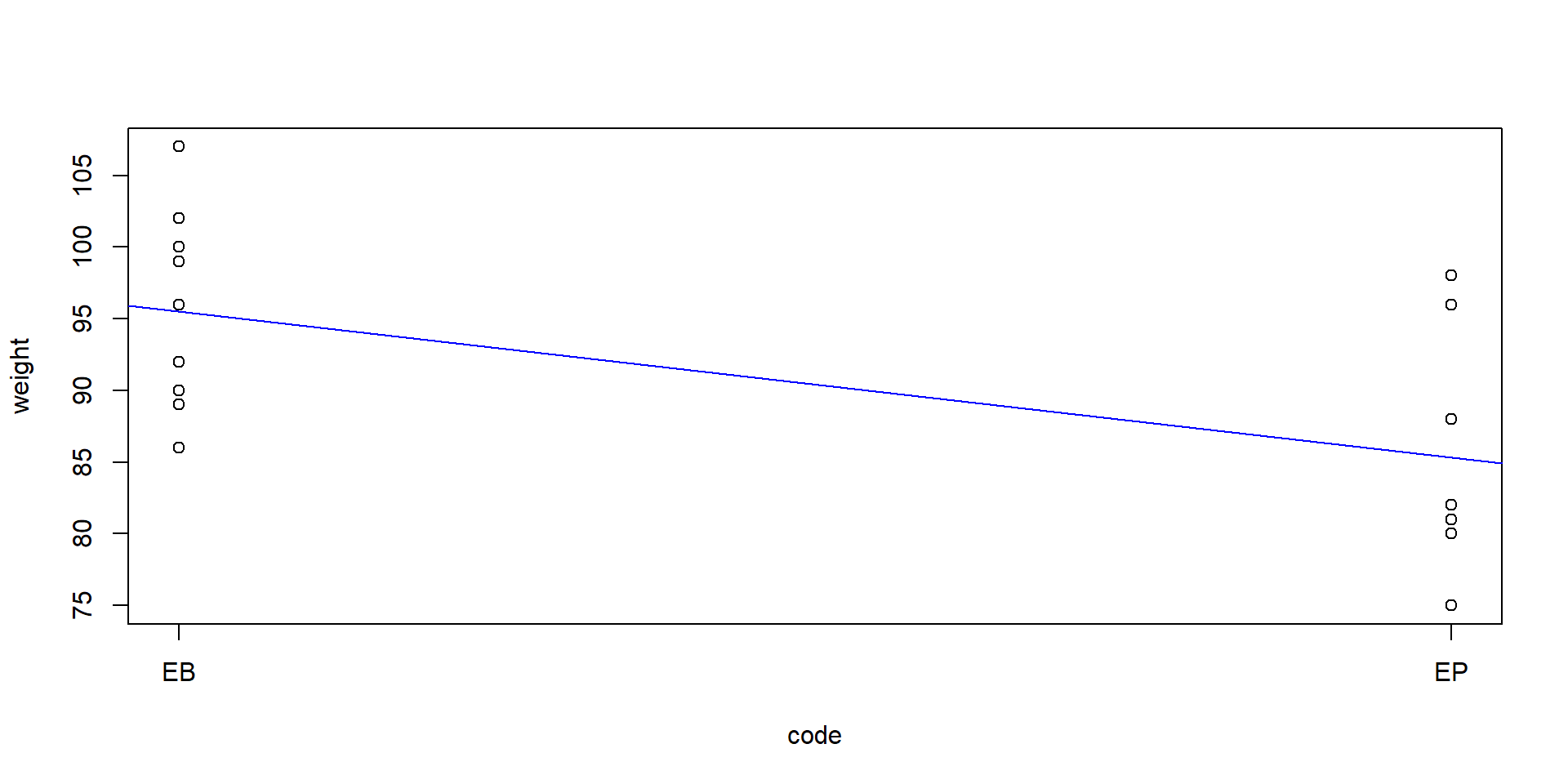
Zwei Marken von Clementinen aus einem Geschäft „E“, die wir als „EB“ und „EP“ bezeichnen. Wir wollen wissen, ob die Premiummarke („P“) und die Basismarke („B“) ein unterschiedliches Gewicht haben.

clem <- data.frame(
  brand = c("EP", "EB", "EB", "EB", "EB", "EB", "EB", "EB", "EB", "EB", "EB", 
            "EB", "EB", "EB", "EP", "EP", "EP", "EP", "EP", "EP", "EP", "EB", "EP"),
  weight = c(88, 96, 100, 96, 90, 100, 92, 92, 102, 99, 86, 89, 99, 89, 75, 80, 
             81, 96, 82, 98, 80, 107, 88))

Wir kodieren eine Stichprobe („EB“) mit 1 und die andere Stichprobe („EP“) mit 2:

clem$code <- as.numeric(factor(clem$brand))
clem$code

 [1] 2 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 1 2

Dann wird eine lineare Regression angewandt

plot(weight ~ code, data = clem, axes = FALSE)
m <- lm(weight ~ code, data = clem)
axis(1, at = c(1,2), labels = c("EB", "EP")); axis(2); box()
abline(m, col = "blue")

Lineares Modell und Varianzkomponenten

m <- lm(weight ~ code, data = clem)

Gesamtvarianz

(var_tot <- var(clem$weight))

[1] 68.98814

Restvarianz (= Varianz innerhalb der Behandlungen)

(var_res <- var(residuals(m)))

[1] 43.25

Erklärte Varianz (= Varianz zwischen den Behandlungen)

var_tot - var_res

[1] 25.73814

• Das Beispiel zeigt das Grundprinzip.
• Aber: Die „erklärte Varianz“ ist nicht für den F-Test der ANOVA geeignet, weil die Freiheitsgrade nicht berücksichtigt sind.

Korrekte Berechnung mit Freiheitsgraden

# Freiheitsgrade
n <- nrow(clem)
k <- length(unique(clem$brand))

df_total     <- n - 1      # -1 df für den Gesamtmittelwert (Intercept)
df_between   <- k - 1      # df für Gruppenunterschiede (nach Berücksichtigung des Gesamtmittelwerts)
df_residuals <- n - k      # -1 df pro Gruppe (insgesamt k Gruppen)
# Prüfung: df_total sollte gleich df_between + df_residuals sein
c(n = n, k = k, df_total = df_total, df_between = df_between, df_residuals = df_residuals)

           n            k     df_total   df_between df_residuals 
          23            2           22            1           21 

# Sums of squares
SS_total     <- var_tot * df_total
SS_residuals <- var_res * df_total  # var(residuals) nutzt n−1
SS_between   <- SS_total - SS_residuals

# Mean sums of squares
MS_between   <- SS_between / df_between
MS_residuals <- SS_residuals / df_residuals
c(MS_between = MS_between, MS_residuals = MS_residuals)

  MS_between MS_residuals 
   566.23913     45.30952 

# F-Test
F_stat <- MS_between / MS_residuals
p_val  <- pf(F_stat, df1 = df_between, df2 = df_residuals, lower.tail = FALSE)

c(F = round(F_stat, 3), p = round(p_val, 4))

     F      p 
12.497  0.002 

Die ANOVA arbeitet direkt mit den Summen der Quadrate, ohne den Umweg über die Varianzen.

ANOVA in einem Schritt

anova(m)

Analysis of Variance Table

Response: weight
          Df Sum Sq Mean Sq F value   Pr(>F)   
code       1 566.24  566.24  12.497 0.001963 **
Residuals 21 951.50   45.31                    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Ein t-Test zum Vergleich

t.test(weight ~ code, data = clem, var.equal=TRUE)

    Two Sample t-test

data:  weight by code
t = 3.5351, df = 21, p-value = 0.001963
alternative hypothesis: true difference in means between group 1 and group 2 is not equal to 0
95 percent confidence interval:
  4.185911 16.147423
sample estimates:
mean in group 1 mean in group 2 
       95.50000        85.33333 

\(\Rightarrow\) Die p-Werte sind identisch.

• Bei zwei Gruppen ist die ANOVA (F-Test) äquivalent zum t-Test mit gleichen Varianzen.
• \(F = t^2\), \(p\) gleich.

ANOVA mit mehr als 2 Stichproben

Zurück zum Algenwachstums-Experiment:

m <- lm(growth ~ treat, data = algae)

• Wir könnten die Koeffizienten mit summary(m) ausgeben.
• Zunächst interessiert uns der Gesamteffekt, daher verwenden wir anova(m).

anova(m)

Analysis of Variance Table

Response: growth
          Df  Sum Sq Mean Sq F value    Pr(>F)    
treat      6 2.35441 0.39240  25.045 1.987e-06 ***
Residuals 13 0.20368 0.01567                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• zeigt den F-Test für den Gesamteffekt des Faktors treat.

\(\Rightarrow\) Der p-Wert ist sehr klein → der Behandlungseffekt ist signifikant.

Posthoc-Tests

• Der F-Test zeigte, dass der Faktor „Behandlung“ einen signifikanten Effekt hat.
• Wir wissen jedoch noch nicht, welche spezifischen Gruppen sich unterscheiden.
• Tukey-HSD-Test (HSD = Honest Significant Difference): am häufigsten verwendeter Post-hoc-Test für ANOVA.
  
• vergleicht alle Paare von Gruppen und berücksichtigt die family-wise error rate.

tk <- TukeyHSD(aov(m))
tk

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = m)

$treat
                            diff         lwr         upr     p adj
F. open-Fertilizer    0.91500000  0.56202797  1.26797203 0.0000103
F.+sugar-Fertilizer   0.19266667 -0.16030537  0.54563870 0.5211198
F.+CaCO3-Fertilizer   0.46900000  0.11602797  0.82197203 0.0069447
Bas.med.-Fertilizer   0.85066667  0.49769463  1.20363870 0.0000231
A.dest-Fertilizer     0.15000000 -0.20297203  0.50297203 0.7579063
Tap water-Fertilizer  0.13666667 -0.25796806  0.53130140 0.8837597
F.+sugar-F. open     -0.72233333 -1.07530537 -0.36936130 0.0001312
F.+CaCO3-F. open     -0.44600000 -0.79897203 -0.09302797 0.0102557
Bas.med.-F. open     -0.06433333 -0.41730537  0.28863870 0.9943994
A.dest-F. open       -0.76500000 -1.11797203 -0.41202797 0.0000721
Tap water-F. open    -0.77833333 -1.17296806 -0.38369860 0.0001913
F.+CaCO3-F.+sugar     0.27633333 -0.07663870  0.62930537 0.1727182
Bas.med.-F.+sugar     0.65800000  0.30502797  1.01097203 0.0003363
A.dest-F.+sugar      -0.04266667 -0.39563870  0.31030537 0.9994197
Tap water-F.+sugar   -0.05600000 -0.45063473  0.33863473 0.9985686
Bas.med.-F.+CaCO3     0.38166667  0.02869463  0.73463870 0.0307459
A.dest-F.+CaCO3      -0.31900000 -0.67197203  0.03397203 0.0879106
Tap water-F.+CaCO3   -0.33233333 -0.72696806  0.06230140 0.1247914
A.dest-Bas.med.      -0.70066667 -1.05363870 -0.34769463 0.0001792
Tap water-Bas.med.   -0.71400000 -1.10863473 -0.31936527 0.0004507
Tap water-A.dest     -0.01333333 -0.40796806  0.38130140 0.9999997

Grafische Darstellung

par(las = 1)              # Achsenbeschriftungen horizontal
par(mar = c(4, 10, 3, 1)) # mehr Platz für lange Gruppenbezeichnungen
plot(tk)

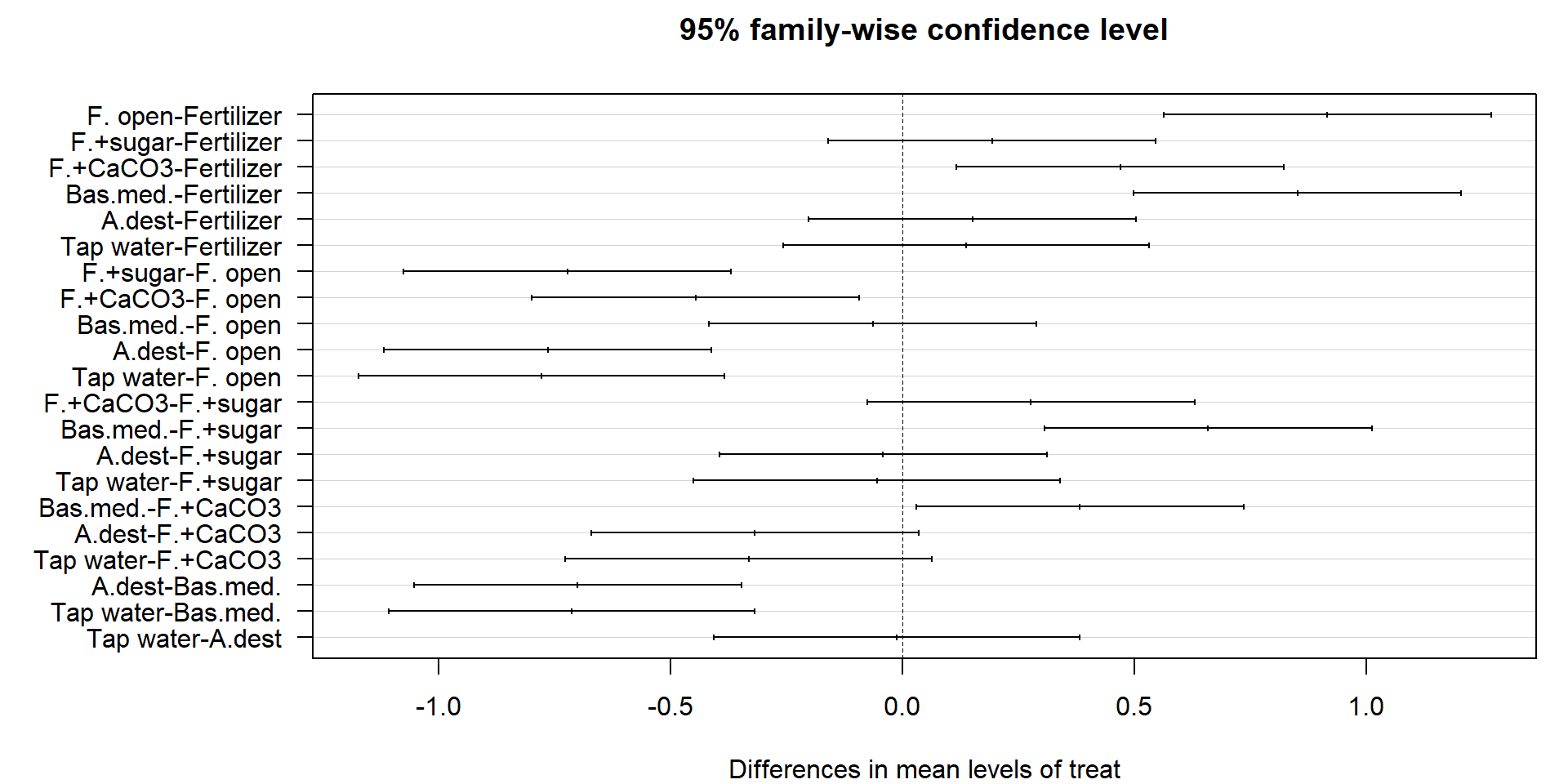
ANOVA Annahmen und Diagnostik

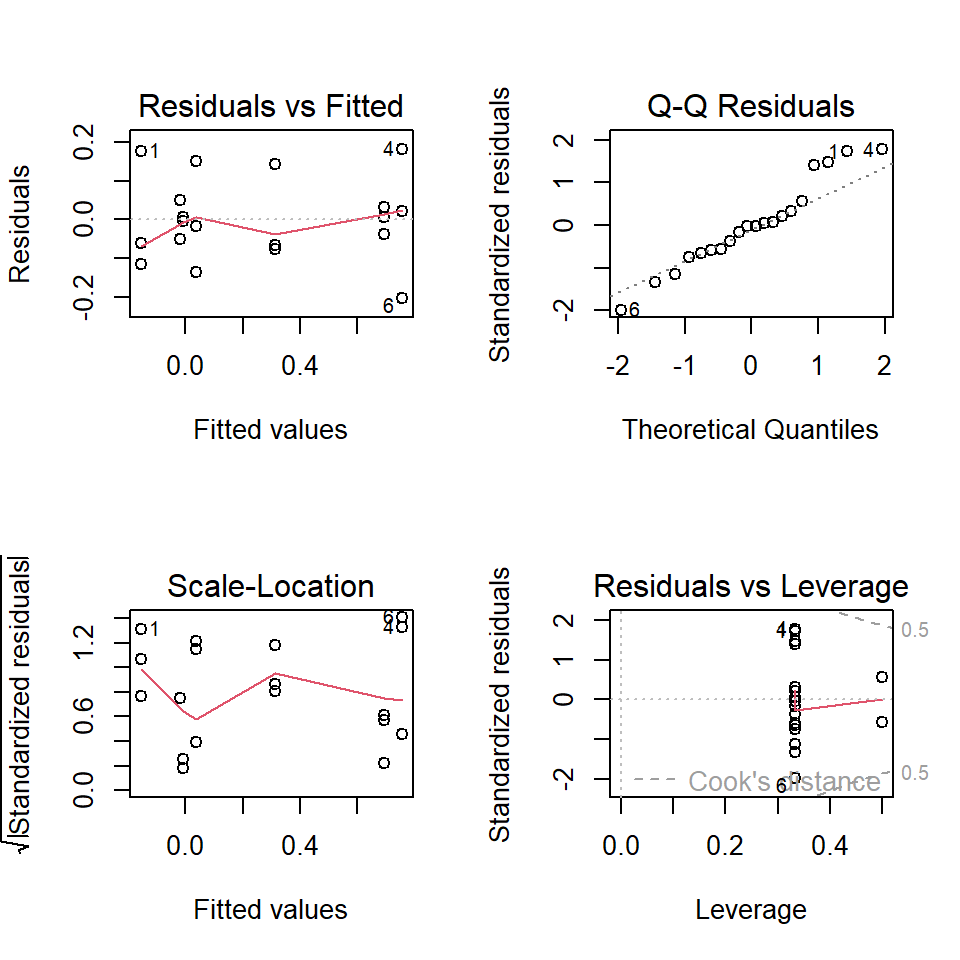
Für die ANOVA gelten dieselben Annahmen wie für das lineare Modell.

1. Unabhängigkeit der Fehler
2. Homogenität der Varianzen (Homoskedastizität)
3. Annähernde Normalverteilung der Fehler

Grafische Diagnostik wird bevorzugt – sie ist robuster als numerische Tests.

par(mfrow=c(2, 2))
plot(m)

Test der Varianzhomogenität

• Der F-Test ist nur für zwei Gruppen geeignet.
• Für mehr als zwei Gruppen: Bartlett-, Levene- oder Fligner-Killeen-Test.
• Empfohlen: Fligner-Killeen-Test - robust gegenüber Abweichung von Normalverteilung.

fligner.test(growth ~ treat, 
             data = algae)

    Fligner-Killeen test of homogeneity of variances

data:  growth by treat
Fligner-Killeen:med chi-squared = 4.2095, df = 6, p-value = 0.6483

Test auf Normalverteilung

• Teste die Residuen, nicht die Rohdaten!
• Der Shapiro-Wilk-Test wird nicht mehr empfohlen:
  • Bei kleinen Stichproben: hohe Wahrscheinlichkeit für Fehlertyp II
    (keine Ablehnung, obwohl Unterschiede existieren).
  • Bei großen Stichproben: hohe Wahrscheinlichkeit für Fehlertyp I
    (Ablehnung, obwohl Unterschiede vernachlässigbar sind.)
• Empfohlen: Grafische Methoden – insbesondere der QQ-Plot.

qqnorm(residuals(m))
qqline(residuals(m))

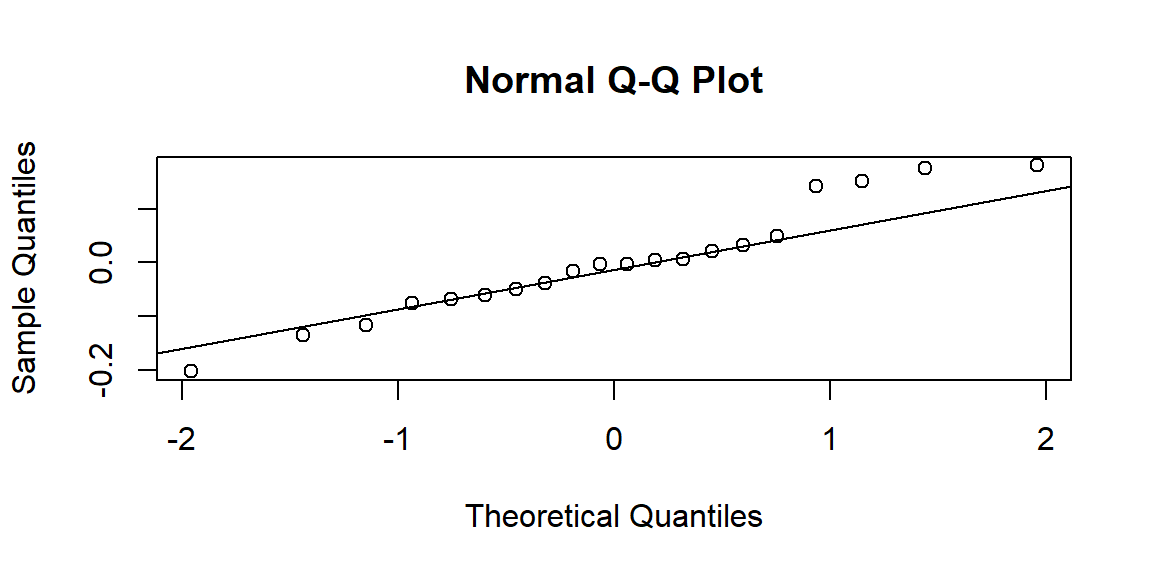
Moderne Sichtweise: Keine Vortests mehr!

Die traditionelle Praxis – Residuen zu testen, bevor man ANOVA durchführt –
ist nicht mehr zeitgemäß und führt zu gravierenden Problemen:

• Residuen sind erst nach Modellanpassung verfügbar.
• Bei Vortests müsste man sie „irgendwie vorher“ schätzen, oft durch Pooling.
• Häufig wurden Rohdaten statt Residuen getestet - Kardinalfehler.
• Die Methode stammt aus der Ära manueller Berechnungen.

Empfohlene Vorgehensweise:

1. Prüfe, ob ANOVA grundsätzlich angemessen ist:
   • Fragestellung,
   • Unabhängigkeit,
   • mögliche Nichtnormalität auf Grund des Versuchsdesigns
2. Führe die ANOVA durch – ohne Vortests.
3. Diagnostik im Anschluss – grafisch und kritisch (QQ-Plot, Residuals vs. Fitted).

Einfache ANOVA mit heterogenen Varianzen

• Erweiterung des Welch-Tests für \(\ge 2\) Stichproben
• in R oneway.test genannt.

oneway.test(growth ~ treat, data = algae)

    One-way analysis of means (not assuming equal variances)

data:  growth and treat
F = 115.09, num df = 6.0000, denom df = 4.6224, p-value = 6.57e-05

• Der oneway.test berücksichtigt ungleiche Varianzen durch gewichtete Mittelwerte und Freiheitsgrade und eine angepasste F-Statistik.
• Die Varianzhomogenität ist wichtiger als die Normalverteilung – insbesondere bei unbalancierten Designs.
• Ein Varianzunterschied kann den F-Test stärker verzerren als leichte Abweichungen von der Normalverteilung.

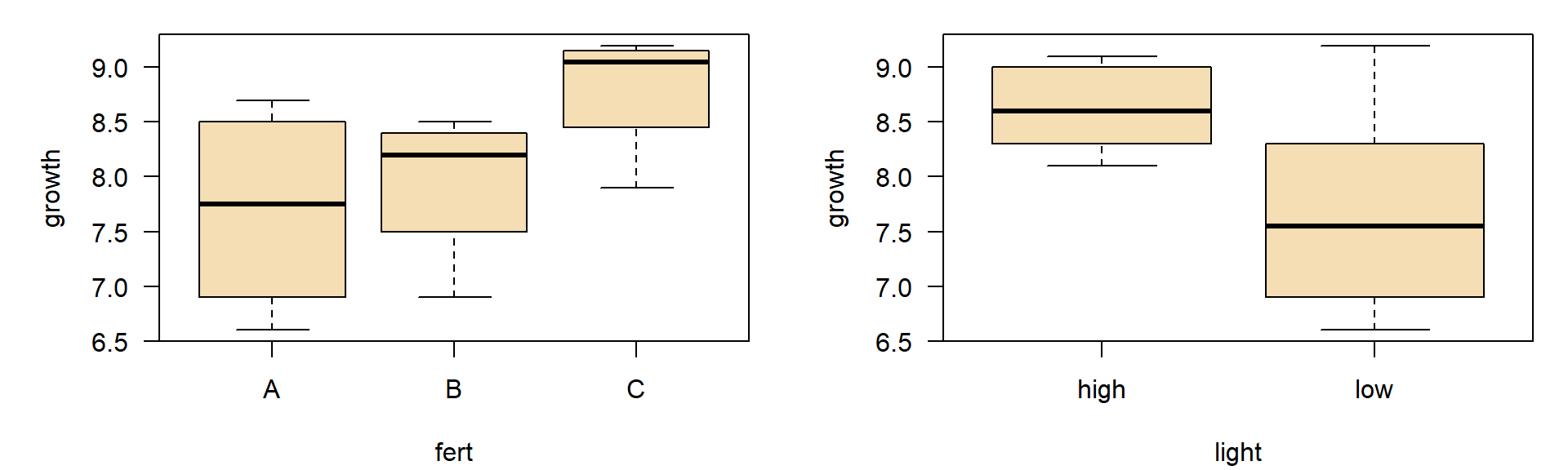
Zweifache ANOVA

• Beispiel aus einem Statistik-Lehrbuch (Crawley, 2002), angewandt auf einen neuen Kontext
• Auswirkungen von Dünger und Licht auf das Wachstum der Pflanzenhöhe in cm pro Zeit

Dünger	helles Licht	schwaches Licht
A	8.3	6.6
A	8.7	7.2
B	8.1	6.9
B	8.5	8.3
C	9.1	7.9
C	9.0	9.2

• faktorielles Experiment (mit Wiederholungen)
• für jede Faktorkombination mehr als eine Beobachtung
• Es können Wechselwirkungen identifiziert werden

Falls keine Wiederholungen: Keine Schätzung des Fehlers für Interaktionen - keine Identifizierung von Wechselwirkungen möglich.

Daten im Langformat eingeben

plants <- data.frame(No = 1:12,
                    growth = c(6.6, 7.2, 6.9, 8.3, 7.9, 9.2,
                               8.3, 8.7, 8.1, 8.5, 9.1, 9.0),
                    fert   = rep(c("A", "B", "C"), each=2),
                    light  = rep(c("low", "high"), each=6)
          )

No	growth	fert	light
1	6.6	A	low
2	7.2	A	low
3	6.9	B	low
4	8.3	B	low
5	7.9	C	low
6	9.2	C	low
7	8.3	A	high
8	8.7	A	high
9	8.1	B	high
10	8.5	B	high
11	9.1	C	high
12	9.0	C	high

Beispiele für Modellformeln

Modell Typ	Formel
Nullmodell	y ~ 1
Einfache lineare Regression	y ~ x
Linear ohne Achsenschnittpunkt	y ~ x - 1
Multiple Regression, keine Interaktion	y ~ x1 + x2 + x3
Multiple Regression mit Interaktion	y ~ x1 * x2 * x3
… ohne 3-fache Interaktion	y ~ x1 * x2 * x3 - x1 : x2 : x3
Transformiert mit I() (‘as is’)	y ~ x + I(x^2)
Einfache ANOVA	y ~ f
ANOVA mit Interaktion	y ~ f1 * f2
ANCOVA mit Interaktion	y ~ x * f
Verschachtelte ANOVA	y ~ x + (1 | a / b)
GAM mit glättendem s	y ~ s(x) + f

• y = Antwortvariable (abhängige, target)
• x = metrische Erklärungsvariable (Prädiktor, unabhängig)
• f = Faktorvariable (nominal)

Lineares Modell und ANOVA

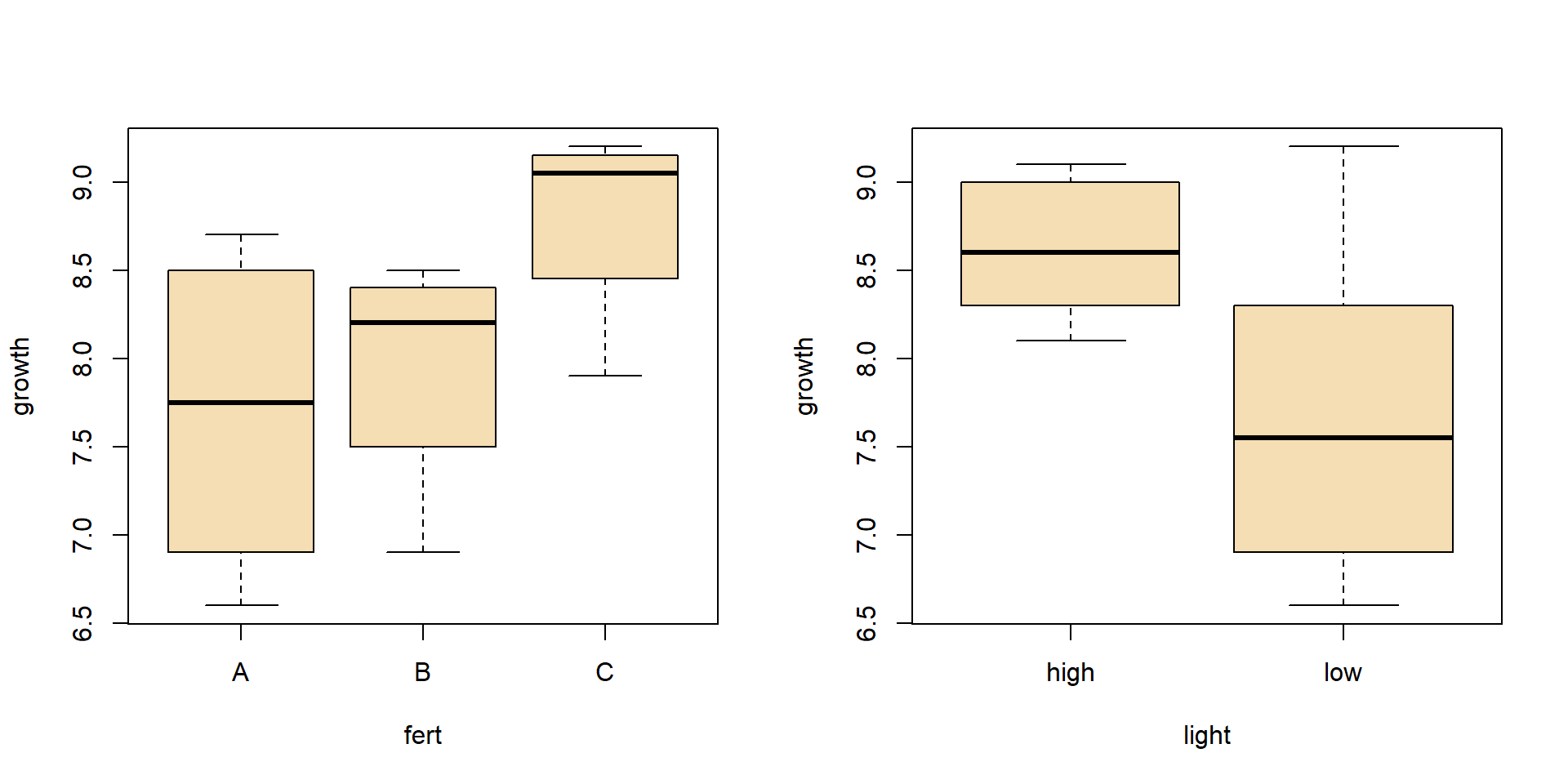
ANOVA

m <- lm(growth ~ light * fert, data = plants)
anova(m)

Analysis of Variance Table

Response: growth
           Df  Sum Sq Mean Sq F value  Pr(>F)  
light       1 2.61333 2.61333  7.2258 0.03614 *
fert        2 2.66000 1.33000  3.6774 0.09069 .
light:fert  2 0.68667 0.34333  0.9493 0.43833  
Residuals   6 2.17000 0.36167                  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Interaktionsplot

with(plants, interaction.plot(fert, light, growth, 
                            col = c("orange", "brown"), lty = 1, lwd = 2))

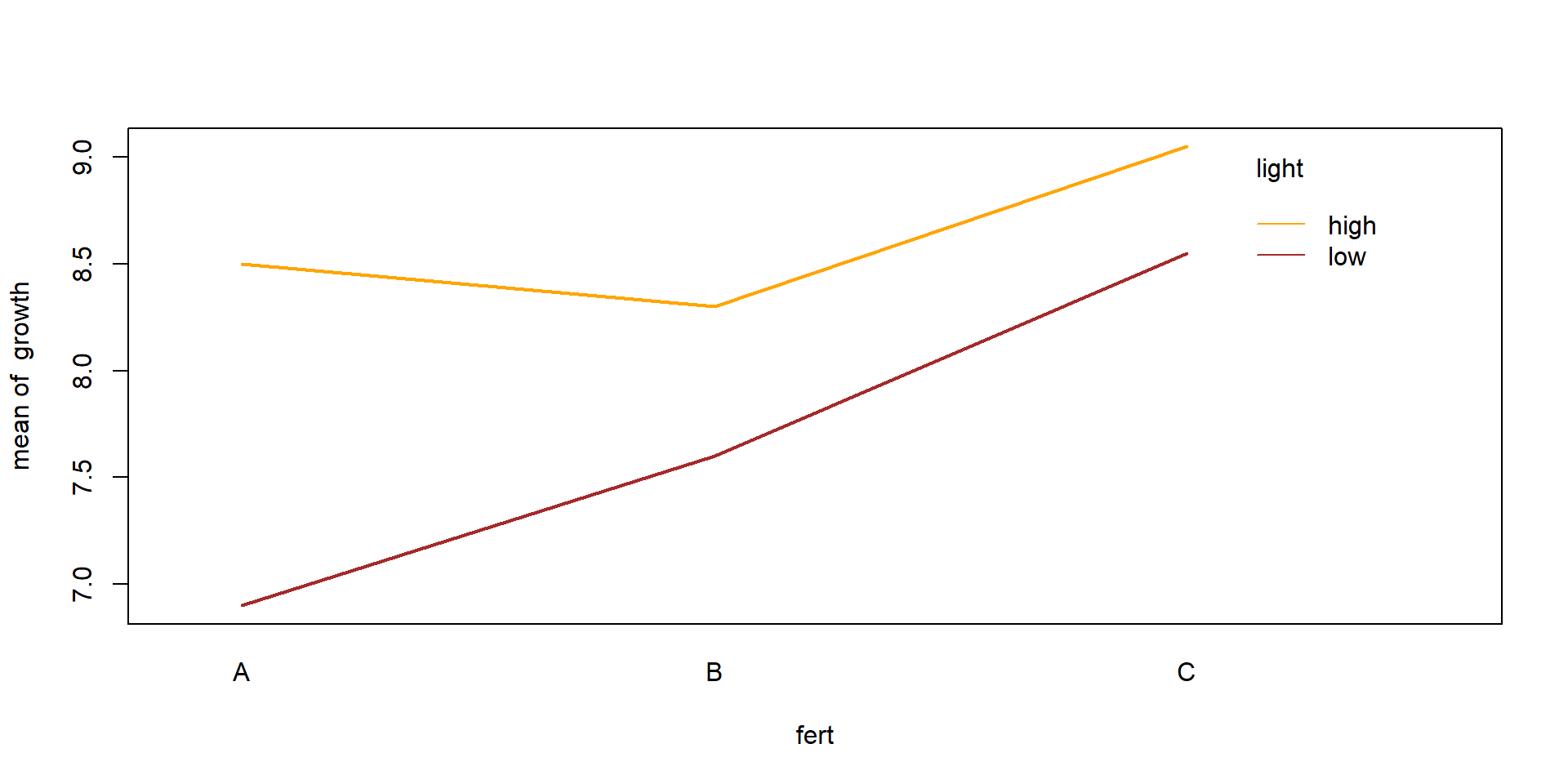
• Wenn die Linien nicht parallel sind, deutet es auf eine Wechselwirkung hin.

Diagnostik

1. Unabhängigkeit der Messungen (innerhalb der Gruppen)
2. Homogenität der Varianz der Residuen
3. Normalverteilung der Residuen

Der Test der Annahmen benötigt Residuen des angepassten Modells.

\(\Rightarrow\) Passe zuerst das ANOVA-Modell an und prüfe dann, ob es richtig war!

Diagnostikinstrumente

• Boxplot (Gruppenvergleich)
  
• Residuen vs. Fitted
• Q-Q-Diagramm der Residuen
  
• Fligner-Killeen-Test (von manchen wird alternativ der Levene-Test empfohlen)

Diagnostik II

par(mfrow=c(1, 2))
par(cex=1.2, las=1)
qqnorm(residuals(m))
qqline(residuals(m))

plot(residuals(m)~fitted(m))
abline(h=0)

fligner.test(growth ~ interaction(light, fert), data=plants)

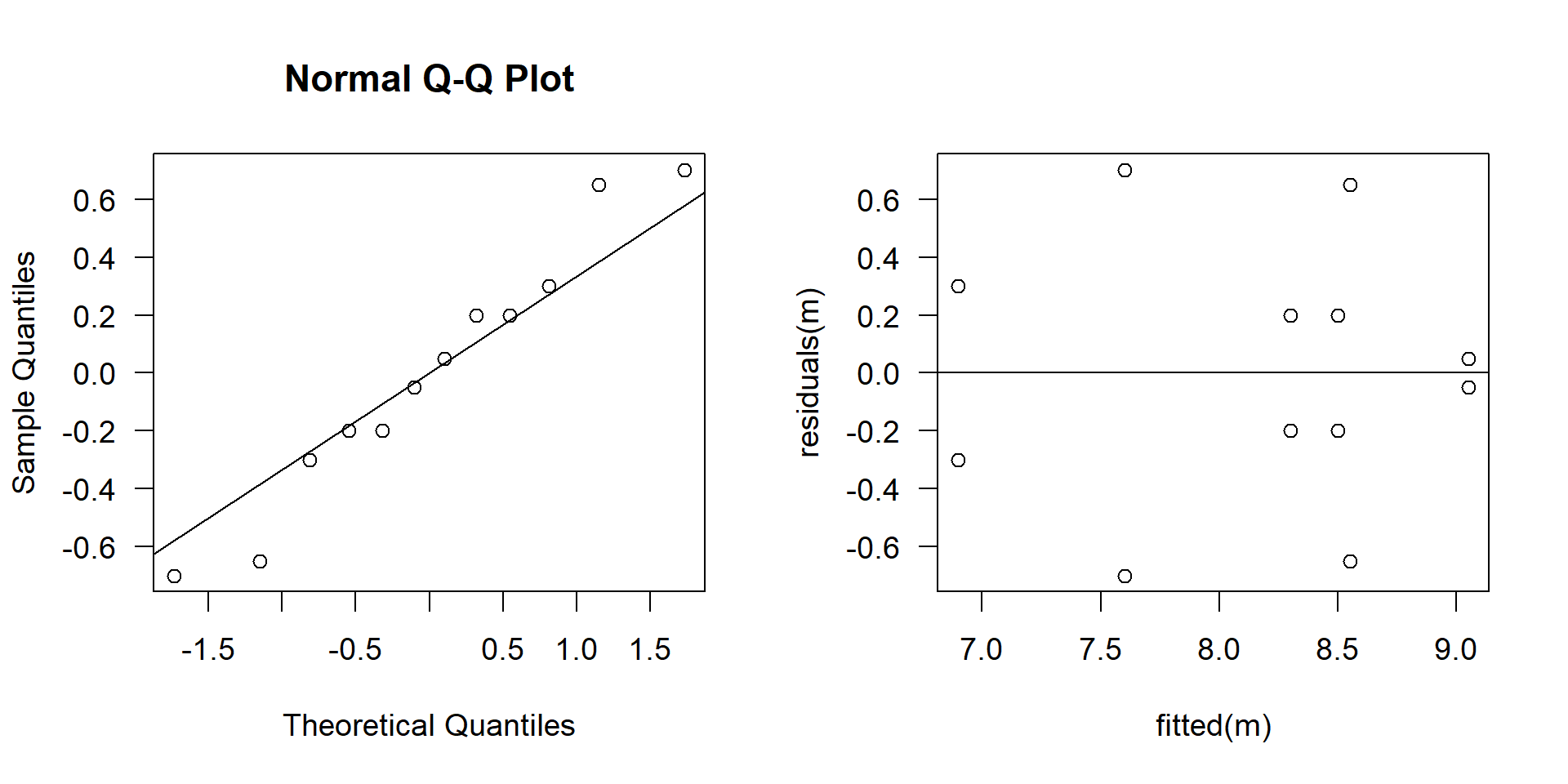
    Fligner-Killeen test of homogeneity of variances

data:  growth by interaction(light, fert)
Fligner-Killeen:med chi-squared = 10.788, df = 5, p-value = 0.05575

Residuen: sehen in Ordnung aus und der p-Wert des Fligner-Tests ist noch ok.

Anmerkungen

Lineare Regression oder ANOVA?

• Im Wesentlichen dasselbe Modell - nur unterschiedliche Sichtweise
• Metrische unabhängige Variablen → lineares Modell
  
• Nominalskalierte unabhängige Variablen (Faktoren) → ANOVA
  
• Mischung aus beidem → ANCOVA

Pre-Tests sind theoretisch und praktisch fragwürdig

1. Eine Nullhypothese \(H_0\) kann nicht bestätigt, sondern nur verworfen werden.
   
2. Bei großen Stichproben ist die Normalität der Residuen nicht zwingend erforderlich.
3. Wenn \(p\) in der Nähe des Schwellenwerts liegt und der Stichprobenumfang klein ist, bleiben wir im Ungewissen.

• All dies lässt sich nur durch sorgfältiges Nachdenken, Erfahrung und kritische Reflexion überwinden.
• Es ist immer eine gute Idee, die Ergebnisse mit anderen zu besprechen – nicht nicht um die Entscheidung zu delegieren, sondern um sie zu verstehen und zu verteidigen.

Sequentielles Holm-Bonferroni-Verfahren

• Auch bekannt als Holm-Korrektur (Holm, 1979)
• Einfach zu verwenden
• Kann auf jedes Problem mit Mehrfachtests angewendet werden
• Weniger konservativ als die normale Bonferroni-Korrektur, aber …
• … immer noch ein sehr konservativer Ansatz
• siehe auch Wikipedia

Algorithmus

1. Wähle den kleinsten \(p\)-Wert aus allen \(n\) \(p\)-Werten
2. Wenn \(p \cdot n < \alpha\) \(\Rightarrow\) signifikant, sonst STOPP
3. Setze \(n - 1 \rightarrow n\), entferne das kleinste \(p\) aus der Liste und gehe zu Schritt 1.

Der Algorithmus ist sequenziell

• Er prüft die Hypothesen in der Reihenfolge der kleinsten \(p\)-Werte.

Beispiel

Wachstumsrate pro Tag (\(d^{-1}\)) von Blaualgenkulturen (Pseudanabaena) nach Zugabe toxischer Peptide einer anderen Blaualge (Microcystis).

Die ursprüngliche Hypothese:

• Microcystin LR (MCYST) oder ein Derivat davon (Substanz A) hemmt das Wachstum.

mcyst <-  data.frame(treat = factor(c(rep("Control", 5),
                                       rep("MCYST", 5),
                                       rep("Subst A", 5)),
                                levels=c("Control", "MCYST", "Subst A")),
                      mu   = c(0.086, 0.101, 0.086, 0.086, 0.099,
                               0.092, 0.088, 0.093, 0.088, 0.086,
                               0.095, 0.102, 0.106, 0.106, 0.106)
                     )

Ansatz 1: einfache ANOVA

par(mar=c(4, 8, 2, 1), las=1)
m <- lm(mu ~ treat, data=mcyst)
anova(m)

Analysis of Variance Table

Response: mu
          Df     Sum Sq    Mean Sq F value   Pr(>F)   
treat      2 0.00053293 2.6647e-04   8.775 0.004485 **
Residuals 12 0.00036440 3.0367e-05                    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

plot(TukeyHSD(aov(m)))

Ansatz 2: multiple t-Tests mit sequentieller Bonferroni-Korrektur

Wir trennen den Datensatz in einzelne Teilmengen:

Control <- mcyst$mu[mcyst$treat == "Control"]
MCYST   <- mcyst$mu[mcyst$treat == "MCYST"]
SubstA  <- mcyst$mu[mcyst$treat == "Subst A"]

und führen 3 t-Tests durch:

p1 <- t.test(Control, MCYST)$p.value
p2 <- t.test(Control, SubstA)$p.value
p3 <- t.test(MCYST, SubstA)$p.value

p-Werte ohne Korrektur:

c(p1, p2, p3)

[1] 0.576275261 0.027378832 0.001190592

Mit Holm-Korrektur:

p.adjust(c(p1, p2, p3))

[1] 0.576275261 0.054757664 0.003571775

Schlussfolgerungen

Statistische Methoden

• Beim Holm-korrigierten t-Test bleibt nur ein einziger p-Wert (MCYST vs. Subst A) signifikant, bei der ANOVA sind es zwei.
• ANOVA berücksichtigt Struktur der Daten und die Abhängigkeit der Vergleiche.
• Holm-Methode konservativer als TukeyHSD \(\Rightarrow\) ANOVA + Posthoc ist zu bevorzugen.

Interpretation hinsichtlich der ursprünglichen Hypothese

• MCYST und Subst A hemmen das Wachstum von Pseudanabaena nicht.

• Im Gegenteil: Subst A stimuliert das Wachstum.

• Widerspruch zur Erwartung: der biologische Grund wurde 10 Jahre später entdeckt.

• Wichtig: Statistische Signifikanz sagt nichts über die biologische Relevanz aus.

• Falsche Hypothesen können zu falschen Erwartungen führen - oder zu neuen Entdeckungen.

Mehr dazu in Jähnichen et al. (2001), Jähnichen et al. (2007), Jähnichen et al. (2011), Zilliges et al. (2011), Dziallas & Grossart (2011), Wei et al. (2024)

ANCOVA

Statistische Frage

• Vergleich von Regressionslinien zwischen Gruppen
• Ähnlich wie bei der ANOVA, enthält aber auch metrische Variablen (Kovariaten)
• Haben Gruppen unterschiedliche Anfangswerte (Intercept) und/oder unterschiedliche Steigungen (Slope)?

Beispiel

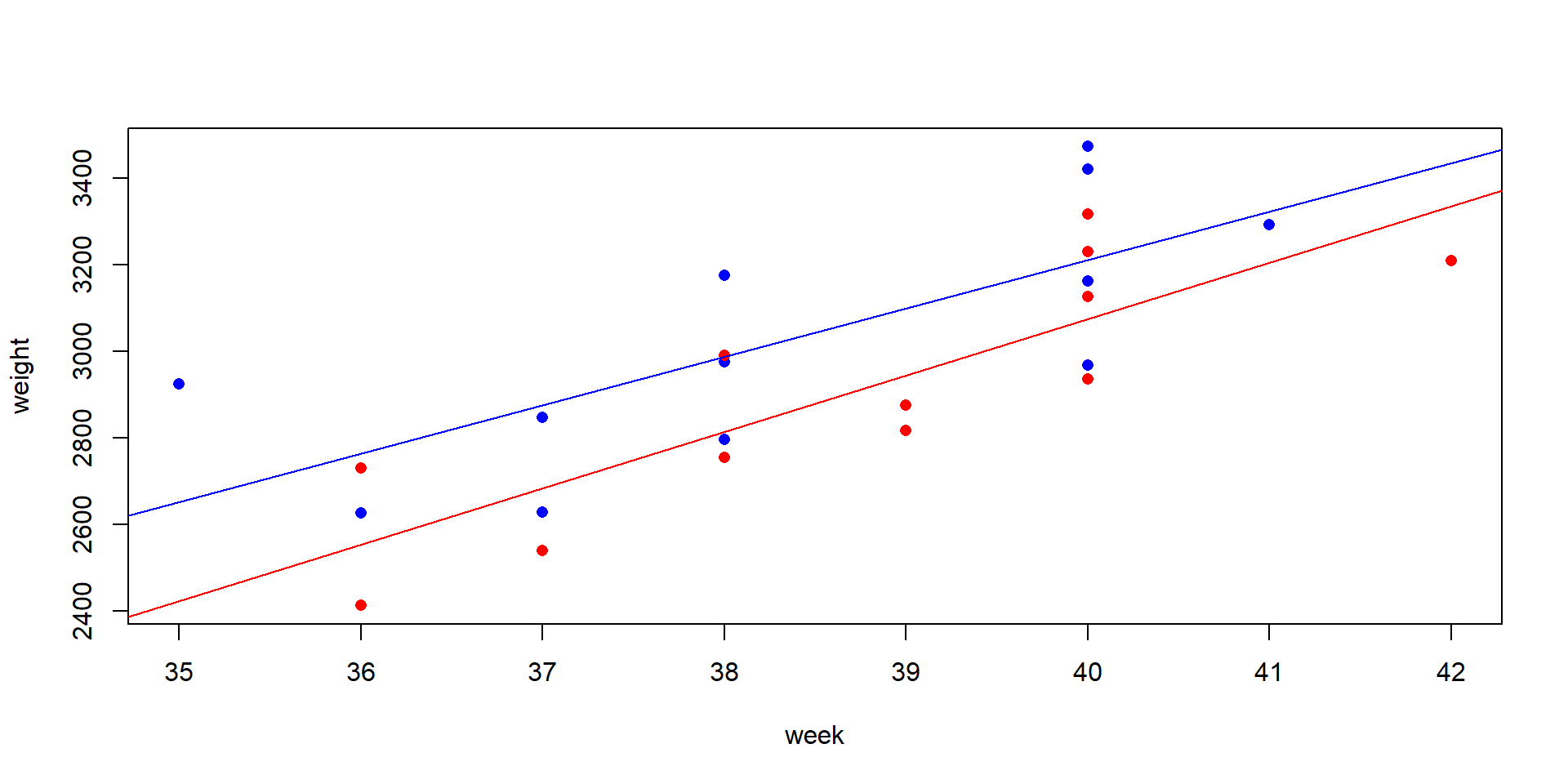
Annette Dobsons Geburtsgewichts-Daten – aus einem Statistik-Lehrbuch (Dobson, 2013): Geburtsgewicht von Jungen und Mädchen in Abhängigkeit von der Schwangerschaftswoche.

Der Datensatz zum Geburtsgewicht

Dieser Datensatz ist künstlich – nicht realistisch, aber ideal für die Demonstration.

Er ist in der R-Demo demo(lm.glm) enthalten.

## Daten zum Geburtsgewicht siehe stats/demo/lm.glm.R
dobson <- data.frame(
  week   = c(40, 38, 40, 35, 36, 37, 41, 40, 37, 38, 40, 38,
             40, 36, 40, 38, 42, 39, 40, 37, 36, 38, 39, 40),
  weight = c(2968, 2795, 3163, 2925, 2625, 2847, 3292, 3473, 2628, 3176,
             3421, 2975, 3317, 2729, 2935, 2754, 3210, 2817, 3126, 2539,
             2412, 2991, 2875, 3231),
  gender = gl(2, 12, labels = c("M", "F")) # generate factor levels
)

Warum nicht einfach einen t-Test durchführen?

boxplot(weight ~ gender,data = dobson, ylab = "weight")

t.test(weight ~ gender, data = dobson, var.equal = TRUE)

    Two Sample t-test

data:  weight by gender
t = 0.97747, df = 22, p-value = 0.339
alternative hypothesis: true difference in means between group M and group F is not equal to 0
95 percent confidence interval:
 -126.3753  351.7086
sample estimates:
mean in group M mean in group F 
       3024.000        2911.333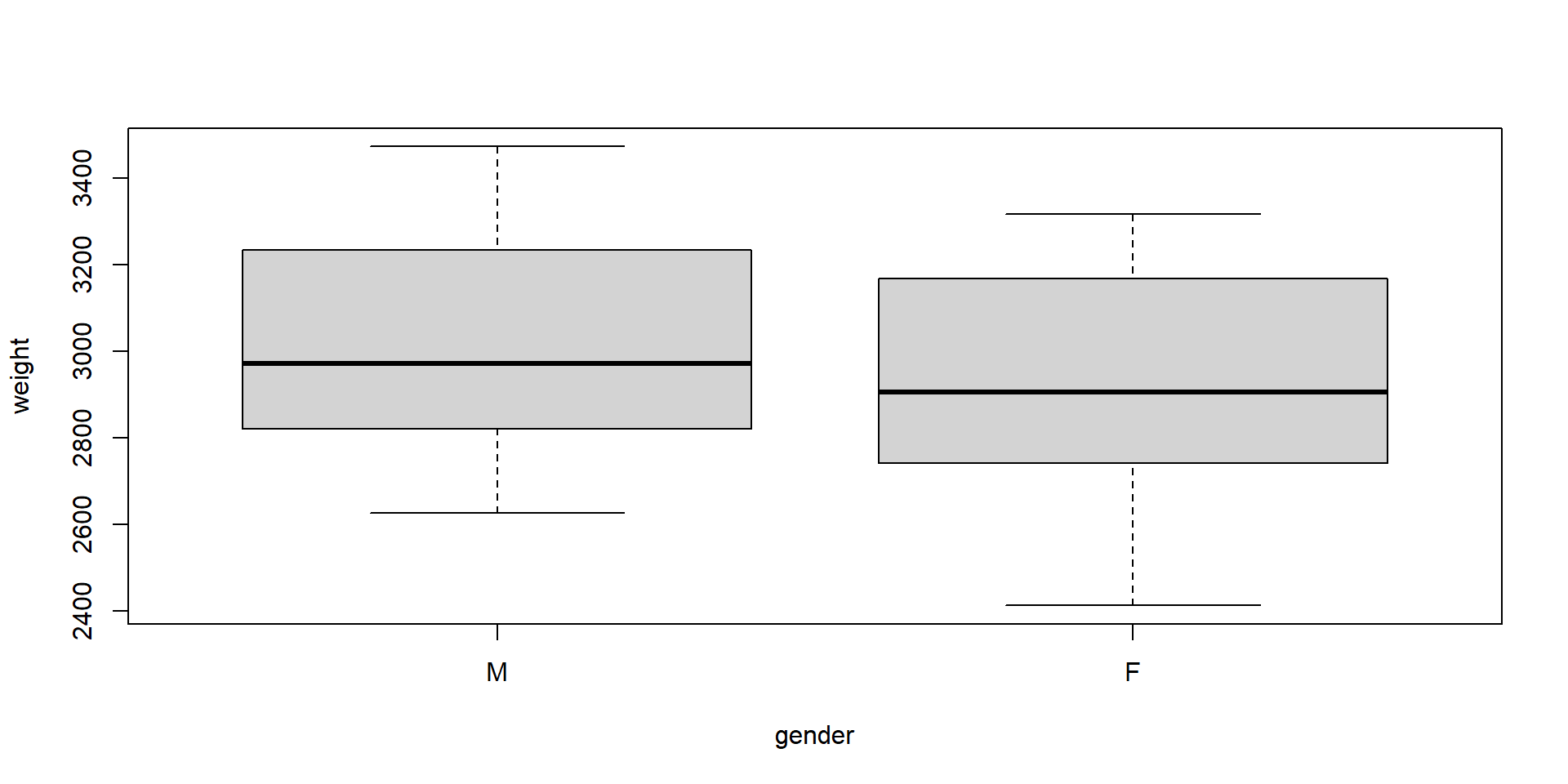 

• Der t-Test zeigt keine signifikante Differenz und der Boxplot zeigt starke Überlappung.
• Aber: Der t-Test ignoriert die Schwangerschaftswoche, eine wichtige Kovariate.

ANCOVA: Berücksichtigung der Kovariate

m <- lm(weight ~ week * gender, data = dobson)
anova(m)

Analysis of Variance Table

Response: weight
            Df  Sum Sq Mean Sq F value    Pr(>F)    
week         1 1013799 1013799 31.0779 1.862e-05 ***
gender       1  157304  157304  4.8221   0.04006 *  
week:gender  1    6346    6346  0.1945   0.66389    
Residuals   20  652425   32621                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1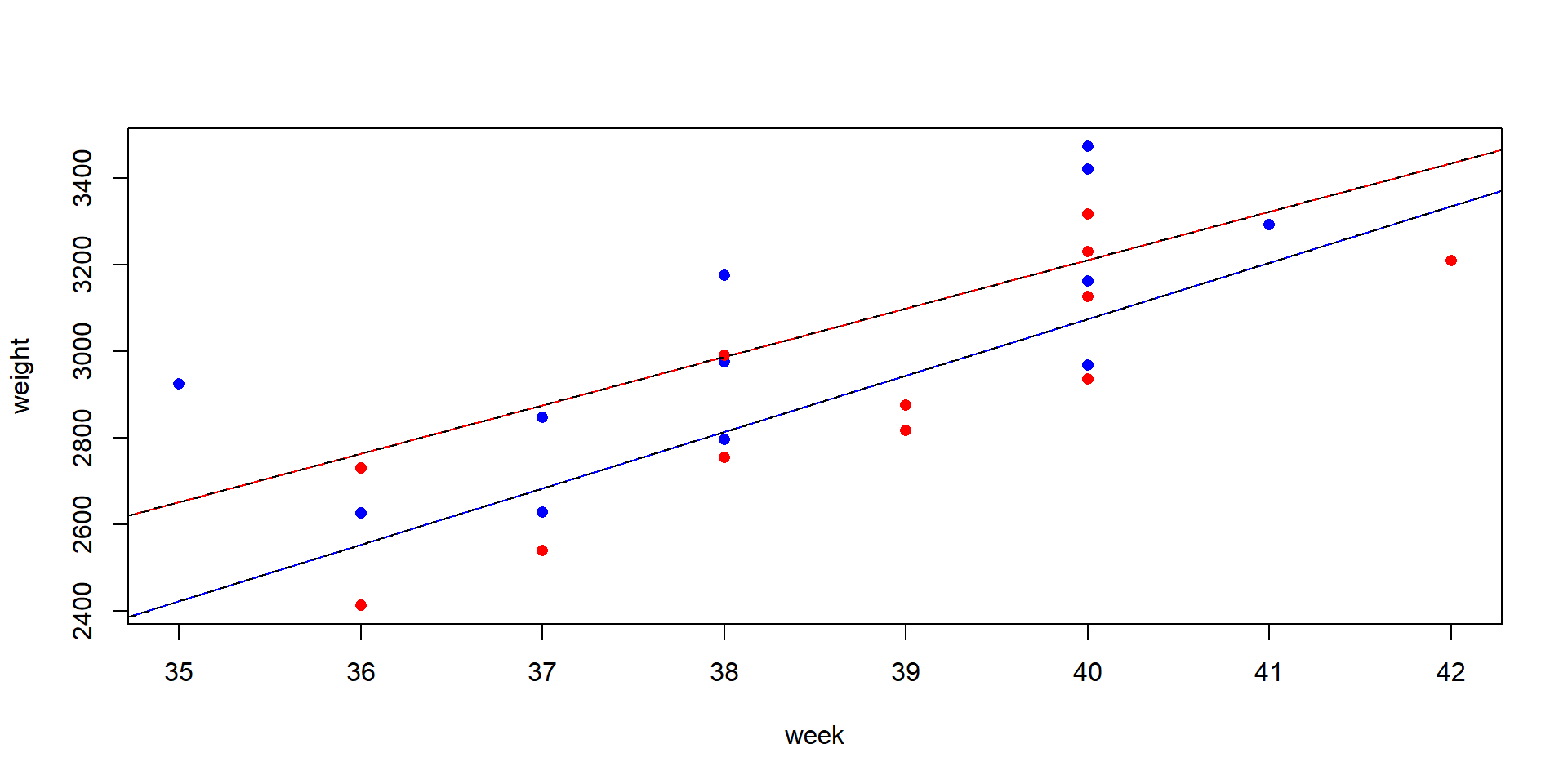

Beispiel: Aus Gründen, die wir später besprechen, muss die Kovariate week als erstes in der Modellformel stehen.

Tücken der ANOVA/ANCOVA

Bisher beschriebene Tücken von ANOVA und ANCOVA

1. Heterogenität der Varianz
   • p-Werte können verzerrt sein (d.h. irreführend oder falsch)
   • Verwendung einer einfachen ANOVA für ungleiche Varianzen (in R: oneway.test)
2. Unbalanzierter Fall
   • Ungleiche Anzahl von Stichproben für jede Faktorkombination
   • \(\rightarrow\) ANOVA-Ergebnisse sind von der Reihenfolge der Faktoren in der Modellformel abhängig.
   • Klassische Lösung: Typ II oder Typ III ANOVA
   • Moderner Ansatz: Modellselektion und Likelihood-Ratio-Tests

Typ II und Typ III ANOVA

• Funktion Anova (mit Großbuchstabe A) im Paket car
• Hilfeseite der Funktion Anova:

Type-II tests are calculated according to the principle of marginality, testing each term after all others, except ignoring the term’s higher-order relatives; so-called type-III tests violate marginality, testing each term in the model after all of the others.

• Schlussfolgerung: Verwende Typ II und nicht Typ III.
• Interpretiere keine einzelnen Haupteffekte, wenn eine signifikante Wechselwirkung vorliegt.

Typ II ANOVA: Beispiel

library("car")
m <- lm(growth ~ light * fert, data = plants)
Anova(m, type="II")

Anova Table (Type II tests)

Response: growth
            Sum Sq Df F value  Pr(>F)  
light      2.61333  1  7.2258 0.03614 *
fert       2.66000  2  3.6774 0.09069 .
light:fert 0.68667  2  0.9493 0.43833  
Residuals  2.17000  6                  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Modellselektion -
ein Paradigmenwechsel

Modellkandidaten und Auswahl eines optimalen Modells

Problem:

• Bei komplexen ANOVA-Modellen hängen die p-Werte von der Anzahl (und manchmal von der Reihenfolge) der einbezogenen Faktoren und Wechselwirkungen ab.
• Der H₀-basierte Ansatz wird eventuell verwirrend, z.B. wegen widersprüchlicher p-Werte.

Alternativer Ansatz:

• Modellselektion – nutzt das Prinzip der Parsimonie

Es werden verschiedene Modellkandidaten verglichen:

• Modell mit allen potentiellen Effekten → vollständiges Modell
• Weglassen einzelner Faktoren → reduzierte Modelle (mehrere!)
• Keine Einflussfaktoren (nur Mittelwert) → Nullmodell
• Welches Modell ist das beste? → minimales adäquates Modell

Wie können wir messen, welches Modell das beste ist?

Kompromiss zwischen Modellanpassung und Modellkomplexität (Anzahl der Parameter, k).

• Güte der Anpassung: Likelihood L – wie gut die Daten zu einem bestimmten Modell passen.
• Log Likelihood: macht das Kriterium additiv.
• AIC (Akaike Information Criterion):

\[AIC = −2 \ln(L) + 2k\]

• BIC ( Bayesian Information Criterion), berücksichtigt den Stichprobenumfang (\(n\)):

\[BIC = −2 \ln(L) + k \cdot \ln(n)\]

Das Modell mit dem kleinsten AIC (oder BIC) ist das minimal adäquate Modell.

Modellselektion und Likelihood-Ratio-Tests

Ansatz

1. Mehrere Modelle einzeln anpassen
2. Modelle paarweise mit ANOVA (Likelihood Ratio Test) vergleichen

Daten und Beispiel

plants <- data.frame(No=1:12,
                   growth=c(6.6, 7.2, 6.9, 8.3, 7.9, 9.2,
                            8.3, 8.7, 8.1, 8.5, 9.1, 9.0),
                   fert= rep(c("A", "B", "C"), each=2),
                   light= rep(c("low", "high"), each=6)
                   )

m3 <- lm(growth ~ fert * light, data=plants)  # f1 + f2 + f1:f2
m2 <- lm(growth ~ fert + light, data=plants)  # f1 + f2
anova(m3, m2)

Analysis of Variance Table

Model 1: growth ~ fert * light
Model 2: growth ~ fert + light
  Res.Df    RSS Df Sum of Sq      F Pr(>F)
1      6 2.1700                           
2      8 2.8567 -2  -0.68667 0.9493 0.4383

• Likelihood-Ratio-Test vergleicht zwei Modelle (anova in R mit > 1 Modell)
• Modell mit Interaktion (m3) nicht signifikant besser als Modell ohne Interaktion (m2).

AIC-basierte Modellselektion

• Der paarweise Modellvergleich ist umständlich, insbesondere bei einer großen Anzahl von Modellen.
• Lösung: Erstelle eine Menge von Kandidatenmodellen
• Verwende kleinstes AIC, um das minimal angemessene Modell auszuwählen.

m3  <- lm(growth ~ light * fert, data = plants) # Gesamtmodell
m2  <- lm(growth ~ light + fert, data = plants)
m1a <- lm(growth ~ fert, data = plants)
m1b <- lm(growth ~ light, data = plants)
m0  <- lm(growth ~ 1, data = plants)            # Nullmodell

AIC(m0, m1a, m1b, m2, m3)

    df      AIC
m0   2 33.38238
m1a  4 32.62699
m1b  3 30.72893
m2   5 26.83151
m3   7 27.53237

Anmerkungen

• AIC-Werte sind bis zu einer additiven Konstante definiert
• \(\rightarrow\) Absolute Werte können je nach Software oder Methode variieren.
• \(\Rightarrow\) Betrachte die Differenzen, nicht die absoluten Werte.
• Faustregel: die „AIC-Einheit“ ist 2, Unterschiede \(\approx\) 2.0 \(\rightarrow\) geringe Bedeutung

Schrittweise Modellselektion (automatisch)

Automatische Modellselektion

m1 <- lm(growth ~ fert * light, data=plants)
opt <- step(m1)

Start:  AIC=-8.52
growth ~ fert * light

             Df Sum of Sq    RSS     AIC
- fert:light  2   0.68667 2.8567 -9.2230
<none>                    2.1700 -8.5222

Step:  AIC=-9.22
growth ~ fert + light

        Df Sum of Sq    RSS     AIC
<none>               2.8567 -9.2230
- fert   2    2.6600 5.5167 -5.3256
- light  1    2.6133 5.4700 -3.4275

Modell mit dem kleinsten AIC \(\rightarrow\) optimales Modell.

Zum Vergleich: klassische ANOVA

anova(opt)

Analysis of Variance Table

Response: growth
          Df Sum Sq Mean Sq F value  Pr(>F)  
fert       2 2.6600 1.33000  3.7246 0.07190 .
light      1 2.6133 2.61333  7.3186 0.02685 *
Residuals  8 2.8567 0.35708                  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Ergebnisse des Beispiels:

• optimales Modell (opt), enthält beide Faktoren (fert, light), aber keine Interaktion.
• Die Modellselektion identifiziert fert und light als wichtige Erklärungsvariablen.
• im Gegensatz zur klassischen ANOVA-Tabelle, in der nur light signifikant war, zeigt die Modellselektion, dass auch fert zur Erklärung beiträgt.

Signifikanztests vs. Modellselektion

• Das Konzept der Modellselektion ersetzt die p-Wert-basierte Statistik, zumindest teilweise.
• Einige Autoren raten davon ab, p-Werte in diesem Kontext noch zu verwenden.
• Andere empfehlen einen Kompromiss: p-Werte als Hilfsmittel, nicht als Entscheidungskriterium.

Derzeitige Empfehlung

Wenn p-Werte benötigt werden, vergleiche das optimale Modell mit reduzierten Modellen:

anova(m2, m1a) # fert
anova(m2, m1b) # light

• Interpretiere p-Werte mit Vorsicht:
  • Sie sind abhängig von der Modellstruktur.
  • Sie können irreführend sein, wenn das Modell nicht optimal ist.
• Gib auch Effektstärken und Vertrauensintervalle an!

Zusammenfassung des Kapitels ANOVA

• Lineare Modelle bilden die Grundlage für viele statistische Methoden
  • Lineare Regression
  • ANOVA/ANCOVA anstelle von Mehrfachtests
  • MANOVA, GLM, GAM, GLMM, . . .
• ANOVA ist leistungsfähiger als Mehrfachtests:
  • vermeidet \(\alpha\)-Fehlerinflation
  • identifiziert Interaktionseffekte
  • eliminiert Kovariate
  • ein großes Experiment benötigt weniger Stichprobengröße als viele kleine Experimente
• Modellselektion vs. p-Wert-basierte Tests
  • Paradigmenwechsel: AIC anstelle von p-Werten
  • zuverlässiger, besonders bei unausgewogenen oder komplexen Designs
  • erweiterbar auf GLM, GAM, LME, GLMM, …
  • aber: p-Wert-basierte Tests sind manchmal leichter zu verstehen

Selbststudium: Lies das Paper von Johnson & Omland (2004) zum Thema Modellselektion.

Vermeide Manipulation von p-Werten

Experimente NICHT wiederholen, bis ein signifikanter p-Wert gefunden wird!

Leek et al. (2017) in Nature:

“… Nature asked influential statisticians to recommend one change to improve science. The common theme? The problem is not our maths, but ourselves.”:

Five ways to fix statistics. Comment on Nature

1. Jeff Leek: Adjust for human cognition
2. Blakeley B. McShane & Andrew Gelman: Abandon statistical significance
3. David Colquhoun: State false-positive risk, too
4. Michèle B. Nuijten: Share analysis plans and results
5. Steven N. Goodman: Change norms from within

The “ASA Statement …”

Das ASA Statement on Statistical Significance and P-Values der American Statistical Association (Wasserstein & Lazar, 2016) befasst sich mit der Bedeutung des p-Werts, ohne ihn komplett in Frage zu stellen. Es definiert 6 Prinzipien:

1. P-values can indicate how incompatible the data are with a specified statistical model.
2. P-values do not measure the probability that the studied hypothesis is true, or the probability that the data were produced by random chance alone.
3. Scientific conclusions and business or policy decisions should not be based only on whether a p-value passes a specific threshold.
4. Proper inference requires full reporting and transparency.
5. A p-value, or statistical significance, does not measure the size of an effect or the importance of a result.
6. By itself, a p-value does not provide a good measure of evidence regarding a model or hypothesis.

Die Details sind im Statement weiter ausgeführt.

Selbststudium: Lies dazu neben Wasserstein & Lazar (2016) auch Hurlbert et al. (2019).

Literaturverzeichnis

Crawley, M. J. (2002). Statistical computing. An introduction to data analysis using S-PLUS (pp. 1–761). Wiley. datasets: http://www.bio.ic.ac.uk/research/mjcraw/statcomp/data/

Dobson, A. J. (2013). Introduction to statistical modelling. Springer.

Dziallas, C., & Grossart, H.-P. (2011). Increasing Oxygen Radicals and Water Temperature Select for Toxic Microcystis sp. PLoS ONE, 6(9), e25569. https://doi.org/10.1371/journal.pone.0025569

Holm, S. (1979). A simple sequentially rejective multiple test procedure. Scandinavian Journal of Statistics, 65–70. https://www.jstor.org/stable/4615733

Hurlbert, S. H., Levine, R. A., & Utts, J. (2019). Coup de Grâce for a tough old bull: “Statistically Significant” expires. The American Statistician, 73(sup1), 352–357. https://doi.org/10.1080/00031305.2018.1543616

Jähnichen, S., Ihle, T., Petzoldt, T., & Benndorf, J. (2007). Impact of Inorganic Carbon Availability on Microcystin Production by Microcystis aeruginosa PCC 7806. Applied and Environmental Microbiology, 73(21), 6994–7002. https://doi.org/10.1128/AEM.01253-07

Jähnichen, S., Long, B. M., & Petzoldt, T. (2011). Microcystin production by Microcystis aeruginosa: Direct regulation by multiple environmental factors. Harmful Algae, 12, 95–104. https://doi.org/10.1016/j.hal.2011.09.002

Jähnichen, S., Petzoldt, T., & Benndorf, J. (2001). Evidence for control of microcystin dynamics in Bautzen Reservoir (Germany) by cyanobacterial population growth rates and dissolved inorganic carbon. Fundamental and Applied Limnology, 150(2), 177–196. https://doi.org/10.1127/archiv-hydrobiol/150/2001/177

Johnson, G., Jerald, & Omland, K. S. (2004). Model Selection in Ecology and Evolution. Trends in Ecology and Evolution, 19(2), 101–108. https://doi.org/10.1016/j.tree.2003.10.013

Leek, J., McShane, B. B., Gelman, A., Colquhoun, D., Nuijten, M. B., & Goodman, S. N. (2017). Five ways to fix statistics. Nature, 551(7682), 557–559. https://doi.org/10.1038/d41586-017-07522-z

Wasserstein, R. L., & Lazar, N. A. (2016). The ASA Statement on p-values: Context, process, and purpose. The American Statistician, 70(2), 129–133. https://doi.org/10.1080/00031305.2016.1154108

Wei, N., Hu, C., Dittmann, E., Song, L., & Gan, N. (2024). The biological functions of microcystins. Water Research, 262, 122119. https://doi.org/https://doi.org/10.1016/j.watres.2024.122119

Zilliges, Y., Kehr, J.-C., Meissner, S., Ishida, K., Mikkat, S., Hagemann, M., Kaplan, A., Börner, T., & Dittmann, E. (2011). The Cyanobacterial Hepatotoxin Microcystin Binds to Proteins and Increases the Fitness of Microcystis under Oxidative Stress Conditions. PLoS ONE, 6(3), e17615. https://doi.org/10.1371/journal.pone.0017615