06-Lineare Regression
Angewandte Statistik – Ein Praxiskurs
2025-12-13
Lineare Regression
Das lineare Modell
\[ y_i = \alpha + \beta_1 x_{i,1} + \beta_2 x_{i,2} + \cdots + \beta_p x_{i,p} + \varepsilon_i \]
Grundlage vieler statistischer Verfahren
- Lineare Regression einschließlich einiger (auf den ersten Blick) „nichtlinearer“ Funktionen
- Tests für zwei oder mehr Stichproben oder Faktoren: ANOVA, ANCOVA, GLM…
- Multivariate Statistik (z. B. PCA)
- Zeitreihenanalyse (z. B. ARIMA)
- Imputation (Schätzung von fehlenden Werten)
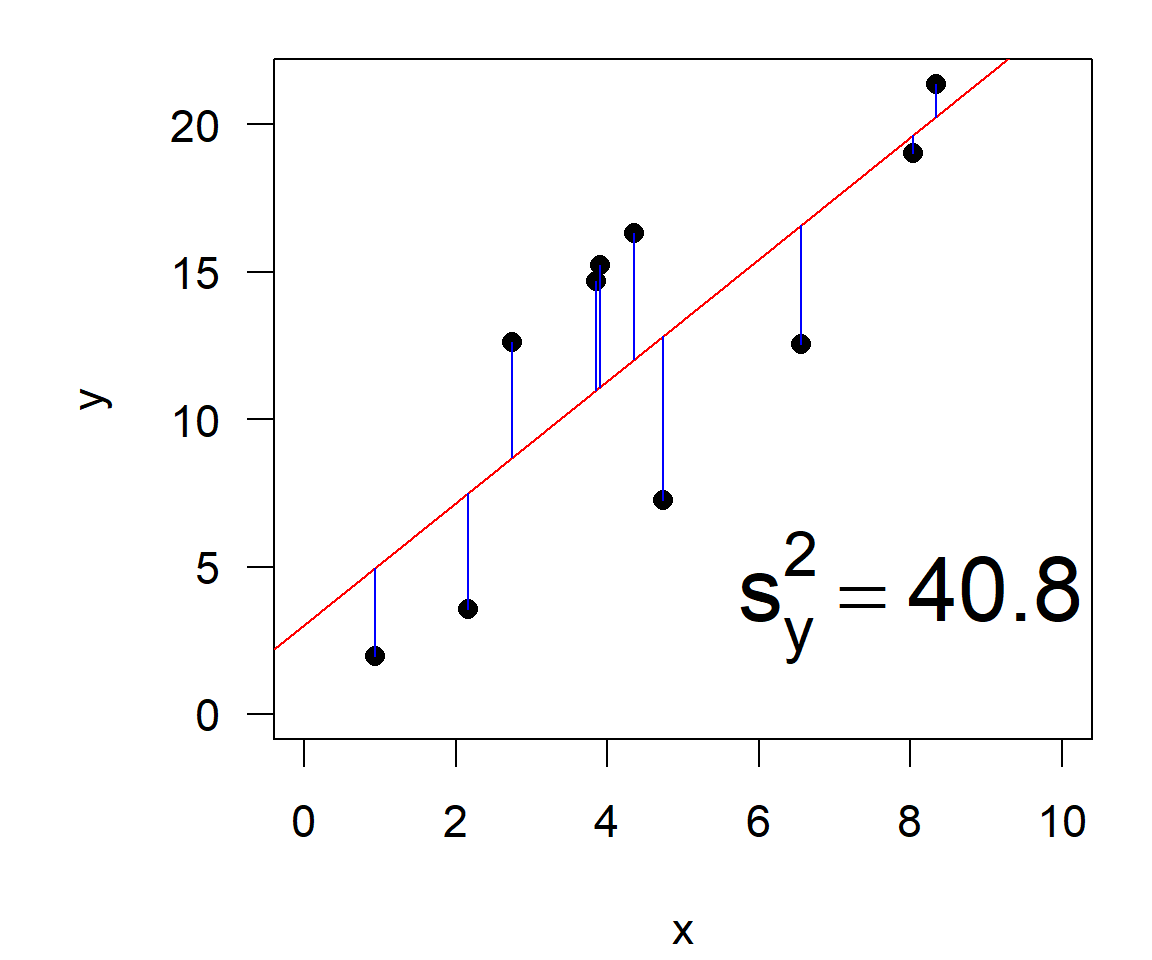
Methode der kleinsten Quadrate
\[ RSS = \sum_{i=1}^n (y_i - \hat{y}_i)^2 = \sum_{i=1}^n \varepsilon^2 \qquad \text{(residual sum of squares)} \]
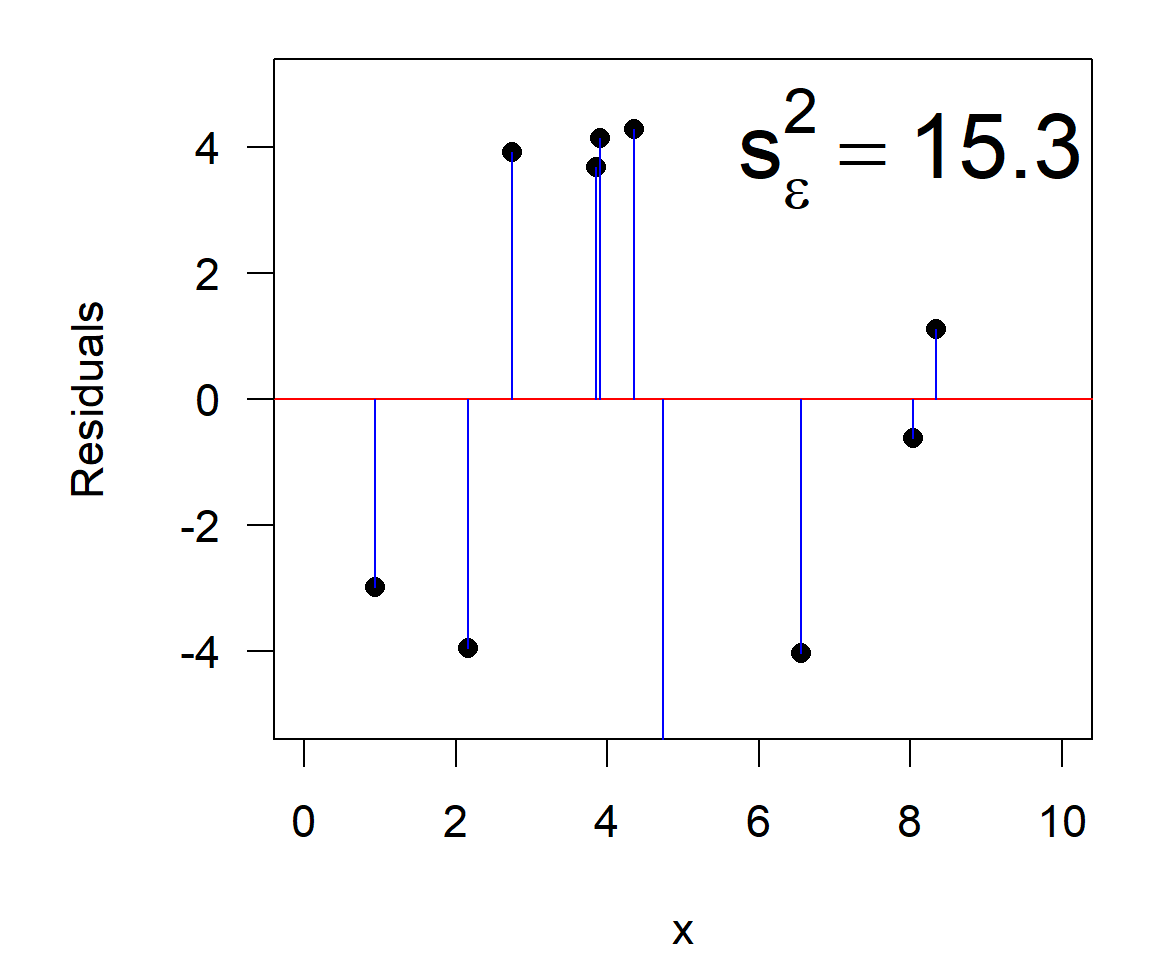
\[\begin{align} \text{Gesamtvarianz} &= \text{erklärte Varianz} & + & \text{Restvarianz}\\ ^2_y &= s^2_{y|x} & + & s^2_{\varepsilon} \end{align}\]
Das Bestimmtheitsmaß
\[\begin{align} r^2 & = \frac{\text{erklärte Varianz}}{\text{Gesamtvarianz}}\\ & = \frac{s^2_{y|x}}{s^2_y}\\ \end{align}\]
… kann als Verhältnis zwischen der Summe der Residuenquadrate (RSS) und der Gesamtsumme (TSS = total sum of squares) ausgedrückt werden:
\[ r^2 = 1-\frac{s^2_{\varepsilon}}{s^2_{y}} = 1-\frac{RSS}{TSS} = 1- \frac{\sum(y_i -\hat{y}_i)^2}{\sum(y_i - \bar{y})^2} \]
- „Summe der Quadrate“, skaliert als relative Varianz
- identisch mit der quadrierten Pearson-Korrelation \(r^2\) (im linearen Fall)
- Sehr nützliche Interpretation:
\(\rightarrow\) Prozentsatz der Varianz der Rohdaten, der durch das Modell erklärt wird.
Im Beispiel: \(r^2 = 1-\) 15.3 \(/\) 40.8 \(=\) 0.625
Analytische Lösung
- Minimierung der Summe der Quadrate (\(\sum \varepsilon^2\))
- Minimale RSS \(\longleftarrow\) partielle 1. Ableitungen aller Parameter (\(\partial p = 0\))
- Lineares Gleichungssystem
Für \(y=a \cdot x + b\) mit 2 Parametern: \(\frac{\partial\sum \varepsilon^2}{\partial{a}}=0\), \(\frac{\partial\sum \varepsilon^2}{\partial{b}}=0\):
\[\begin{align} \frac{\partial \sum(\hat{y_i} - y_i)^2}{\partial a} &= \frac{\partial \sum(a + b \cdot x_i - y_i)^2}{\partial a} = 0\\ \frac{\partial \sum(\hat{y_i} - y_i)^2}{\partial b} &= \frac{\partial \sum(a + b \cdot x_i - y_i)^2}{\partial b} = 0 \end{align}\]
Lösung des linearen Gleichungssystems:
\[ b =\frac {\sum x_iy_i - \frac{1}{n}(\sum x_i \sum y_i)} {\sum x_i^2 - \frac{1}{n}(\sum x_i)^2}, \quad a =\frac {\sum y_i - b \sum x_i}{n} \]
- Lösung für eine beliebige Anzahl von Parametern mit Matrixalgebra.
Signifikanz der Regression
\[
\hat{F}_{1;n-2;\alpha}= \frac{s^2_{explained}}{s^2_{residual}}
= \frac{r^2(n-2)}{1-r^2}
\]
Annahmen
- Gültigkeit: die Daten entsprechen der Forschungsfrage
- Additivität und Linearität: \(y = \alpha + \beta_1 x_1 + \beta_2 x_2 + \cdots\)
- Unabhängigkeit der Fehler: Residuen um die Regressionslinie sind unabhängig
- Gleiche Varianz der Fehler: Residuen sind homogen um die Regressionsgerade verteilt
- Normalität der Fehler: die „Annahme, die im Allgemeinen am wenigsten wichtig ist“
Siehe: Gelman & Hill (2007) : Data analysis using regression …
Diagnostik
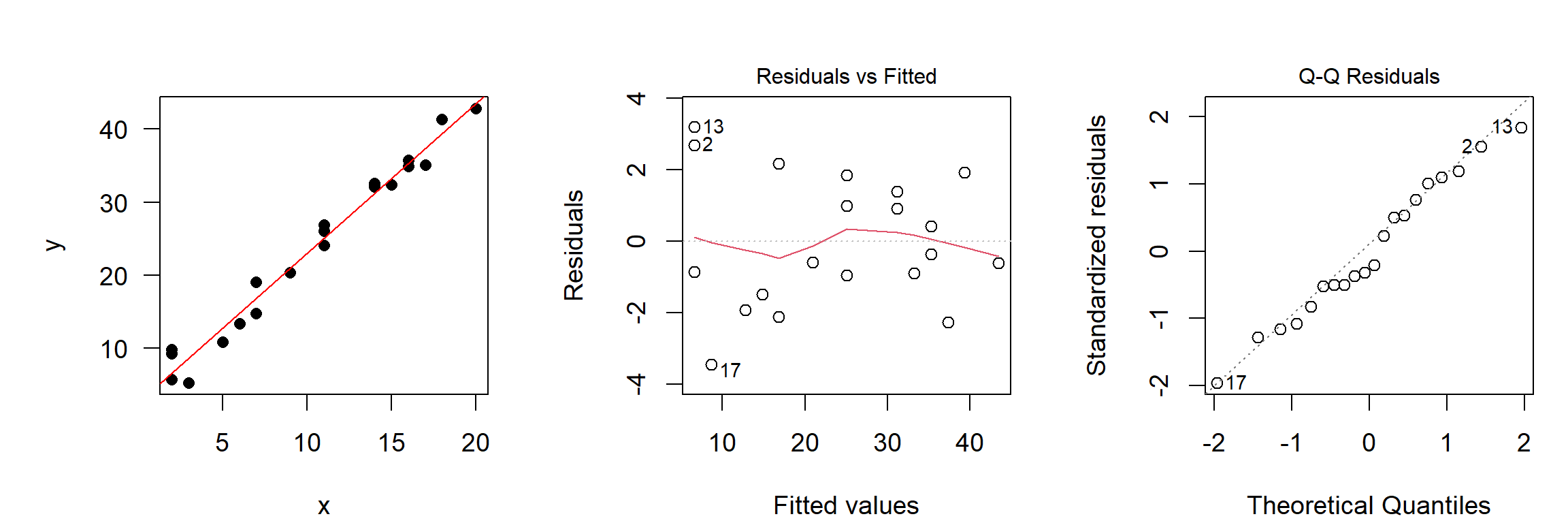
Keine Regressionsanalyse ohne grafische Diagnostik!
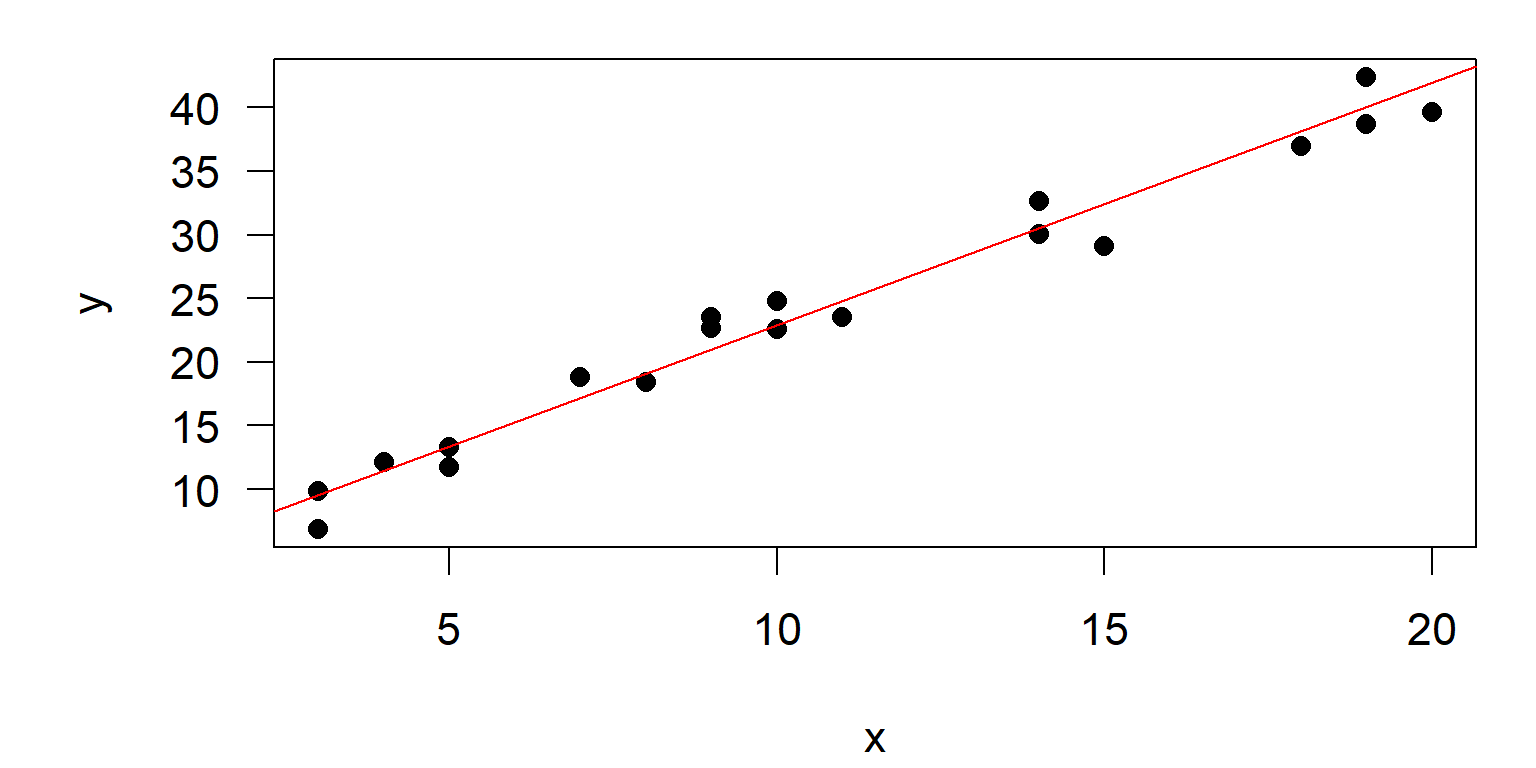
- x-y-Plot mit Regressionsgerade: ist die Varianz homogen?
- Plot der Residuen vs. gefittet: gibt es noch irgendwelche Restmuster?
- Q-Q- Plot, Histogramm: Ist die Verteilung der Residuen näherungsweise normal?
Prüfe annähernde Normalität grafisch, vertraue nicht auf Shapiro-Wilks.
Konfidenzintervalle der Parameter
- Basierend auf Standardfehlern und t-Verteilung, ähnlich wie beim CI des Mittelwerts
\[\begin{align} a & \pm t_{1-\alpha/2, n-2} \cdot s_a\\ b & \pm t_{1-\alpha/2, n-2} \cdot s_b \end{align}\]
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-3.4451 -1.0894 -0.4784 1.5065 3.1933
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.50740 0.87338 2.871 0.0102 *
x 2.04890 0.07427 27.589 3.51e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.885 on 18 degrees of freedom
Multiple R-squared: 0.9769, Adjusted R-squared: 0.9756
F-statistic: 761.1 on 1 and 18 DF, p-value: 3.514e-16
Beispiel: CI von a: \(a \pm t_{1-\alpha/2, n-2} \cdot s_a = 2.5074 \pm
2.09 \cdot 0.87338\)
Konfidenzintervall und Vorhersageintervall
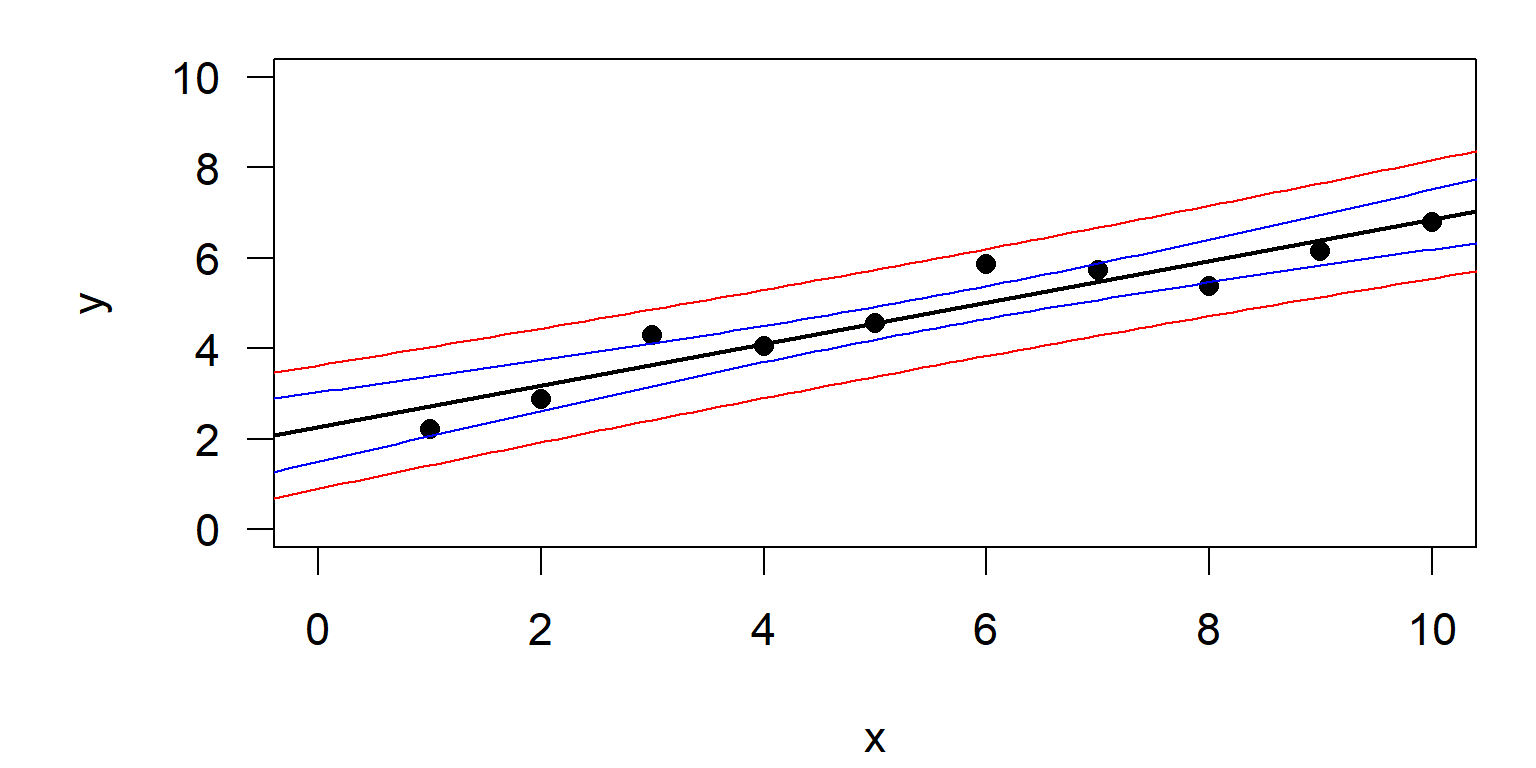
- Konfidenzintervall:
- Zeigt den Bereich, in dem die „wahre Regressionslinie“ zu 95 % erwartet wird.
- Die Breite dieses Bereichs nimmt mit zunehmendem \(n\) ab.
- analog zum Standardfehler
- Vorhersageintervall:
- Zeigt den Bereich, in dem die Vorhersage für einen einzelnen Wert (zu 95%) erwartet wird.
- Die Breite ist unabhängig vom Stichprobenumfang \(n\).
- analog zur Standardabweichung
Konfidenzintervalle für die lineare Regression: Code
## generiere Beispiel Daten
x <- 1:10
y <- 2 + 0.5 * x + 0.5 * rnorm(x)
## fitte Modell
reg <- lm(y ~ x)
summary(reg)
## Daten und Regressionslinie plotten
plot(x,y, xlim = c(0, 10), ylim = c(0, 10), pch = 16)
abline(reg, lwd = 2)
## Intervalle berechnen und plotten
newdata <- data.frame(x=seq(-1, 11, length=100))
conflim <- predict(reg, newdata=newdata, interval = "confidence")
predlim <- predict(reg, newdata=newdata, interval = "prediction")
lines(newdata$x, conflim[,2], col = "blue")
lines(newdata$x, conflim[,3], col = "blue")
lines(newdata$x, predlim[,2], col = "red")
lines(newdata$x, predlim[,3], col = "red")- Die Variable
newdata:- überspannt den Bereich der
x-Werte in kleinen Schritten für eine glatte Kurve - hier: eine einzige Spalte mit genau demselben Namen
xwie in der Modellformel - bei multipler Regression: eine Spalte pro Erklärungsvariable
- überspannt den Bereich der
Problemfälle
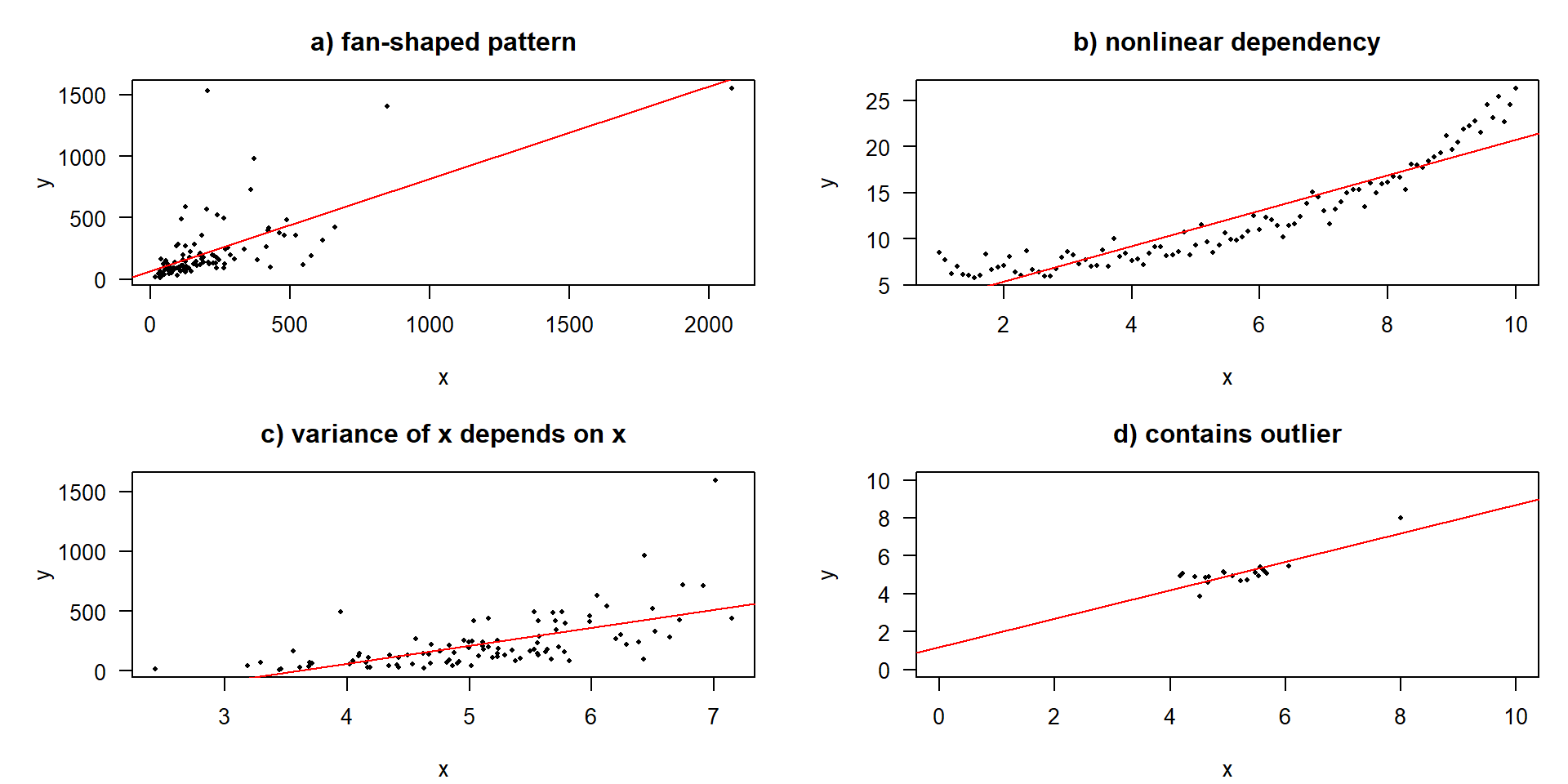
Identifizierung und Behandlung von Problemfällen
Rainbow-Test (Linearität)
Rainbow test
data: y ~ x
Rain = 0.79952, df1 = 5, df2 = 3, p-value = 0.6153Breusch-Pagan-Test (Homogenität der Varianz)
Nicht-Normalität und Ausreißer
- Nicht-Normalität
- weniger wichtig, als viele Leute denken ( aufgrund des CLTs)
- Transformationen (z. B. Box-Cox), Polynome, periodische Funktionen
- Verwendung von GLM’s (generalized linear models)
- Ausreißer (abhängig vom Muster)
- Verwendung von Transformationen (z.B. Doppellog)
- Verwendung von Ausreißer-Tests, z.B.
outlierTestaus Paket car - robuste Regression mit IWLS aus dem Paket MASS
Robuste Regression mit IWLS
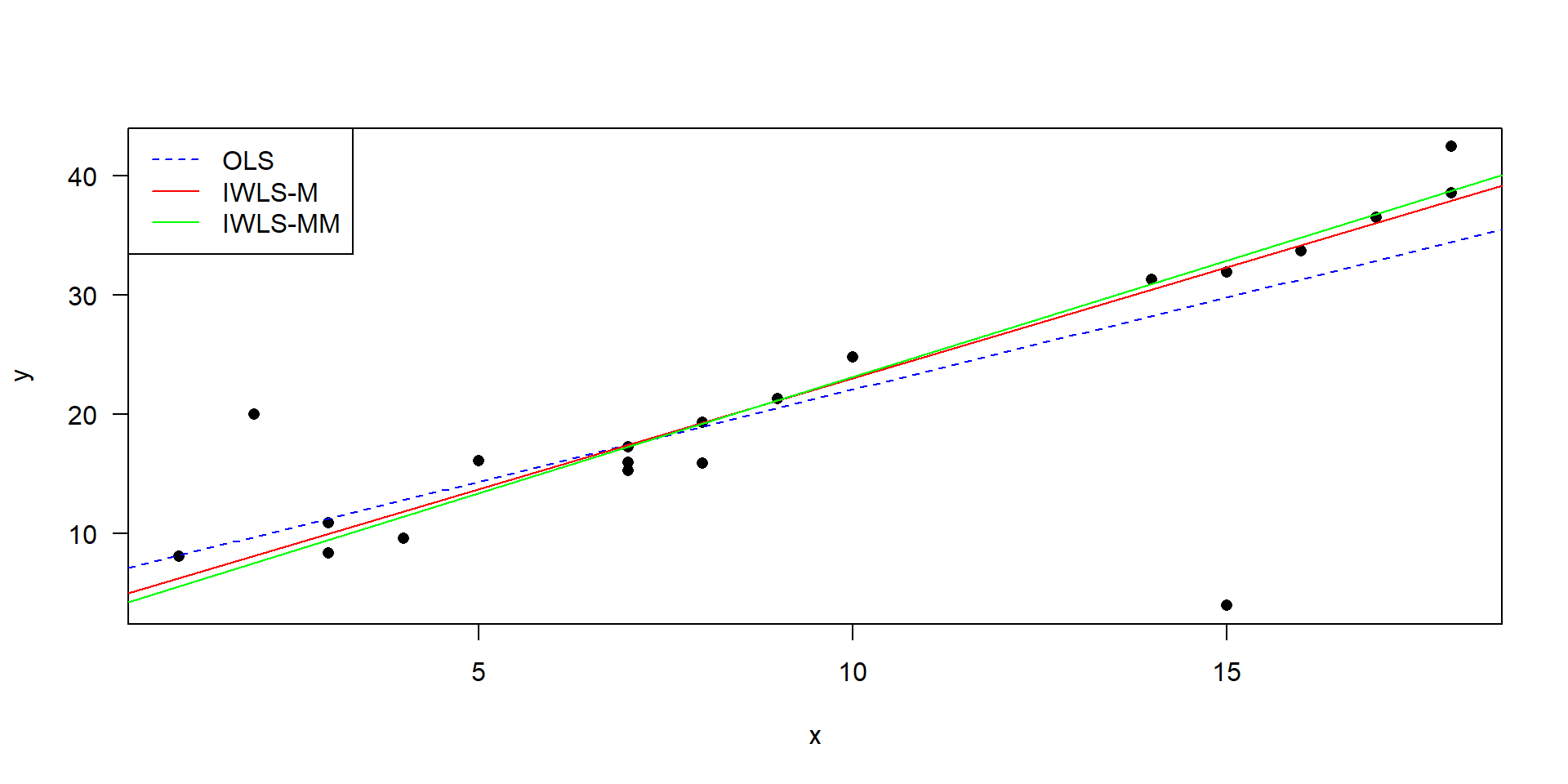
- OLS (gewöhnliche kleinste Quadrate, engl. ordinary least squares) ist die „normale“ Regression.
- IWLS: iterated re-weighted least squares
- M- bzw. MM-Schätzung: zwei verschiedene Ansätze, Details in Venables & Ripley (2013)
- robuste Regression ist dem Ausschluss von Ausreißern vorzuziehen
Code der IWLS-Regression
library("MASS")
## Testdaten mit 2 „Ausreißern“
x <- c(1, 2, 3, 3, 4, 5, 7, 7, 7, 8, 8, 9, 10, 14, 15, 15, 16, 17, 18, 18)
y <- c(8.1, 20, 10.9, 8.4, 9.6, 16.1, 17.3, 15.3, 16, 15.9, 19.3,
21.3, 24.8, 31.3, 4, 31.9, 33.7, 36.5, 42.4, 38.5)
## Fitten der Modelle
ssq <- lm(y ~ x)
iwls <- rlm(y ~ x)
iwlsmm <- rlm(y ~ x, method = "MM")
## Plotten der Modelle
plot(x, y, pch = 16, las = 1)
abline(ssq, col = "blue", lty = "dashed")
abline(iwls, col = "red")
abline(iwlsmm, col = "green")
legend("topleft", c("OLS", "IWLS-M", "IWLS-MM"),
col = c("blue", "red", "green"),
lty = c("dashed", "solid", "solid"))Weiterführende Literatur
- Kleiber & Zeileis (2008) Applied econometrics with R. Springer Verlag.
- Venables & Ripley (2013) Modern applied statistics with S-PLUS (3rd ed.). Springer Science & Business Media.
- Fox & Weisberg (2018) An R companion to applied regression. Sage publications.
- Gelman & Hill (2007) Data analysis using regression and multilevel hierarchical models (Vol. 1). Cambridge University Press, New York.