5.5 + c(-1, 1) * qt(0.975, 10-1) * 1/sqrt(10)[1] 4.784643 6.215357Angewandte Statistik – Ein Praxiskurs
2025-12-13
Ein statistischer Test hilft zu entscheiden, ob eine Hypothese wahrscheinlich richtig ist oder nicht, basierend auf vorliegenden Daten.
siehe dazu auch: https://de.wikipedia.org/wiki/Statistischer_Test
Für Mittelwertdifferenzen ist die relative Effektstärke:
\[ \delta = \frac{\bar{\mu}_1-\bar{\mu}_2}{\sigma}=\frac{\Delta}{\sigma} \]
mit:
\(H_0\) Nullhypothese: Zwei Grundgesamtheiten unterscheiden sich nicht in Bezug auf eine bestimmte Eigenschaft.
\(H_a\) Alternativhypothese (Versuchshypothese): Vorhandensein eines bestimmten Effekts.
„Nicht signifikant“ bedeutet entweder kein Effekt oder Stichprobengröße zu klein!
Anmerkung: Unterschiedliche Bedeutung von Signifikanz (\(H_0\) unwahrscheinlich) und Relevanz (Effekt groß genug, um in der Praxis eine Rolle zu spielen).
Die Interpretation des p-Wertes war in der Vergangenheit oft verwirrend, selbst in Statistik-Lehrbüchern, so dass es gut ist, sich auf eine klare Definition zu beziehen:
Der p-Wert ist definiert als die Wahrscheinlichkeit, ein Ergebnis zu erhalten, das gleich oder „extremer“ ist als das, was tatsächlich beobachtet wurde, wenn die Nullhypothese wahr ist.
Hubbard (2004) Alphabet Soup: Blurring the Distinctions Between p’s and a’s in Psychological Research, Theory Psychology 14(3), 295-327. DOI: 10.1177/0959354304043638
| Realität | Entscheidung des Tests | Richtig? | Wahrscheinlichkeit |
|---|---|---|---|
| \(H_0\) = wahr | signifikant | nein | \(\alpha\)-Fehler |
| \(H_0\) = falsch | nicht signifikant | nein | \(\beta\)-Fehler |
| \(H_0\) = wahr | nicht signifikant | ja | \(1-\alpha\) |
| \(H_0\) = falsch | signifikant | ja | \(1-\beta\) (Trennschärfe) |
1.\(H_0\) fälschlicherweise abgelehnt (Fehler erster Art oder \(\alpha\)-Fehler)
2.\(H_0\) fälschlicherweise beibehalten (Fehler zweiter Art oder \(\beta\)-Fehler)
Verwendung in der Praxis
Statistische Signifikanz: die Nullhypothese \(H_0\) ist im statistischen Sinne unwahrscheinlich.
Praktische Relevanz (manchmal auch „praktische Signifikanz“ genannt): die Effektstärke ist groß genug, um in der Praxis eine Rolle zu spielen.
Ob ein Effekt relevant sein kann oder nicht, hängt also von seiner Effektstärke und dem Anwendungsbereich ab.
Betrachten wir zum Beispiel eine Impfung. Wenn ein Impfstoff in einem klinischen Test eine signifikante Wirkung hat, aber nur 10 von 1000 Menschen schützt, würde man diesen Effekt nicht als relevant ansehen und diesen Impfstoff nicht herstellen.
Andererseits können auch kleine Wirkungen von Bedeutung sein. Wenn also eine toxische Substanz bei 1 von 1000 Personen Krebs auslösen würde, würden wir das als relevant betrachten. Um es auch als signifikant zu erkennen, ist eine epidemiologische Studie mit einer großen Anzahl von Menschen erforderlich. Da es sich aber um eine hochrelevante Wirkung handelt, lohnt sich der Aufwand.
Ein p-Wert misst die Wahrscheinlichkeit, dass ein rein zufälliger Effekt gleich groß oder größer ist als ein beobachteter Effekt, wenn die Nullhypothese wahr ist.
Signifikant, die Ergebnisse sind unwahrscheinlich, wenn es keinen echten Effekt gäbe.
Nicht signifikant bedeutet nicht „kein Effekt“.
Nicht signifikante Ergebnisse deuten auf die Notwendigkeit weiterer Untersuchungen hin:
Wichtig: Konzentriere Dich nicht nur auf p-Werte und Signifikanz!
Vergiss nie, Stichprobengröße, Effektstärke und Relevanz anzugeben.
Bei großen Datensätzen:
\[ CI = \bar{x} \pm t_{1-\alpha/2, n-1} \cdot s_{\bar{x}} \] mit \[ s_{\bar{x}} = \frac{s}{\sqrt{n}} \qquad \text{(Standardfehler)} \]
Auf den folgenden Folien werden unterschiedliche Berechnungsmethoden vorgestellt.
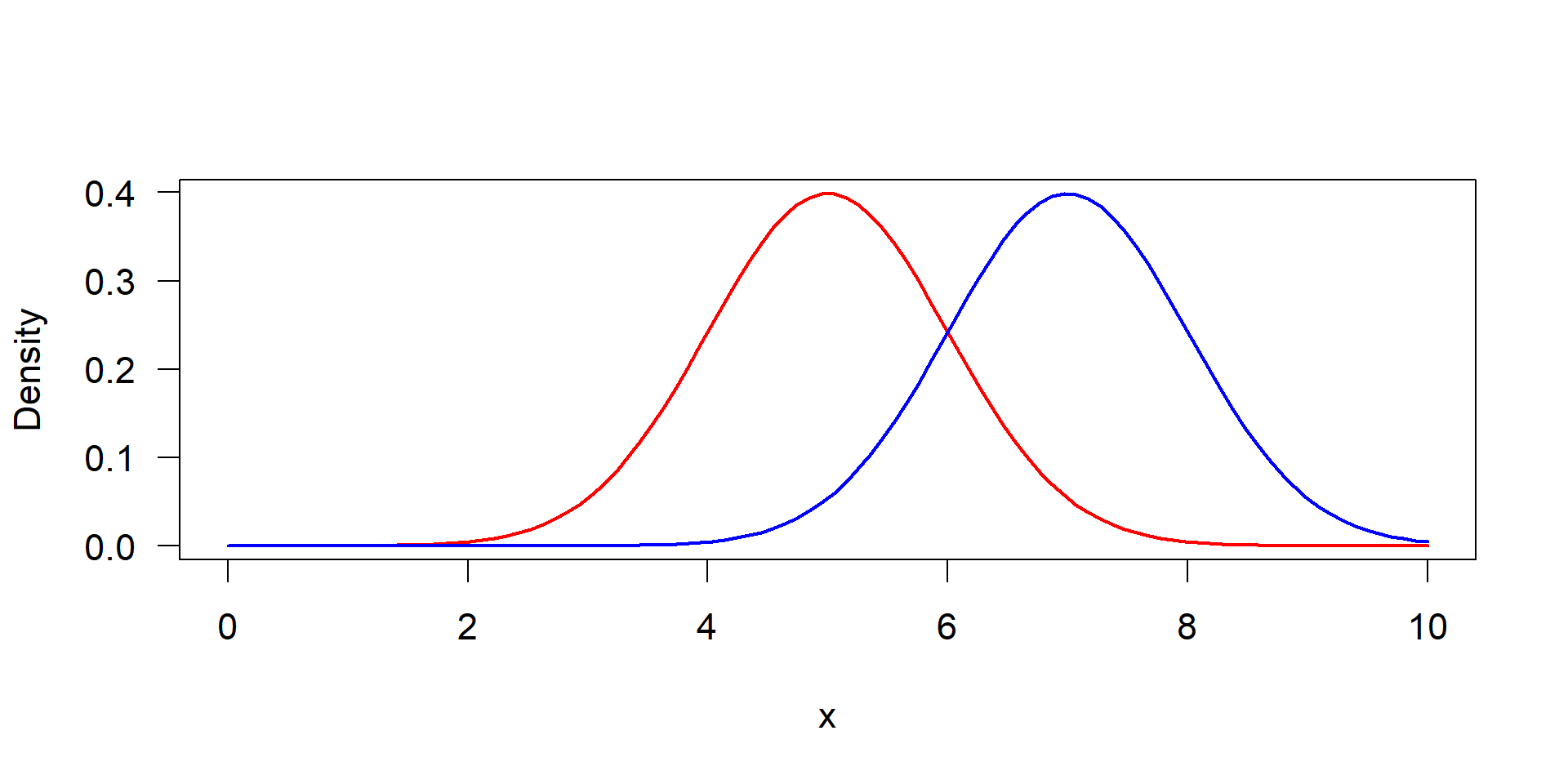
Visualisierung eines Einstichproben-t-Test. Links: ursprüngliche Verteilung der Daten, gemessen an der Standardabweichung, rechts: Verteilung der Mittelwerte, gemessen an ihrem Standardfehler.
\[ s_{\bar{x}} = \frac{s}{\sqrt{n}} \qquad \text{(Standardfehler)} \]
Wichtig: Der Test arbeitet mit der Verteilung der Mittelwerte, nicht mit der Verteilung der ursprünglichen Daten.
Stichprobe: \(n=10, \bar{x}=5.5, s=1\) und \(\mu=5\)
Wenn \(\alpha = 0,05\) ist, erhalten wir ein zweiseitiges 95%-Konfidenzintervall mit:
\[\bar{x} \pm t_{0,975, n-1} \cdot \frac{s}{\sqrt{n}}\]
Prüfung, ob \(\mu=5.0\) in diesem Intervall liegt?
Ja, es befindet sich innerhalb \(\Rightarrow\) Unterschied nicht signifikant.
\[ t_{obs} = |\bar{x}-\mu | \cdot \frac{1}{s_{\bar{x}}} = \frac{|\bar{x}-\mu |}{s} \cdot \sqrt{n} = \frac{|5.5 -5.0|}{1.0} \cdot \sqrt{10} \]
Berechnung in R:
Vergleich: \(1.58 < 2.26\) \(\Rightarrow\) kein signifikanter Unterschied zwischen \(\bar{x}\) und \(\mu\).
pt) anstelle des TabellenvergleichsDer p-Wert = 0.1483047 ist größer als \(0,05\), somit betrachten wir die Differenz als nicht signifikant.
FAQ: kleiner oder größer als?
| p-Wert | \(\text{p-Wert} < \alpha\) | Nullhypothese unwahrscheinlich | signifikant |
| Test Statistik | \(t_{obs} > t_{1-\alpha/2, n-1}\) | Effekt übersteigt Grenze | signifikant |
Das Gleiche kann man viel einfacher mit dem Computer in R machen.
Angenommen, wir haben eine Stichprobe mit \(\bar{x}=5, s=1\):
## definiere Stichprobe
x <- c(5.5, 3.5, 5.4, 5.3, 6, 7.2, 5.4, 6.3, 4.5, 5.9)
## führe Einstichproben-t-Test durch
t.test(x, mu = 5)
One Sample t-test
data: x
t = 1.5811, df = 9, p-value = 0.1483
alternative hypothesis: true mean is not equal to 5
95 percent confidence interval:
4.784643 6.215357
sample estimates:
mean of x
5.5 Der Test liefert den beobachteten t-Wert, das 95%-Konfidenzintervall und den p-Wert.
Ein wichtiger Unterschied ist, dass diese Methode mit den Originaldaten arbeitet, während die anderen Methoden nur Mittelwert, Standardabweichung und Stichprobenumfang benötigen.
Der Zweistichproben-t-Test vergleicht zwei unabhängige Stichproben:
x1 <- c(5.3, 6.0, 7.1, 6.4, 5.7, 4.9, 5.0, 4.6, 5.7, 4.0, 4.5, 6.5)
x2 <- c(5.8, 7.1, 5.8, 7.0, 6.7, 7.7, 9.2, 6.0, 7.2, 7.8, 7.8, 5.7)
t.test(x1, x2)
Welch Two Sample t-test
data: x1 and x2
t = -3.7185, df = 21.611, p-value = 0.001224
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-2.3504462 -0.6662205
sample estimates:
mean of x mean of y
5.475000 6.983333 \(H_0\) \(\mu_1 = \mu_2\)
\(H_a\) die beiden Mittelwerte sind unterschiedlich
Testkriterium
\[ t_{obs} =\frac{|\bar{x}_1-\bar{x}_2|}{s_{tot}} \cdot \sqrt{\frac{n_1 n_2}{n_1+n_2}} \]
gepoolte Standardabweichung
\[ s_{tot} = \sqrt{{({n}_1 - 1)\cdot s_1^2 + ({n}_2 - 1)\cdot s_2^2 \over ({n}_1 + {n}_2 - 2)}} \]
Annahmen: Unabhängigkeit, gleiche Varianzen, annähernde Normalverteilung
Bekannt als t-Test für Stichproben mit ungleicher Varianz, funktioniert auch bei gleicher Varianz!
Testkriterium:
\[ t = \frac{\bar{x}_1 - \bar{x}_2}{\sqrt{s^2_{\bar{x}_1} + s^2_{\bar{x}_2}}} \]
Standardfehler der einzelnen Stichproben:
\[ s_{\bar{x}_i} = \frac{s_i}{\sqrt{n_i}} \] Korrigierte Freiheitsgrade:
\[ \text{df} = \frac{\frac{s^2_1}{n_1} + \frac{s^2_2}{n_2}}{\frac{s^4_1}{n^2_1(n_1-1)} + \frac{s^4_2}{n^2_2(n_2-1)}} \]
… das ist die Standardmethode der t.test-Funktion.
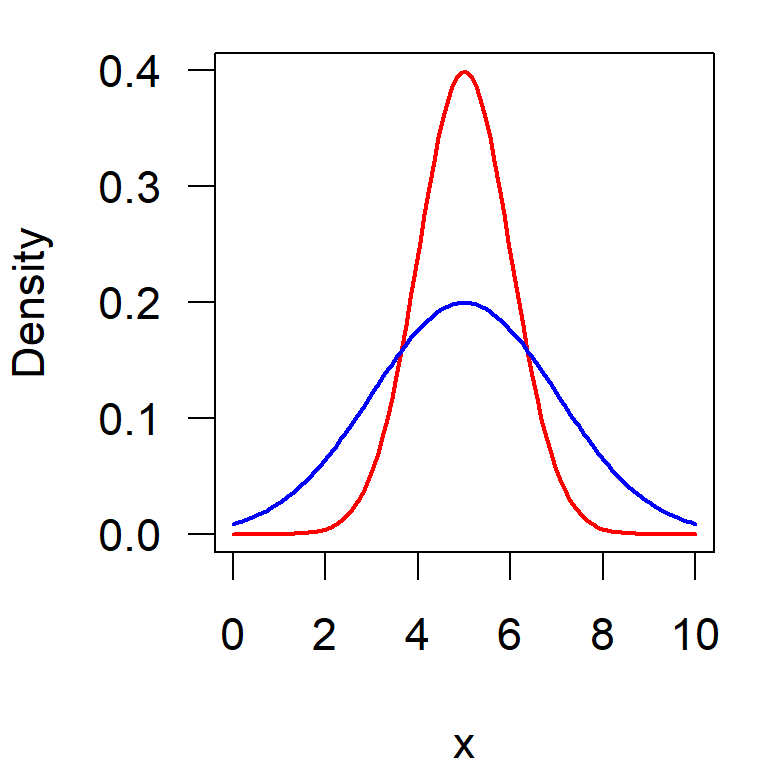
\(H_0\): \(\sigma_1^2 = \sigma_2^2\)
\(H_a\): Varianzen ungleich
Testkriterium:
\[F = \frac{s_1^2}{s_2^2} \]
Beispiel:
\(\Rightarrow\) \(F_{9, 4, \alpha=0.975} = 8.9 > 4 \quad\rightarrow\) nicht signifikant
Bartlett’s Test:
Bartlett test of homogeneity of variances
data: list(x1, x2, x3)
Bartlett's K-squared = 7.7136, df = 2, p-value = 0.02114
Fligner-Killeen Test (empfohlen):
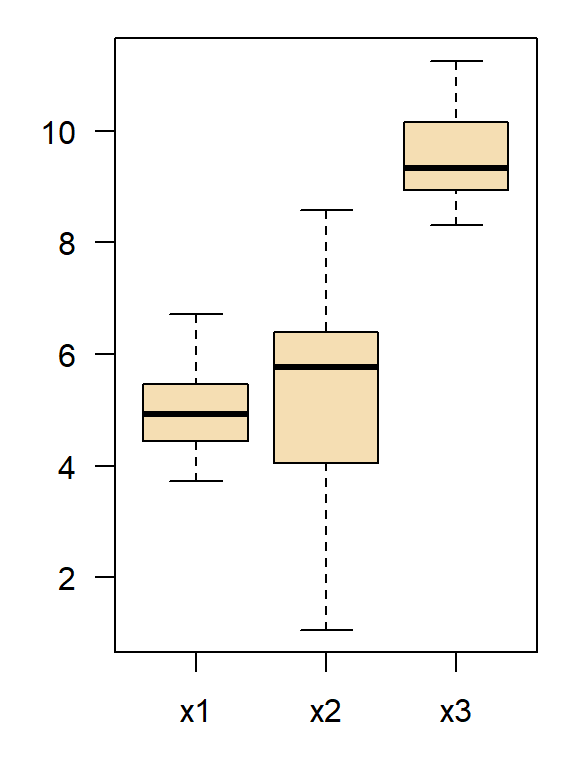
Traditionelles Vorgehen:
var.test(x, y)t.test(x, y, var.equal = TRUE)t.test(x, y) (= Welch-Test)Moderne Empfehlung (bevorzugt):
t.test(x, y)manchmal auch „t-Test für abhängige Stichproben“ genannt
Beispiele: linker Arm / rechter Arm; vorher / nachher
ist im Wesentlichen ein Einstichproben-t-Test von paarweisen Unterschieden gegen \(\mu=0\)
Reduziert den Einfluss individueller Unterschiede („Kovariate“) dank Fokussierung auf die paarweisen Unterschiede
Two Sample t-test
data: x1 and x2
t = -1.372, df = 8, p-value = 0.2073
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-4.28924 1.08924
sample estimates:
mean of x mean of y
4.0 5.6 p=0.20, nicht signifikant
Paired t-test
data: x1 and x2
t = -4, df = 4, p-value = 0.01613
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
-2.710578 -0.489422
sample estimates:
mean difference
-1.6 p=0.016, signifikant
Der gepaarte t-Test besitzt in diesem Fall eine größere Power (Trennschärfe).
Grundprinzip: Zählung der so genannten „Inversionen“ der Ränge, d.h. wie oft sich die Reihenfolge der Stichproben überschneidet
\[\begin{align*} U_A &= m \cdot n + \frac{m (m + 1)}{2} - \sum_{i=1}^m R_A \\ U_B &= m \cdot n + \frac{n (n + 1)}{2} - \sum_{i=1}^n R_B \\ U &= \min(U_A, U_B) \end{align*}\]
wilcox.exact mit Korrektur, wenn mehrfach gleiche Werte (Bindungen) vorliegen.A <- c(1, 3, 4, 5, 7)
B <- c(6, 8, 9, 10, 11)
wilcox.test(A, B) # für gepaarte Daten optionales Argument `paired = TRUE` verwenden
Wilcoxon rank sum exact test
data: A and B
W = 1, p-value = 0.01587
alternative hypothesis: true location shift is not equal to 0Mann-Whitney - Wilcoxon-Test mit Bindungskorrektur
Sei \(\xi_{obs}\) in unserem Beispiel \(4.5\), dann sei \(\Rightarrow\) \(p= 0.97\).
Wie viele Wiederholungen benötige ich?
Hängt ab von:
\[\delta=\frac{(\bar{x}_1-\bar{x}_2)}{s}\]
Je kleiner \(\alpha\), \(n\) und \(\delta\), desto größer ist der Fehler zweiter Art (\(\beta\)).
Der \(\beta\)-Fehler ist die Wahrscheinlichkeit, Effekte zu übersehen, obwohl sie vorhanden sind.
Die Trennschärfe (Power) (\(1-\beta\)) ist die Wahrscheinlichkeit, dass ein Test signifikant ist, wenn ein Effekt vorhanden ist.
Formel für den Mindeststichprobenumfang im Einstichprobenfall:
\[ n = \bigg(\frac{z_\alpha + z_{1-\beta}}{\delta}\bigg)^2 \]
qnorm) der Standardnormalverteilung für \(\alpha\) und für \(1-\beta\)Beispiel
Zweiseitiger Test mit \(\alpha=0.025\) und \(\beta=0.2\)
\(\rightarrow\) \(z_\alpha = 1.96\), \(z_\beta=0.84\), dann:
\[ n= (1.96 + 0.84)^2 \cdot 1/\delta^2 \approx 8 /\delta^2 \]
\(\delta = 1.0\cdot \sigma\) \(\qquad\Rightarrow\) n > 8
\(\delta = 0.5\cdot \sigma\) \(\qquad\Rightarrow\) n > 32
Die Trennschärfe eines t-Tests bzw. der Mindeststichprobenumfang kann mit der Funktion power.t.test() geschätzt werden:
Two-sample t test power calculation
n = 5
delta = 0.5
sd = 1
sig.level = 0.05
power = 0.1038399
alternative = two.sided
NOTE: n is number in *each* group\(\rightarrow\) ‘power’ = 0.10
Für einen schwachen Effekt von \(0.5\sigma\) wird \(n\ge 64\) in jeder Gruppe benötig:
\(\Rightarrow\) Man braucht entweder einen großen Stichprobenumfang oder einen starken Effekt.
# Grundgesamtheitsparameter
n <- 10
xmean1 <- 50; xmean2 <- 55
xsd1 <- xsd2 <- 10
alpha <- 0.05
nn <- 1000 # Anzahl an Testläufen der Simulation
a <- b <- 0 # initialisiere Zähler
for (i in 1:nn) {
# erstelle Zufallszahlen
x1 <- rnorm(n, xmean1, xsd1)
x2 <- rnorm(n, xmean2, xsd2)
# Ergebnisse des t-Tests
p <- t.test(x1,x2,var.equal = TRUE)$p.value
if (p < alpha) {
a <- a+1
} else {
b <- b+1
}
}
print(paste("a=", a, ", b=", b, ", a/n=", a/nn, ", b/n=", b/nn))Nominale Variablen
Ordinale Variablen
Metrische Skalen
Beispiel: Verteilung von Daphnien (Wasserflöhen) in den Wasserschichten eines Sees:
| Klon | Obere Schicht | Tiefe Schicht |
|---|---|---|
| A | 50 | 87 |
| B | 37 | 78 |
| C | 72 | 45 |
| Klon A | Klon B | Klon C | Summe \(s_i\) | |
|---|---|---|---|---|
| Obere Schicht | 50 | 37 | 72 | 159 |
| Untere Schicht | 87 | 78 | 45 | 210 |
| Summe \(s_j\) | 137 | 115 | 117 | \(n=369\) |
| Klon A | Klon B | Klon C | Summe \(s_i\) | |
|---|---|---|---|---|
| Obere Schicht | 59.0 | 49.6 | 50.4 | 159 |
| Untere Schicht | 78.0 | 65.4 | 66.6 | 210 |
| Summe \(s_j\) | 137 | 115 | 117 | \(n=369\) |
Teststatistik \(\hat{\chi}^2 = \sum_{i, j} \frac{(O_{ij} - E_{ij})^2}{E_{ij}}\)
Vergleich mit kritischem \(\chi^2\) aus der Tabelle mit \((n_{Zeile} - 1) \cdot (n_{Spalte} - 1)\) df.
Organisiere die Daten in einer Matrix mit 3 Zeilen (für die Klone) und 2 Spalten (für die Tiefen):
\(\rightarrow\) signifikante Korrelation zwischen den Klonen und der vertikalen Verteilung im See.
Chi-squared test for given probabilities
data: obsfreq
X-squared = 13.647, df = 8, p-value = 0.09144
Chi-squared test for given probabilities with simulated p-value (based
on 1000 replicates)
data: obsfreq
X-squared = 13.647, df = NA, p-value = 0.0969\[ T = n \omega^2 = \frac{1}{12n} + \sum_{i=1}^n \left[ \frac{2i-1}{2n}-F(x_i) \right]^2 \]
library(dgof)
obsfreq <- c(1, 1, 6, 2, 2, 5, 8, 6, 3)
## CvM-Test benötigt Einzelwerte, nicht Klassenhäufigkeiten
x <- rep(1:length(obsfreq), obsfreq)
x [1] 1 2 3 3 3 3 3 3 4 4 5 5 6 6 6 6 6 7 7 7 7 7 7 7 7 8 8 8 8 8 8 9 9 9## erstelle kumulative Verteilung mit identischer Wahrscheinlichkeit für alle Fälle
cdf <- stepfun(1:9, cumsum(c(0, rep(1/9, 9))))
cdf <- ecdf(1:9)
## führe den Test durch
cvm.test(x, cdf)
Cramer-von Mises - W2
data: x
W2 = 0.51658, p-value = 0.03665
alternative hypothesis: Two.sidedPhilosophisches Problem: Wir wollen \(H_0\) behalten!
Plausibilitätsprüfung: Vor der Analyse nachdenken!
Intrinsische Nicht-Normalität
Einige Datentypen, wie z. B. Zähldaten (z. B. Anzahl der Vorkommnisse) oder binäre Daten (z. B. Ja/Nein), sind von Natur aus nicht normalverteilt.
\(\rightarrow\) Ziel: prüft, ob eine Stichprobe aus einer Normalverteilung stammt
\(\rightarrow\) der \(p\)-Wert ist größer als 0.05, also würden wir \(H_0\) behalten und schlussfolgern, dass nichts gegen die Annahme der Normalität spricht
Die Interpretation des Shapiro-Wilk-Tests ist mit Vorsicht zu betrachten:
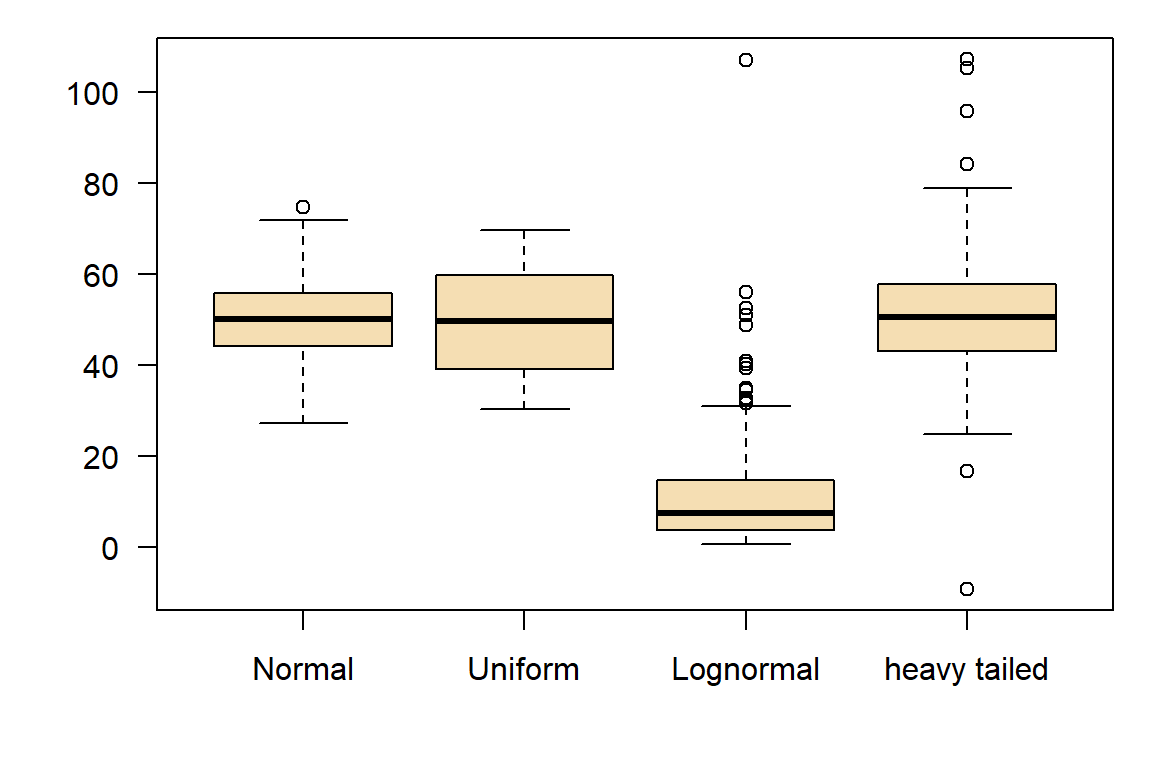
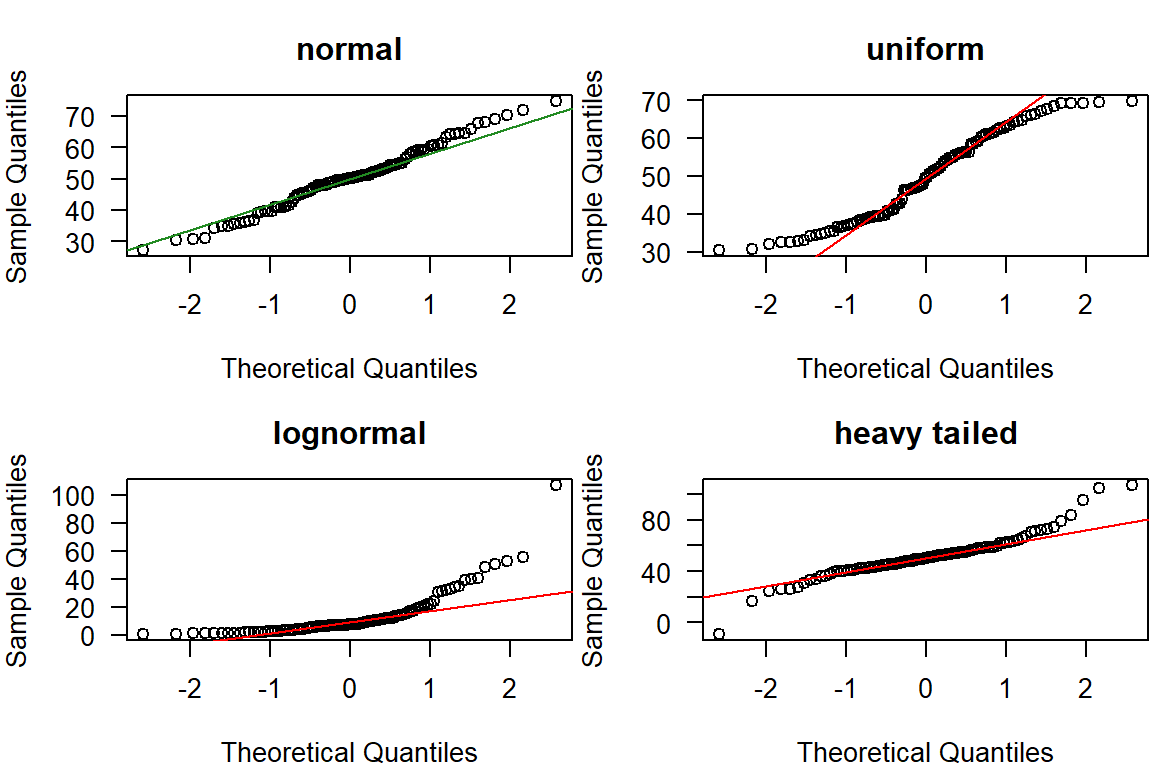
In manchen Disziplinen, z.B. in der Hydrologie, möchte man gelegentlich wissen, welcher Verteilungstyp einen Datensatz am besten beschreibt. Ein Beispiel ist die Extremwertanalyse (z.B. 100-jähriges Hochwasser), da hier das Central Limit Theorem (CLT) nicht greift.
Vorgehensweise
Transformationen für rechtsschiefe Daten
Transformationen für Zähldaten
\(\rightarrow\) besser: ein GLM der Familien Poisson oder Quasi-Poisson in Betracht ziehen
Verhältnisse und Prozentsätze
\(\rightarrow\) besser: ein GLM mit Binomialverteilung in Betracht ziehen
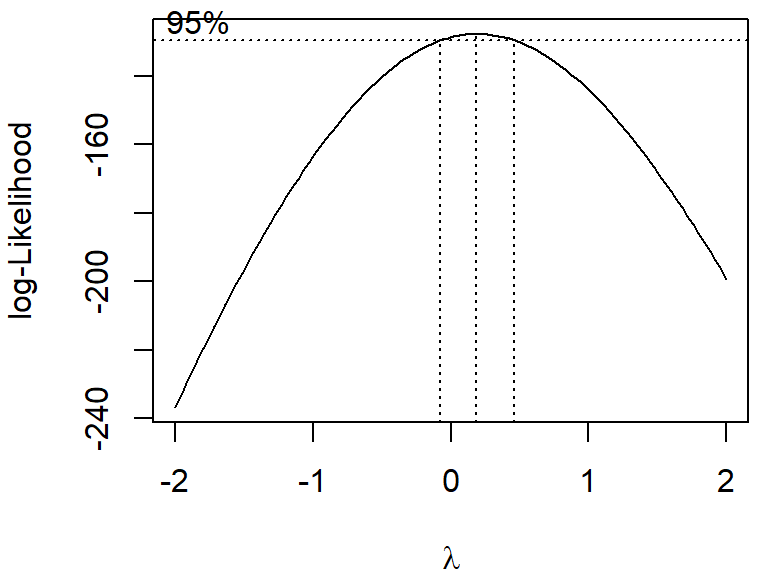
Abschätzung der optimalen Transformation aus der Klasse der Potenzen und Logarithmen:
\[ y' = \begin{cases} \frac{y^\lambda - 1}{\lambda} & \text{wenn } \lambda \neq 0 \\ \ln(y) & \text{wenn } \lambda = 0 \end{cases} \]
In vielen praktischen Fällen kann man statt \(\frac{y^\lambda - 1}{\lambda}\) vereinfacht \(y^\lambda\) verwenden.
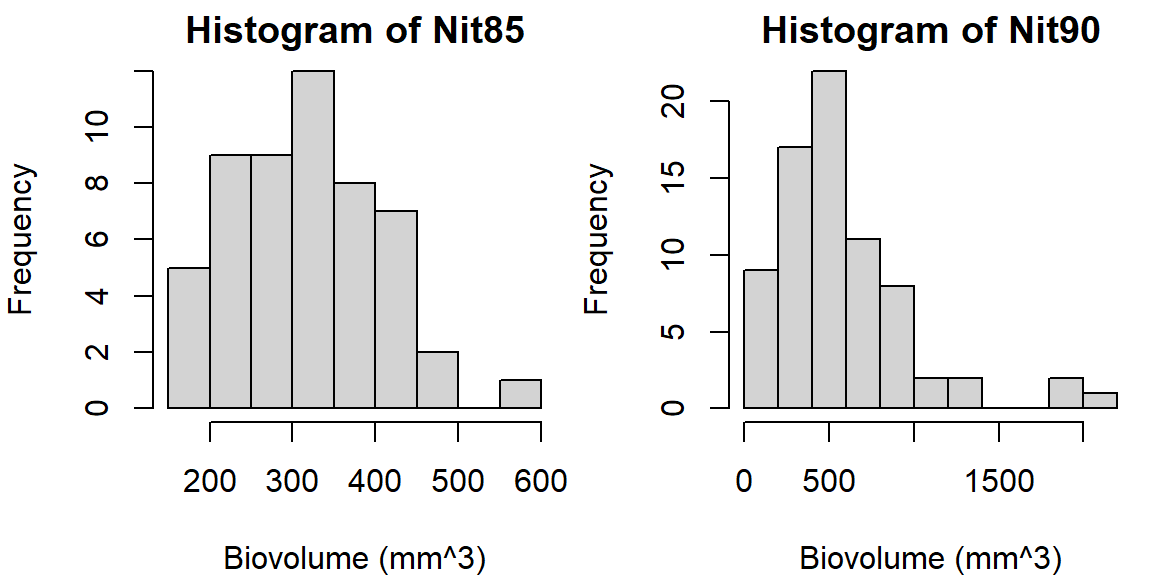
boxcox ist eine sogenannte „Modellformel“ oder das Ergebnis eines linearen Modells (lm)~ 1).biovol ~ groupHäufigkeiten von nominalen Variablen
⇒ Abhängigkeit zwischen Pflanzenart und Bodentyp
(siehe oben)
Ordinale Variablen
\(\rightarrow\) Rangzahlen
Metrische Skalen
Varianz
\[ s^2_x = \frac{\text{Quadratsumme}}{\text{Freiheitsgrade}}=\frac{\sum_{i=1}^n (x_i-\bar{x})^2}{n-1} \]
Kovarianz
\[ q_{x,y} = \frac{\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})}{n-1} \]
Korrelation: skaliert auf \((-1, +1)\)
\[ r_{x,y} = \frac{q_{x,y}}{s_x \cdot s_y} \]
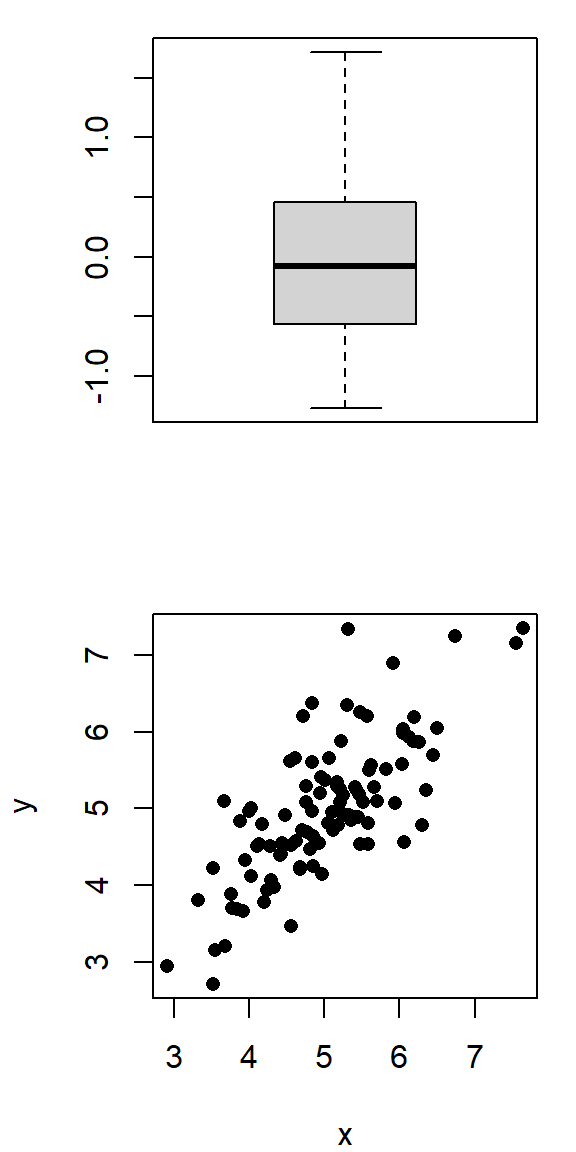
\[ r_p=\frac{\sum{(x_i-\bar{x}) (y_i-\bar{y})}} {\sqrt{\sum(x_i-\bar{x})^2\sum(y_i-\bar{y})^2}} \]
Oder:
\[
r_p=\frac {\sum xy - \sum y \sum y / n}
{\sqrt{(\sum x^2-(\sum x)^2/n)(\sum y^2-(\sum y)^2/n)}}
\]
Wertebereich: \(-1 \le r_p \le +1\)
| \(0\) | keine gegenseitige Abhängigkeit |
| \(+1 \,\text{or}\,-1\) | strikt positive bzw. negative Abhängigkeit |
| \(0 < |r_p| < 1\) | positive bzw. negative Abhängigkeit |
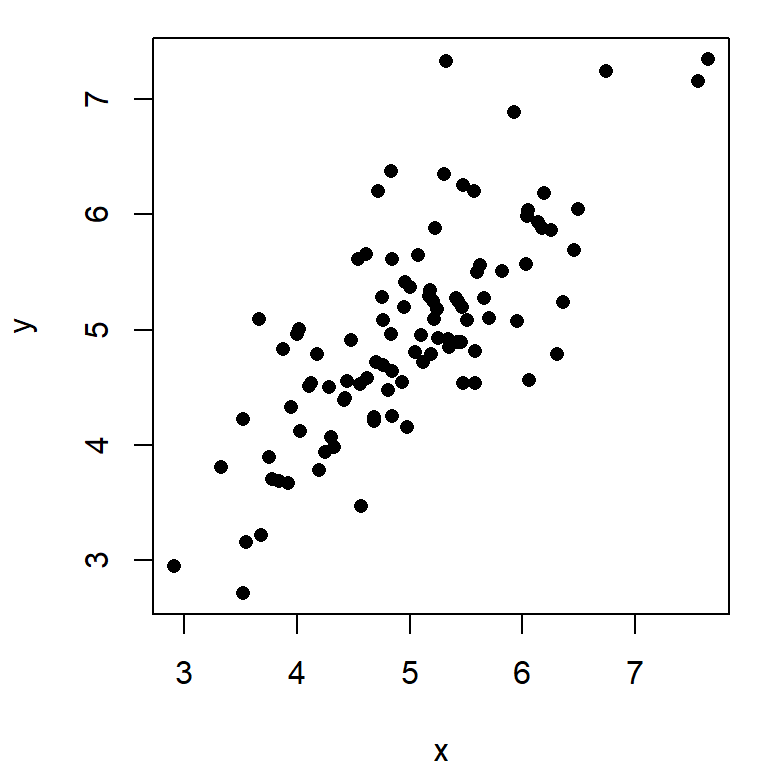
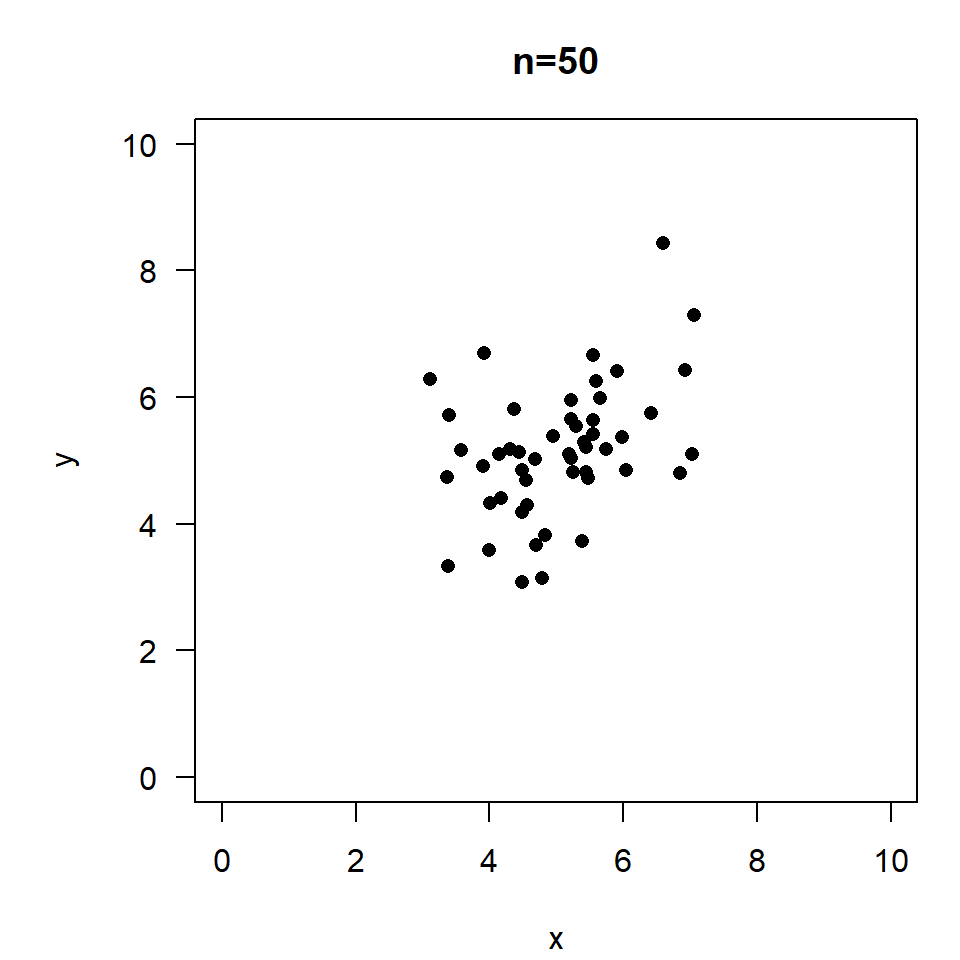
\(r=0.4, \quad p=0.0039\)
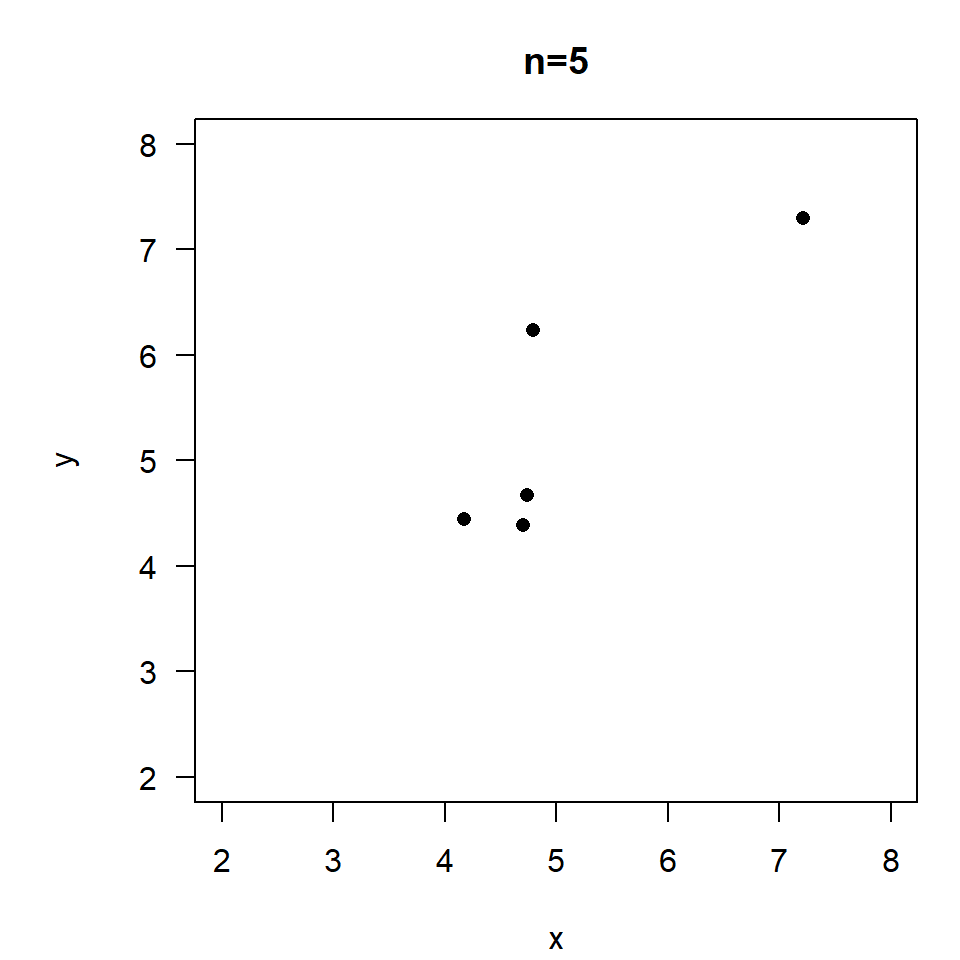
\(r=0.85, \quad p=0.07\)
\[ \hat{t}_{\alpha/2;n-2} =\frac{|r_p|\sqrt{n-2}}{\sqrt{1-r^2_p}} \]
\(t=0.829 \cdot \sqrt{1000-2}/\sqrt{1-0.829^2}=46.86, df=998\)
Schnelltest: kritische Werte für \(r_p\)
| \(n\) | d.f. | \(t\) | \(r_{krit}\) |
| 3 | 1 | 12.706 | 0.997 |
| 5 | 3 | 3.182 | 0.878 |
| 10 | 8 | 2.306 | 0.633 |
| 20 | 18 | 2.101 | 0.445 |
| 50 | 48 | 2.011 | 0.280 |
| 100 | 98 | 1.984 | 0.197 |
| 1000 | 998 | 1.962 | 0.062 |
\[ r_s=1-\frac{6 \sum d^2_i}{n(n^2-1)} \]
für \(10 \leq n\) \(\rightarrow\) \(t\)-Verteilung
\[ \hat{t}_{1-\frac{\alpha}{2};n-2} =\frac{|r_s|}{\sqrt{1-r^2_S}} \sqrt{n-2} \]
| \(x\) | \(y\) | \(R_x\) | \(R_y\) | \(d\) | \(d^2\) |
|---|---|---|---|---|---|
| 1 | 2.7 | 1 | 1 | 0 | 0 |
| 2 | 7.4 | 2 | 2 | 0 | 0 |
| 3 | 20.1 | 3 | 3 | 0 | 0 |
| 4 | 500.0 | 4 | 5 | -1 | 1 |
| 5 | 148.4 | 5 | 4 | +1 | 1 |
| 2 | |||||
\[ r_s=1-\frac{6 \cdot 2}{5\cdot (25-1)}=1-\frac{12}{120}=0.9 \]
Zum Vergleich: \(r_p=0.58\)
Vorteile
Nachteile:
Fazit: \(r_s\) ist dennoch sehr empfehlenswert!
Pearson's product-moment correlation
data: x and y
t = 7.969, df = 4, p-value = 0.001344
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.7439930 0.9968284
sample estimates:
cor
0.9699203 Wenn Linearität oder Normalität der Residuen zweifelhaft sind, verwende eine Rangkorrelation
Multiple Korrelation
Empfehlung: