| Zahl | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Häufigkeit | 0 | 1 | 5 | 5 | 6 | 4 | 12 | 3 | 3 |
04-Wahrscheinlichkeitsverteilungen
Angewandte Statistik – Ein Praxiskurs
2025-11-12
Was ist deine Lieblingszahl?
In einem Experiment im Hörsaal wurden die Studierenden eines internationalen Kurses nach ihrer Lieblingszahl von 1 bis 9 gefragt.
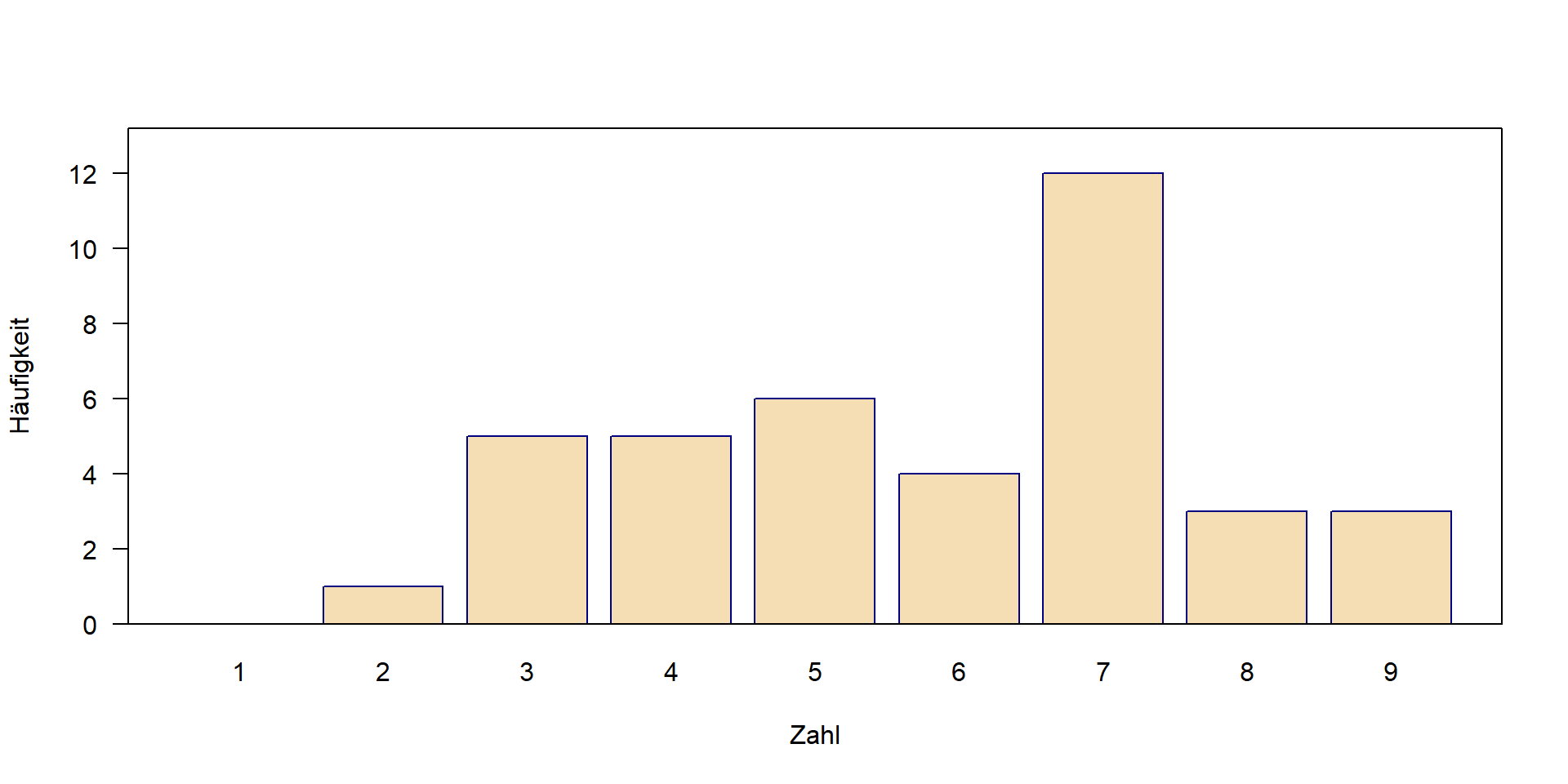
Die resultierende Verteilung ist:
- empirisch: Daten aus einem Experiment
- diskret: nur diskrete Zahlen (1, 2, 3 …, 9) möglich, keine Brüche
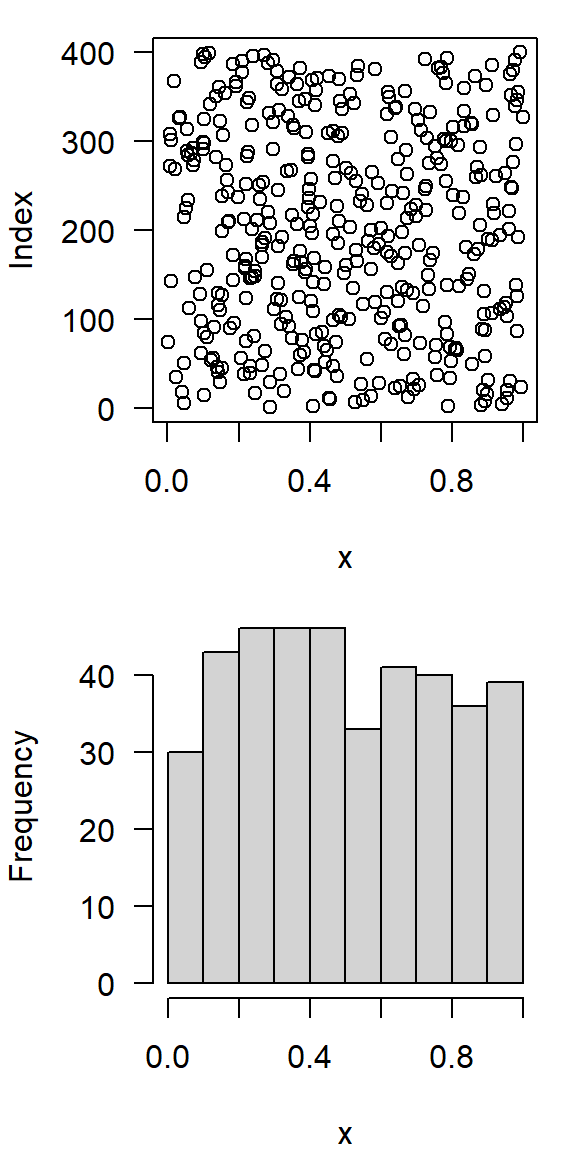
Kontinuierliche Gleichverteilung \(\mathbf{U}(0, 1)\)
- gleiche Wahrscheinlichkeit des Auftretens in einem bestimmten Intervall
- z.B. \([0, 1]\)
- in R:
runif, random, uniform
runif(10) [1] 0.829975819 0.082188891 0.002092706 0.392128511 0.390446015 0.363470901
[7] 0.081870791 0.116082502 0.296399114 0.130358771
- Klassenbildung (Binning): Einteilung der Werte in Klassen
Dichtefunktion von \(\mathbf{U}(x_{min}, x_{max})\)
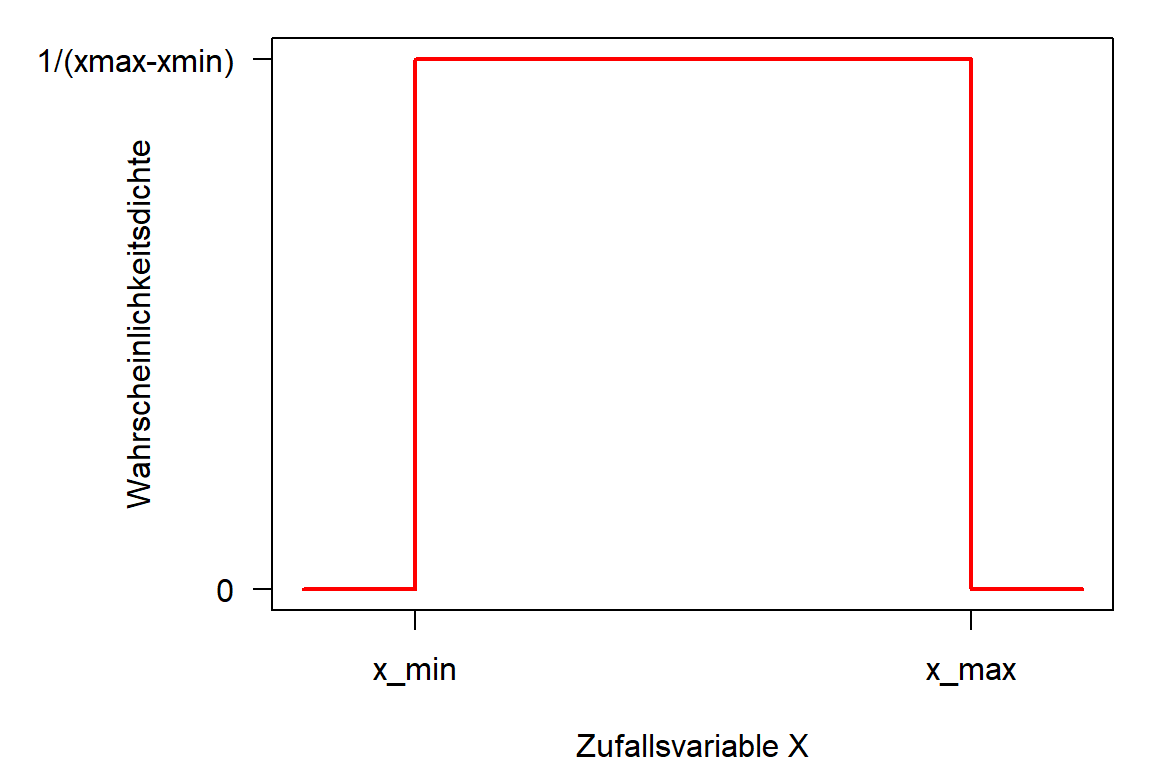
- Dichte \(f(X)\), manchmal abgekürzt als „pdf“ (probability density function):
\[ f(x) = \begin{cases} \frac{1}{x_{max}-x_{min}} & \text{für } x \in [x_{min},x_{max}] \\ 0 & \text{sonst} \end{cases} \]
- Fläche unter der Kurve (d. h. das Integral) = 1,0
- 100% der Ereignisse liegen zwischen \(-\infty\) und \(+\infty\)
und für \(\mathbf{U}(x_{min}, x_{max})\) im Intervall \([x_{min}, y_{max}]\)
Kumulative Verteilungsfunktion von \(\mathbf{U}(x_{min}, x_{max})\)
Die cdf (cumulative distribution function) ist das Integral der Dichtefunktion:
\[ F(x) =\int_{-\infty}^{x} f(x) dx \] Die Gesamtfläche (Gesamtwahrscheinlichkeit) ist \(1.0\):
\[ F(x) =\int_{-\infty}^{+\infty} f(x) dx = 1 \]
Für die Verteilungsfunktion der Gleichverteilung gilt somit:
\[ F(x) = \begin{cases} 0 & \text{für } x < x_{min} \\ \frac{x-x_{min}}{x_{max}-x_{min}} & \text{für } x \in [x_{min},x_{max}] \\ 1 & \text{für } x > x_{max} \end{cases} \]
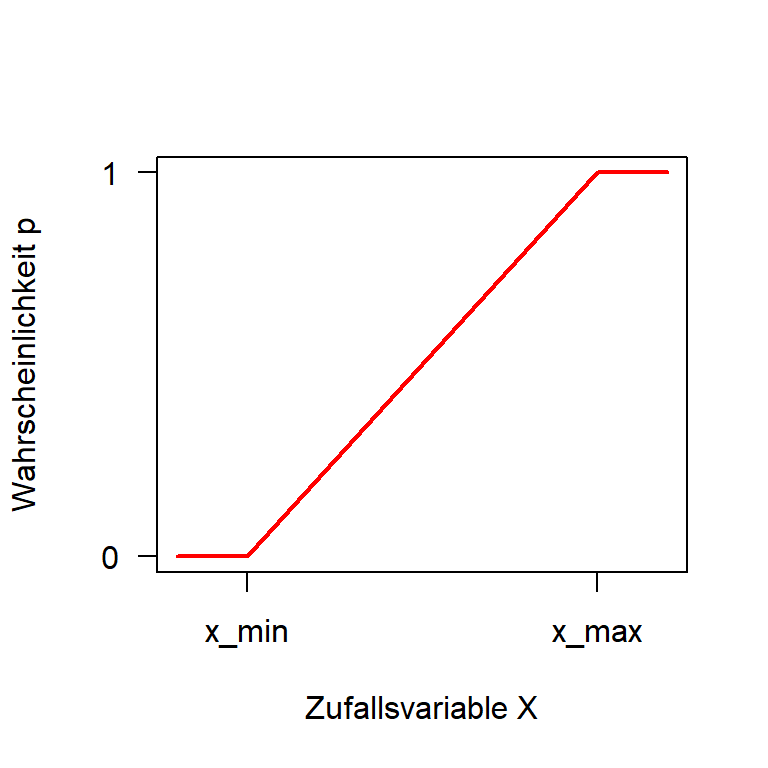
Quantilfunktion
… die Umkehrung der kumulativen Verteilungsfunktion.
Kumulative Verteilungsfunktion
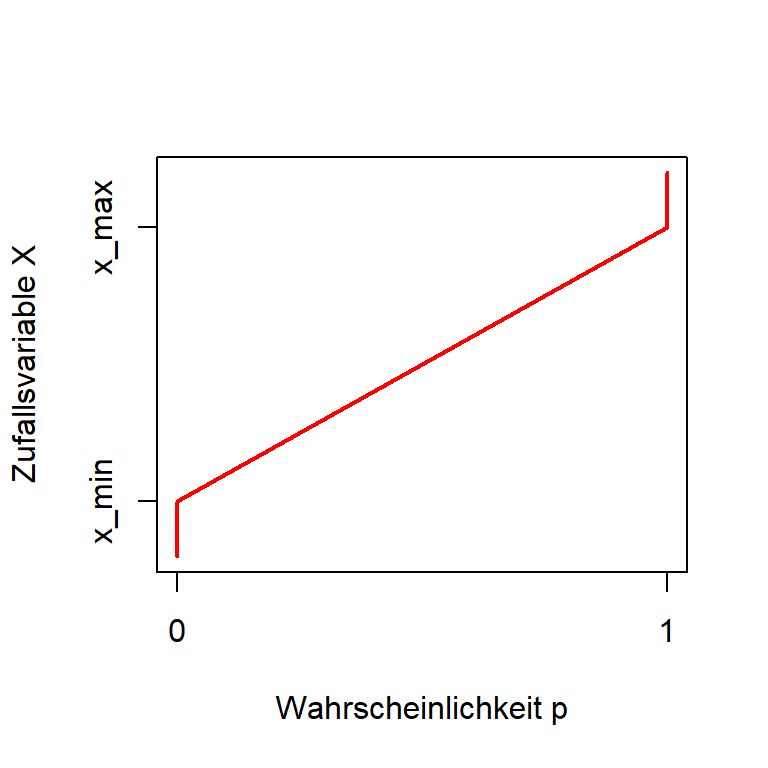
Quantilsfunktion
Beispiel: In welchem Bereich kann man 95% einer Gleichverteilung \(\mathbf{U}(40,60)\) finden?
Zusammenfassung: Gleichverteilung
Die Normalverteilung \(\mathbf{N}(\mu, \sigma)\)
- von großer theoretischer Bedeutung aufgrund des zentralen Grenzwertsatzes (ZGWS / central limit theorem CLT)
- ergibt sich aus der Addition einer großen Anzahl von Zufallswerten gleicher Größenordnung.
Die Dichtefunktion der Normalverteilung ist eine mathematische Schönheit.
\[ f(x) = \frac{1}{\sigma\sqrt{2\pi}} \, \mathrm{e}^{-\frac{(x-\mu)^2}{2 \sigma^2}} \]
C.F. Gauß, Gauß-Kurve und Formel auf einer deutschen DM-Banknote von 1991–2001 (Wikipedia, CC0)
Der zentrale Grenzwertsatz (CLT)
Die Summe einer großen Anzahl \(n\) unabhängiger und identisch verteilter Zufallswerte konvergiert gegen eine Normalverteilung, unabhängig vom Typ der ursprünglichen Verteilung.
Ein Simulationsexperiment
- Erstelle eine Matrix mit 100 Zeilen und 25 Spalten von gleichverteilten Zufallszahlen
- Berechne die Zeilensummen
par(mfrow=c(2, 1), las=1)
set.seed(42)
x <- matrix(runif(25 * 100), ncol = 25)
# View(x) # uncomment this to show the matrix
x_sums <- rowSums(x)
hist(x)
hist(x_sums)
\(\rightarrow\) Zeilensummen sind annähernd normalverteilt
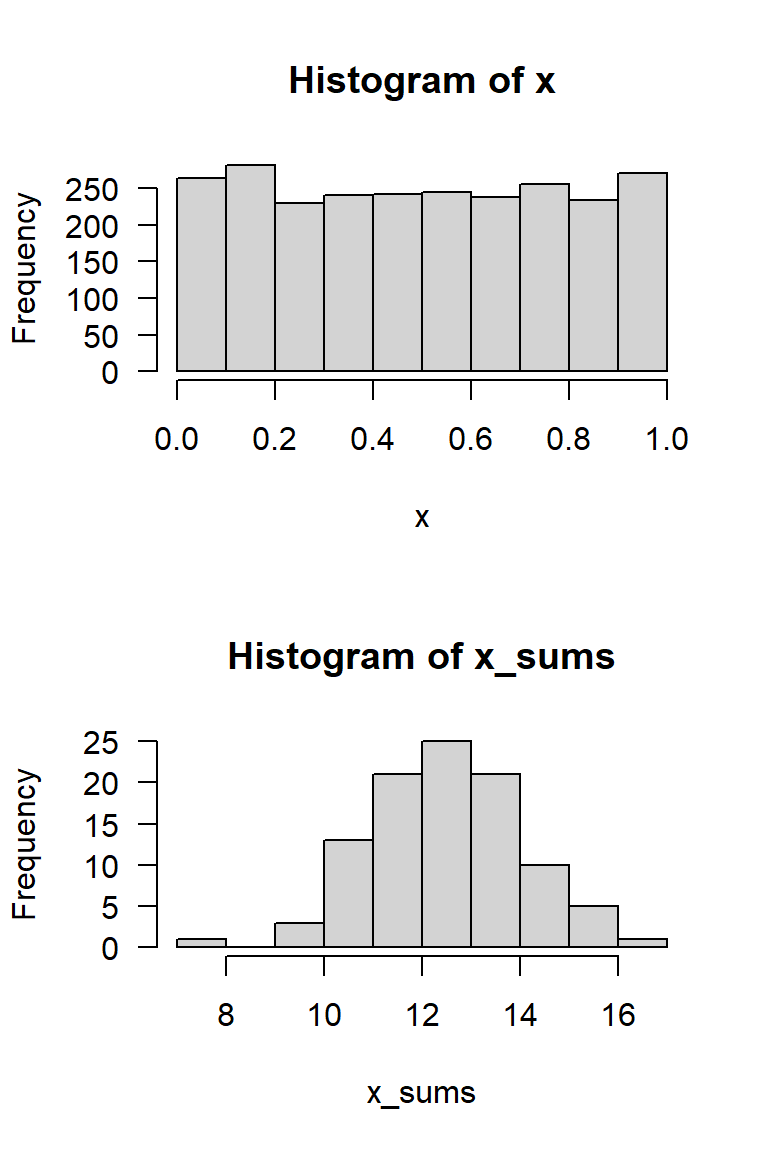
Zufallszahlen und Dichtefunktion
Dichte und Quantile der Standardnormalverteilung
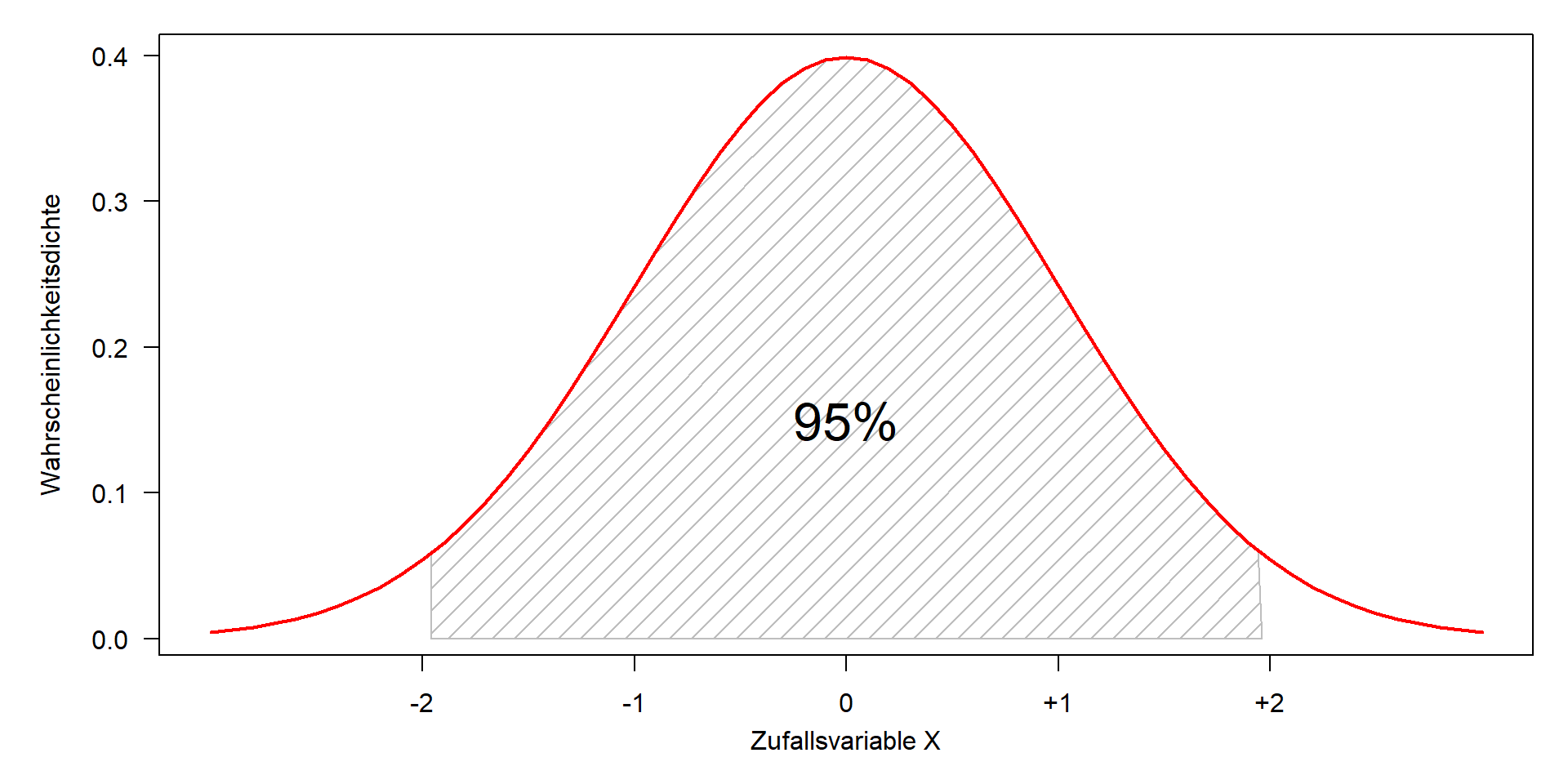
- Theoretisch liegen 50% der Werte unter und 50% über dem Mittelwert
- 95% liegen ungefähr zwischen \(\pm 2 \sigma\)
Dichte und Quantile der Standardnormalverteilung
Kumulative Verteilungsfunktion und Quantilfunktion
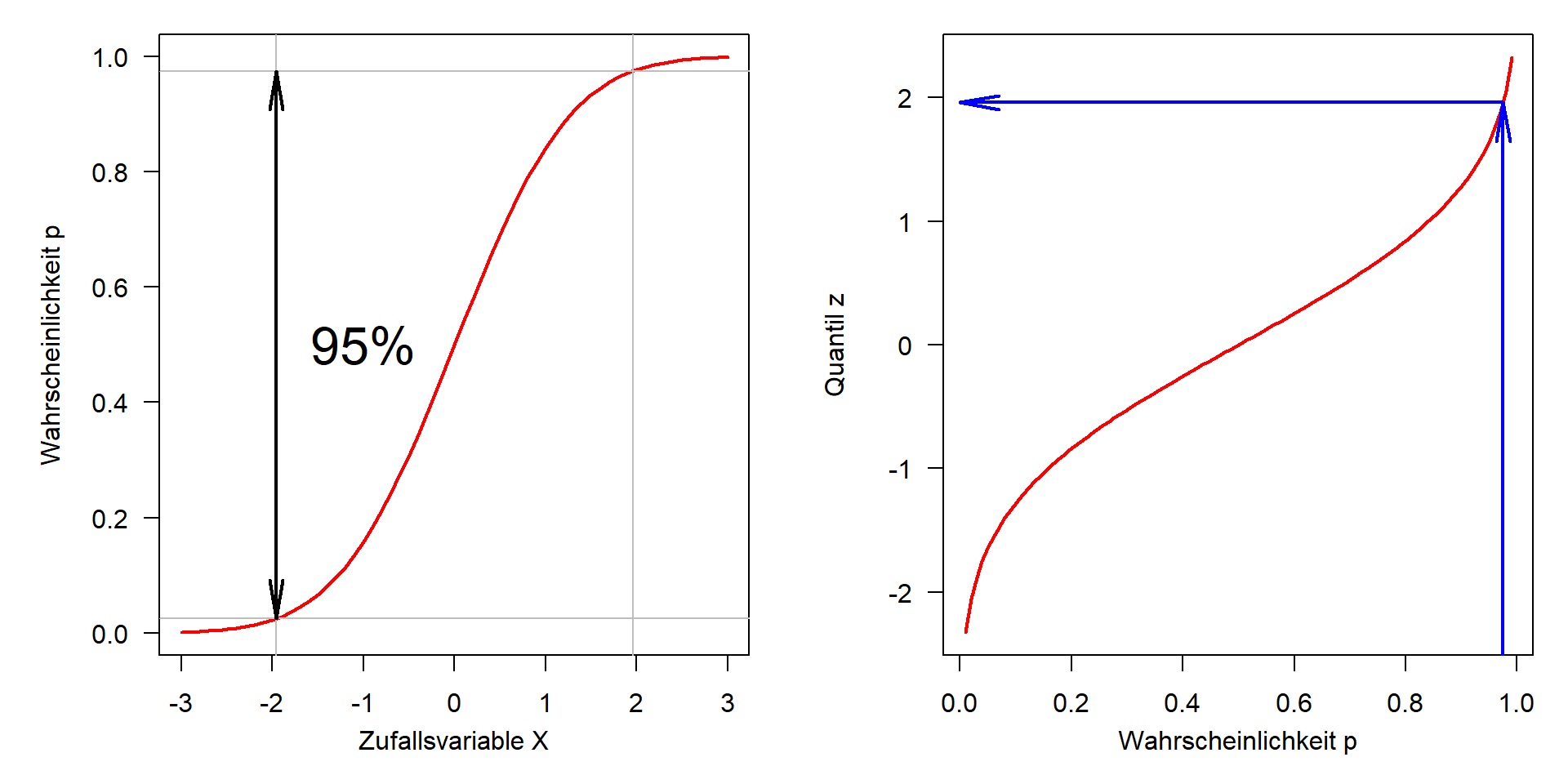
| Quantil | 1 | 1.64 | 1.96 | 2.0 | 2.33 | 2.57 | 3 | \(\mu \pm z\cdot \sigma\) |
|---|---|---|---|---|---|---|---|---|
| einseitig | 0.95 | 0.975 | 0.977 | 0.99 | 0.995 | 0.9986 | \(1-\alpha\) | |
| zweiseitig | 0.68 | 0.90 | 0.95 | 0.955 | 0.98 | 0.99 | 0.997 | \(1-\alpha/2\) |
Standardnormalverteilung, Skalierung und Verschiebung
- \(\mu\) ist der Verschiebungsparameter, der die gesamte glockenförmige Kurve entlang der \(x\)-Achse verschiebt.
- \(\sigma\) ist der Skalierungsparameter, der die Kurve in Richtung \(x\) streckt oder staucht.
Standardisierung (\(z\)-Transformation)
Jede Normalverteilung kann skaliert und verschoben werden, um eine Standardnormalverteilung mit \(\mu=0, \sigma=1\) zu bilden.
Normalverteilung
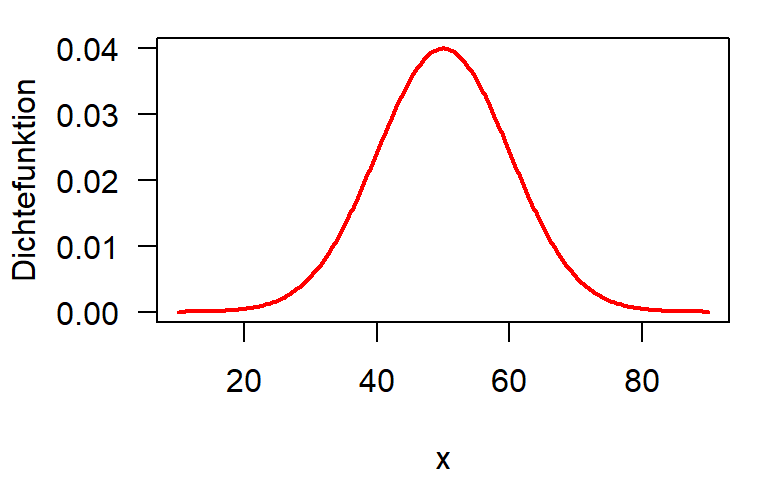
\[ f(x) = \frac{1}{\sigma\sqrt{2\pi}} \, \mathrm{e}^{-\frac{(x-\mu)^2}{2 \sigma^2}} \]
\[
z = \frac{x-\mu}{\sigma}
\] \(\longrightarrow\) \(\longrightarrow\) \(\longrightarrow\)
Standardnormalverteilung
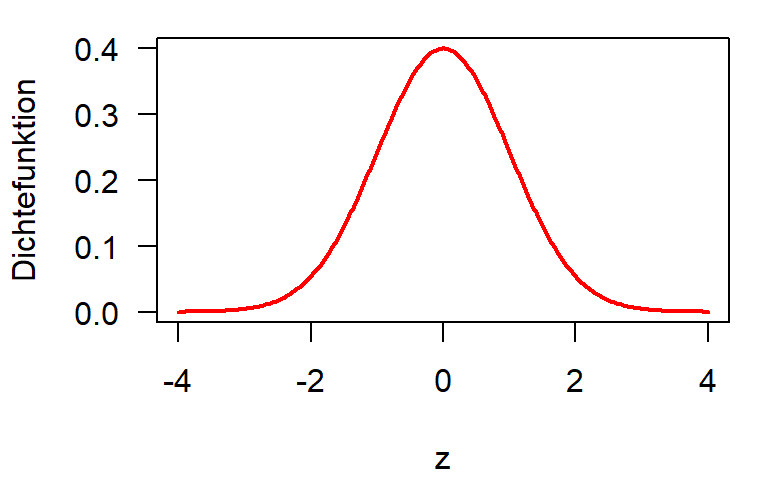
\[ f(x) = \frac{1}{\sqrt{2\pi}} \, \mathrm{e}^{-\frac{1}{2}x^2} \]
t-Verteilung \(\mathbf{t}(x, df)\)
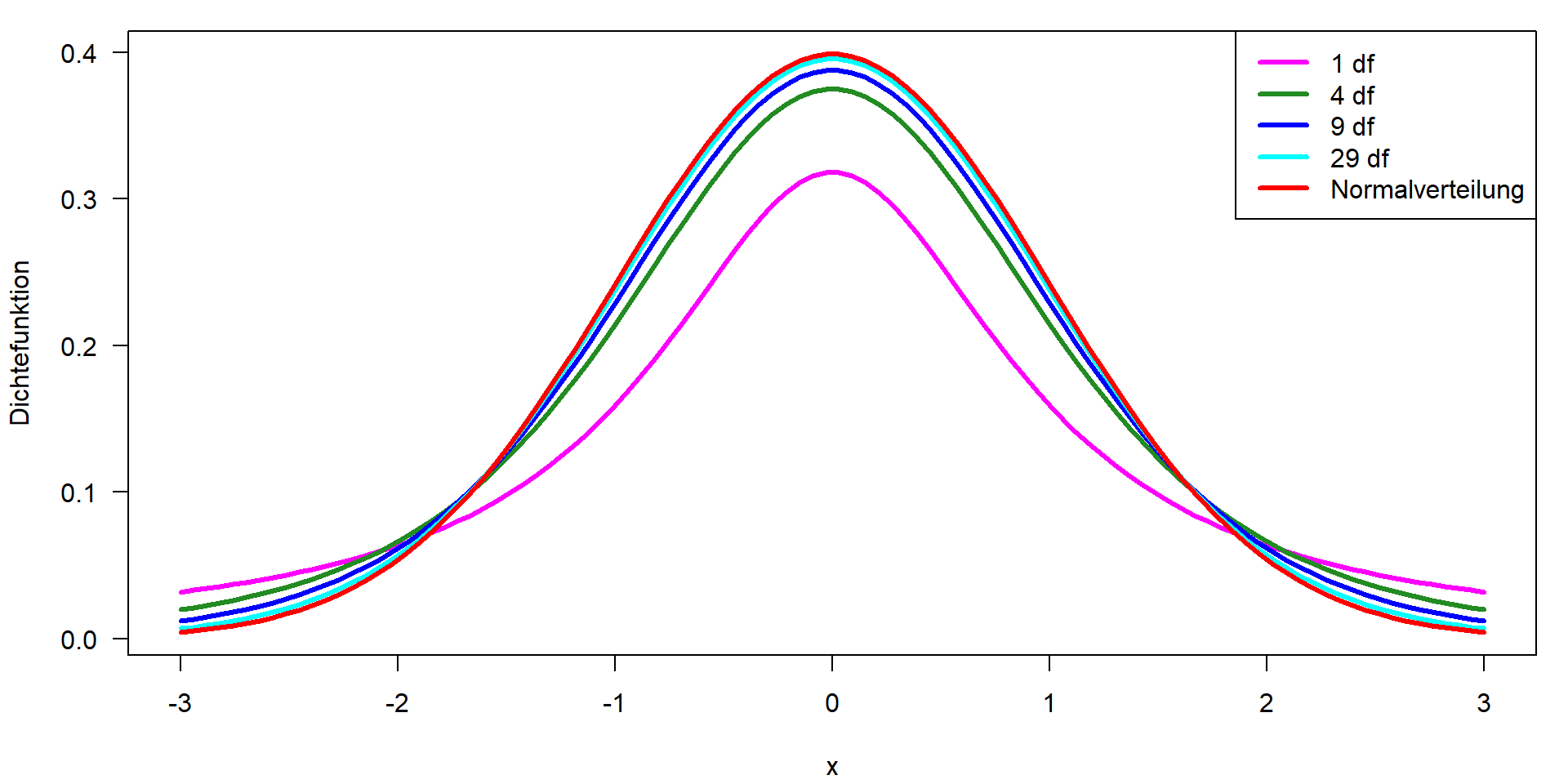
- zusätzlicher Parameter „Freiheitsgrade“ (df)
- wird für Konfidenzintervalle und statistische Tests verwendet
- konvergiert gegen Normalverteilung für \(df \rightarrow \infty\)
Abhängigkeit des t-Wertes von der Anzahl der df
| df | 1.00 | 4.00 | 9.00 | 19.00 | 29.00 | 99.00 | 999.00 |
| t | 12.71 | 2.78 | 2.26 | 2.09 | 2.05 | 1.98 | 1.96 |
Logarithmische Normalverteilung (Lognormal)
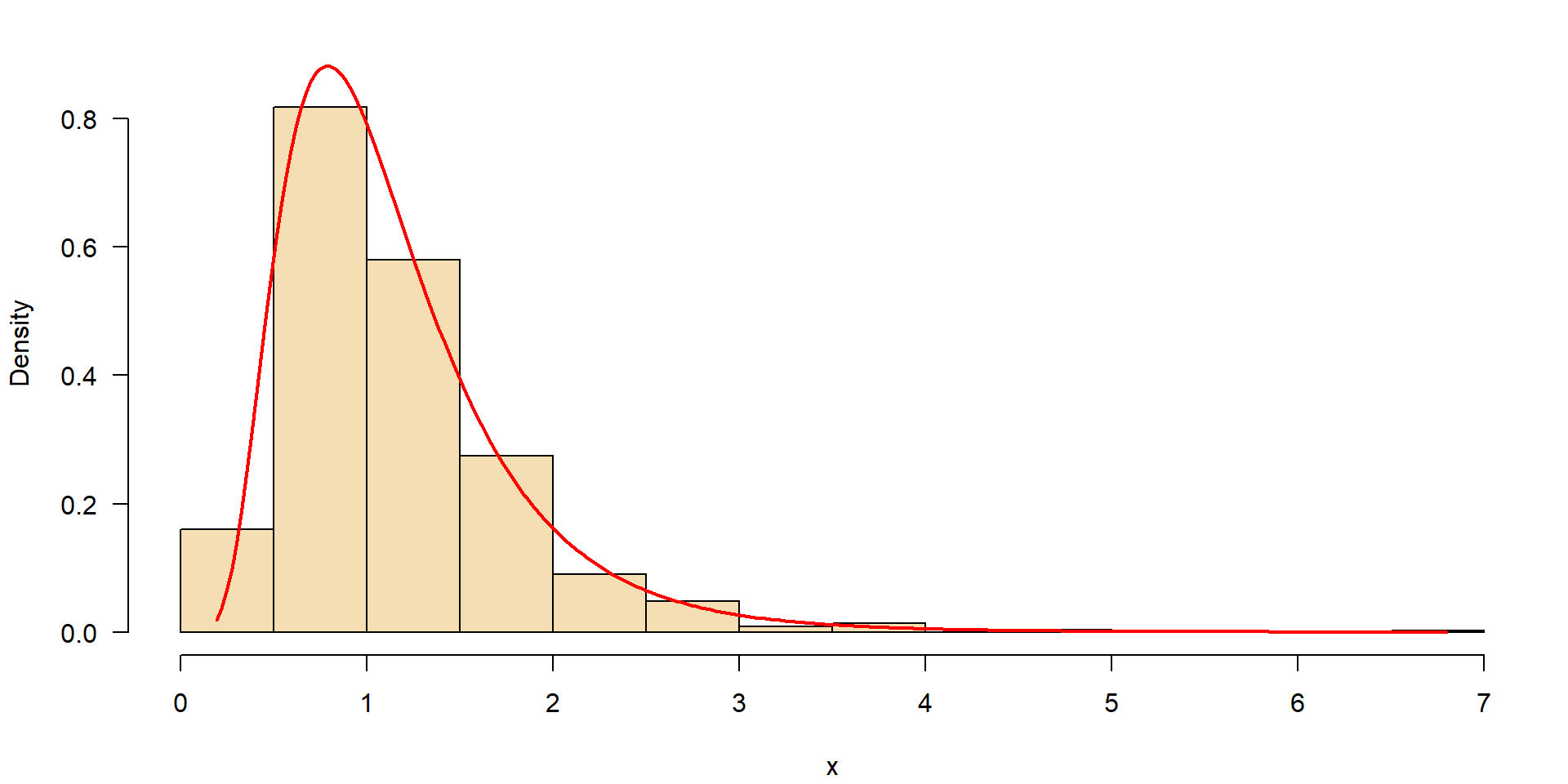
- Viele Prozesse in der Natur folgen nicht einer Normalverteilung.
- begrenzt durch Null auf der linken Seite
- große Extremwerte auf der rechten Seite
Beispiele: Abfluss von Flüssen, Nährstoffkonzentrationen, Algenbiomasse in einem See
Elternverteilung der Lognormalverteilung
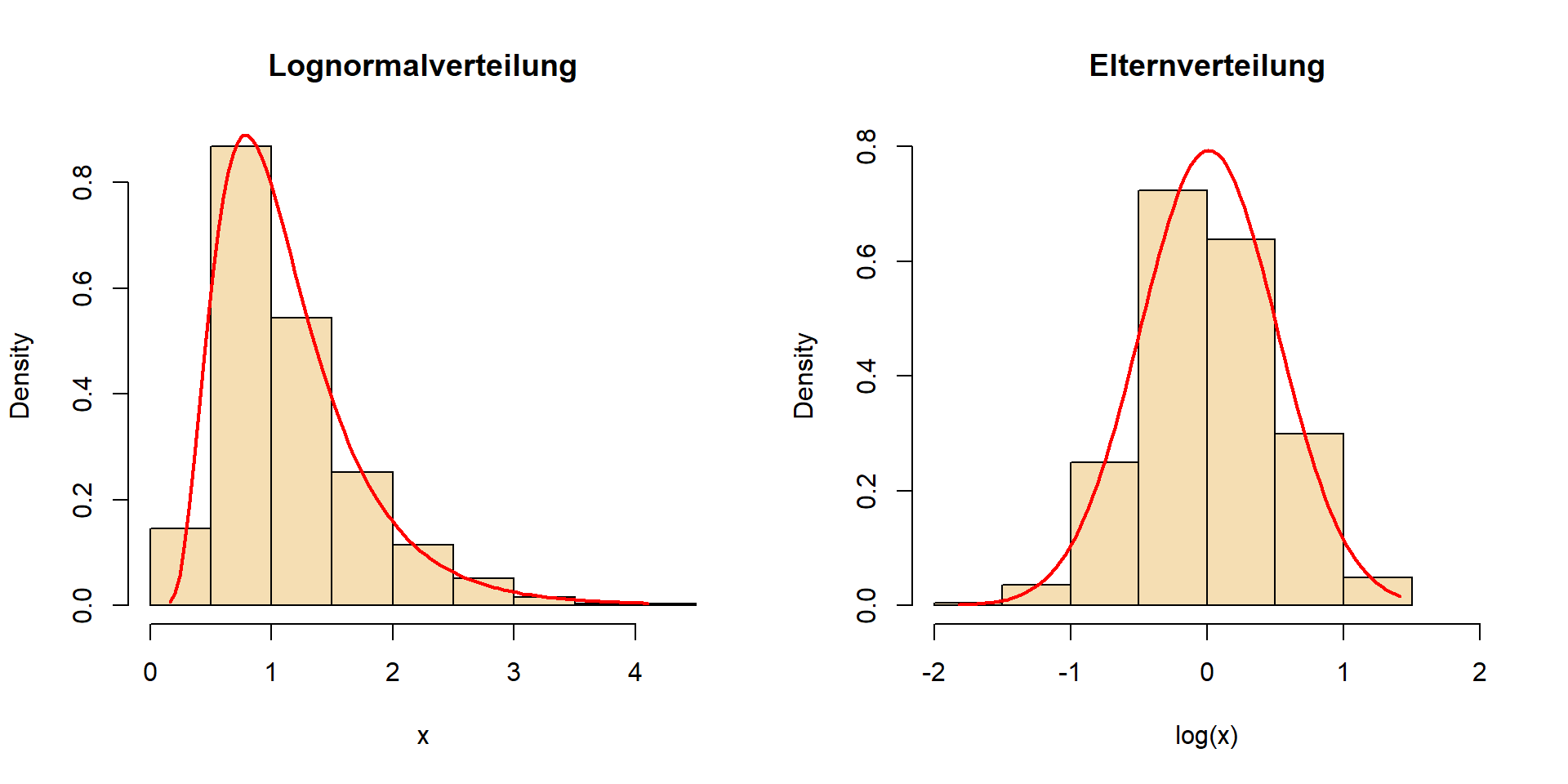
- Logarithmus von Werten einer Lognormalverteilung \(\rightarrow\) Eltern-Normalverteilung.
- Die Lognormalverteilung wird durch die Parameter der log-transformierten Daten \(\bar{x}_L\) und \(s_L\) beschrieben
- der Antilog von \(\bar{x}_L\) ist das geometrische Mittel
Binomialverteilung
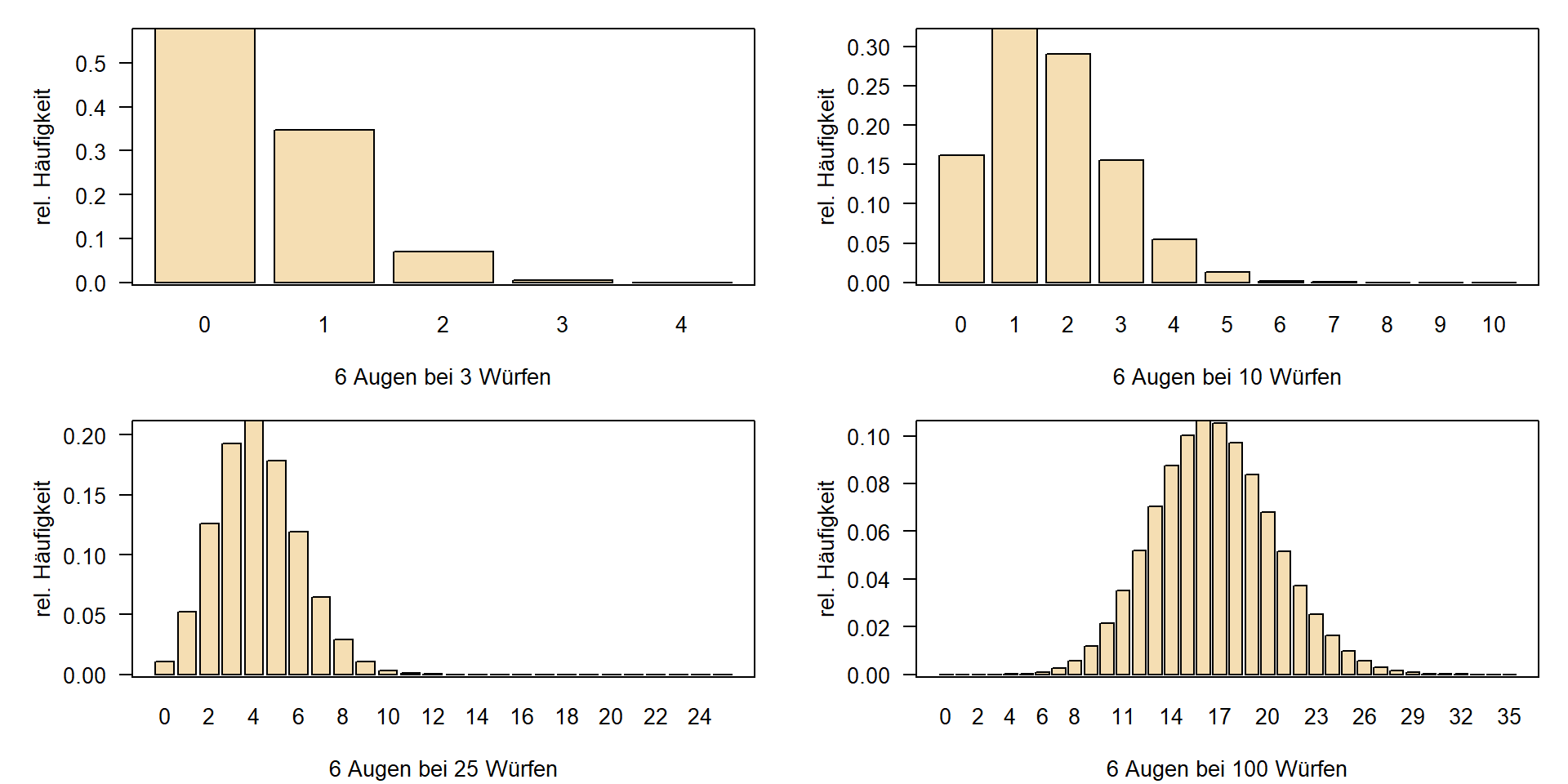
- Anzahl der erfolgreichen Versuche aus \(n\) Gesamtversuchen mit Erfolgswahrscheinlichkeit \(p\).
- Wie viele 6en mit Wahrscheinlichkeit \(1/6\) in 3 Versuchen?
- Medizin, Toxikologie, Vergleich von Prozentzahlen
- Ähnlich, aber ohne zurücklegen: Hypergeometrische Verteilung im Lotto
Poisson-Verteilung
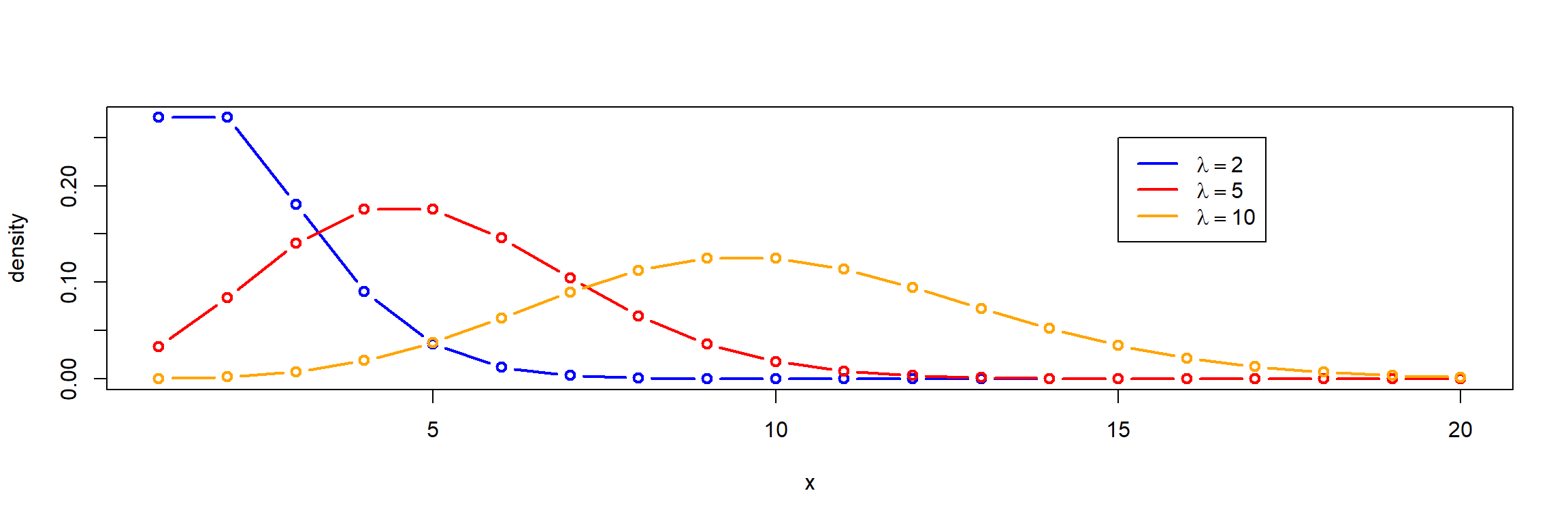
- Verteilung von seltenen Ereignissen, eine diskrete Verteilung
- Mittelwert und Varianz sind gleich (\(\mu = \sigma^2\)), daraus ergibt sich der Parameter „lambda“ (\(\lambda\))
- Beispiele: Bakterienzählung auf einem Raster, Warteschlangen, Ausfallmodelle
Quasi-Poisson, wenn \(\mu \neq \sigma^2\)
- Wenn \(s^2 > \bar{x}\): Überdispersion
- wenn \(s^2 < \bar{x}\): Unterdispersion
Konfidenzintervall
– hängt nur von \(\lambda\) bzw. der Anzahl der gezählten Einheiten (\(k\)) ab
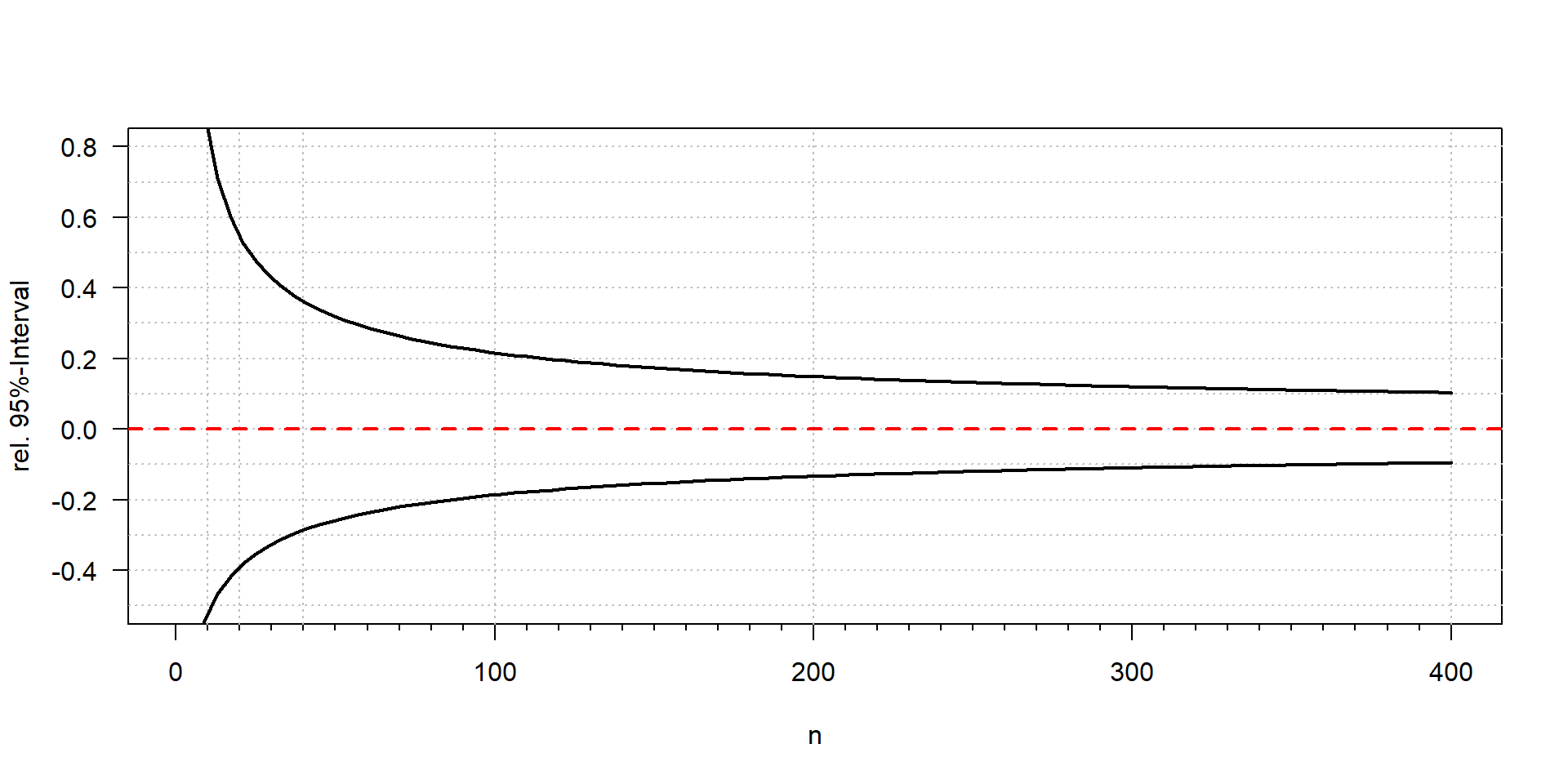
Typischer Fehler bei einer Zellzählung: 95% Konfidenzintervall
| Anzahl | 2 | 3 | 5 | 10 | 50 | 100 | 200 | 400 | 1000 |
| von | 0 | 1 | 2 | 5 | 37 | 81 | 173 | 362 | 939 |
| bis | 7 | 9 | 12 | 18 | 66 | 122 | 230 | 441 | 1064 |
Zur Erinnerung: Der zentrale Grenzwertsatz (ZGWS)
Die Summen einer großen Anzahl \(n\) unabhängiger und identisch verteilter Zufallswerte konvergieren gegen eine Normalverteilung, unabhängig vom Typ der ursprünglichen Verteilung.
- Wir können Methoden für eine Normalverteilung auch bei Abweichungen von der NV anwenden:
- wenn wir einen großen Datensatz haben
- wenn die ursprüngliche Verteilung nicht „zu schief“ ist
- Die erforderliche Zahl \(n\) hängt von der Schiefe der ursprünglichen Verteilung ab.
Grund: Methoden wie t-Test oder ANOVA basieren auf Mittelwerten.
Extremwerte in Boxplots
- Extremwerte außerhalb der Whiskers, wenn sie mehr als das 1,5-fache der Breite der Interquartilsbox von den Boxgrenzen entfernt sind.
- Manchmal auch „Ausreißer“ genannt.
- Ich bevorzuge den Begriff „Extremwert“, da es sich um regelmäßige Beobachtungen aus einer schiefen oder einer ‘heavy tailed’ Verteilung handeln kann.
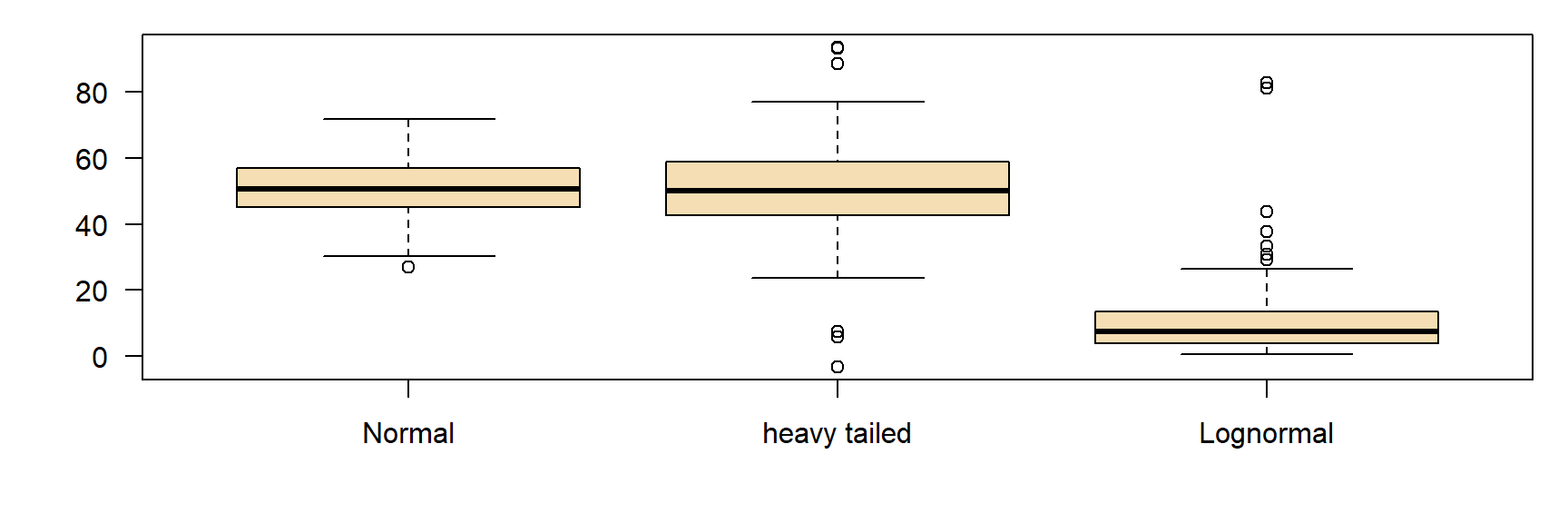
Beispiel
par(mfrow=c(1, 3), las=1)
elbe <- read.csv("https://tpetzoldt.github.io/datasets/data/elbe.csv")
discharge <- elbe$discharge
boxplot(discharge, main="Boxplot des Abflusses")
hist(discharge)
hist(log(discharge - 70))
Abflussdaten der Elbe in Dresden in \(\mathrm m^3 s^{-1}\), Datenquelle: Bundesanstalt für Gewässerkunde (BFG), siehe Nutzungshinweise.
- Links: große Anzahl von Extremwerten, sind das Ausreißer?
- Mitte: Verteilung ist rechtsschief.
- Rechts: Transformation (3-parametrische Lognormalverteilung)
\(\rightarrow\) symmetrische Verteilung, keine Ausreißer!